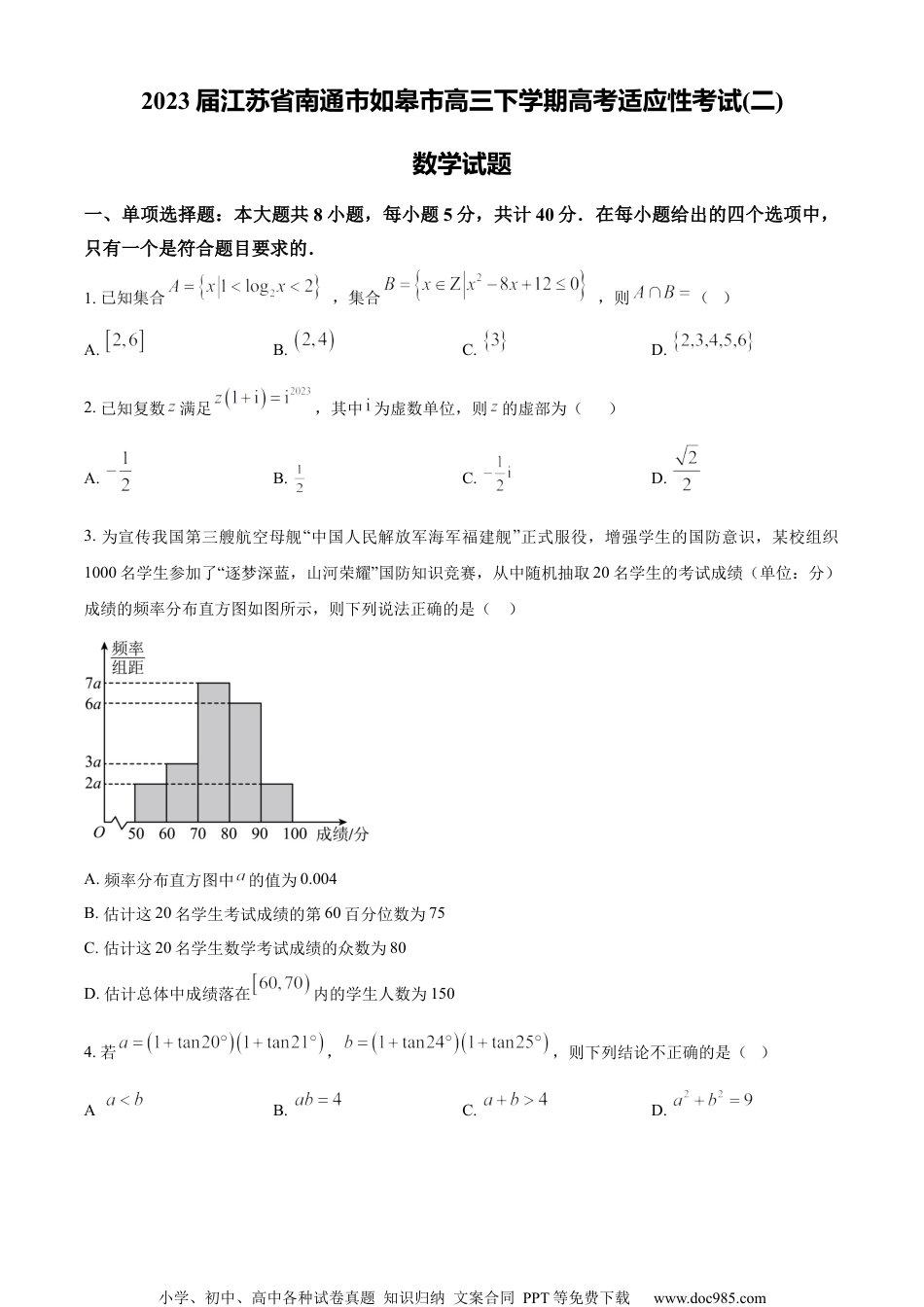
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2023届江苏省南通市如皋市高三下学期高考适应性考试(二)数学试题一、单项选择题：本大题共8小题，每小题5分，共计40分．在每小题给出的四个选项中，只有一个是符合题目要求的．1.已知集合，集合，则（）A.B.C.D.2.已知复数满足，其中为虚数单位，则的虚部为（）A.B.C.D.3.为宣传我国第三艘航空母舰“中国人民解放军海军福建舰”正式服役，增强学生的国防意识，某校组织1000名学生参加了“逐梦深蓝，山河荣耀”国防知识竞赛，从中随机抽取20名学生的考试成绩（单位：分）成绩的频率分布直方图如图所示，则下列说法正确的是（）A.频率分布直方图中的值为0.004B.估计这20名学生考试成绩的第60百分位数为75C.估计这20名学生数学考试成绩的众数为80D.估计总体中成绩落在内的学生人数为1504.若，，则下列结论不正确的是（）A.B.C.D.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com5.已知圆的方程为，直线为圆的切线，记两点到直线的距离分别为，动点满足，，则动点的轨迹方程为（）A.B.C.D.6.已知，，，则（）A.B.C.D.7.已知圆台两个底面圆的半径分别为和，圆台的侧面中存在两条母线互相垂直，则圆台侧面积的最大值为（）A.B.C.D.8.若曲线与曲线有且只有一个公共点，且在公共点处的切线相同，则实数的值为（）A.B.C.D.二、多项选择题：（本大题共4小题，每小题5分，共20分）在每小题给出的选项中有多个选项符合要求．全部选对得5分，部分选对得2分，有选错的得0分．9.已知平面向量，，则（）A.若，则B.若，则与的夹角为锐角C.若为任意非零向量，则存在实数，使得D.若在上的投影向量为，则或10.如图，透明塑料制成的长方体容器内灌进一些水，固定容器底面一边于地面上，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com再将容器以为轴顺时针旋转，则（）A.有水的部分始终是棱柱B.水面所在四边形为矩形且面积不变C.棱始终与水面平行D.当点在棱上且点在棱上（均不含端点）时，是定值11.函数的图象向右平移个单位，再将所得图象上所有点的横坐标变为原来的倍，纵坐标不变，得到函数的图象．若对于任意，都存在，使得，则的可能值为（）A.B.C.D.12.如图，已知圆锥的轴与母线所成的角为，过的平面与圆锥的轴所成的角为，该平面截这个圆锥所得的截面为椭圆，椭圆的长轴为,短轴为,长半轴长为，短半轴长为，椭圆的中心为,再以为弦且垂直于的圆截面，记该圆与直线交于，与直线交于，则下列说法正确的是（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA.当时，平面截这个圆锥所得的截面也为椭圆B.C.平面截这个圆锥所得椭圆的离心率D.平面截这个圆锥所得椭圆的离心率三、填空题（本大题共4小题，每小题5分，共20分）13.若的展开式中各项系数和为，则该二项式展开式中所有有理项的系数之和为____．14.已知点在双曲线上，且中点在直线上，线段的中垂线与轴交于点，则双曲线的离心率为____．15.若函数的定义域为，且，，则___．16.在四棱锥中，底面为正方形，，为空间中一动点，为的中点小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com平面．若，则的轨迹围成封闭图形的体积为___；若与平面所成的角等于，则平面与的轨迹的交线长为___．四、解答题（本大题共6小题，共70分）17.已知的内角对应的边分别为，的面积为．（1）求证：；（2）点在边上，若，求．18.已知为数列的前项和，，且是公差为1的等差数列．正项等比数列满足，．（1）求数列的通项；（2）求数列的前项和．19.如图，在四棱锥中，底面是等腰梯形，，，，为CD的中点，，为的重心．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（1）证明：平面；（2）求直线与平面所成角的正弦值．20.2023年3月11日，丁俊晖在泰国巴吞他尼府举行的2023斯诺克6红球世锦赛决赛中以8:6战胜泰国球员塔猜亚·乌努，第二次夺得这项赛事冠军．丁俊晖认为“中式台球更易在职业和业余之间找到平衡，更容易让台球运动在全中国乃至全世界流行起来．...