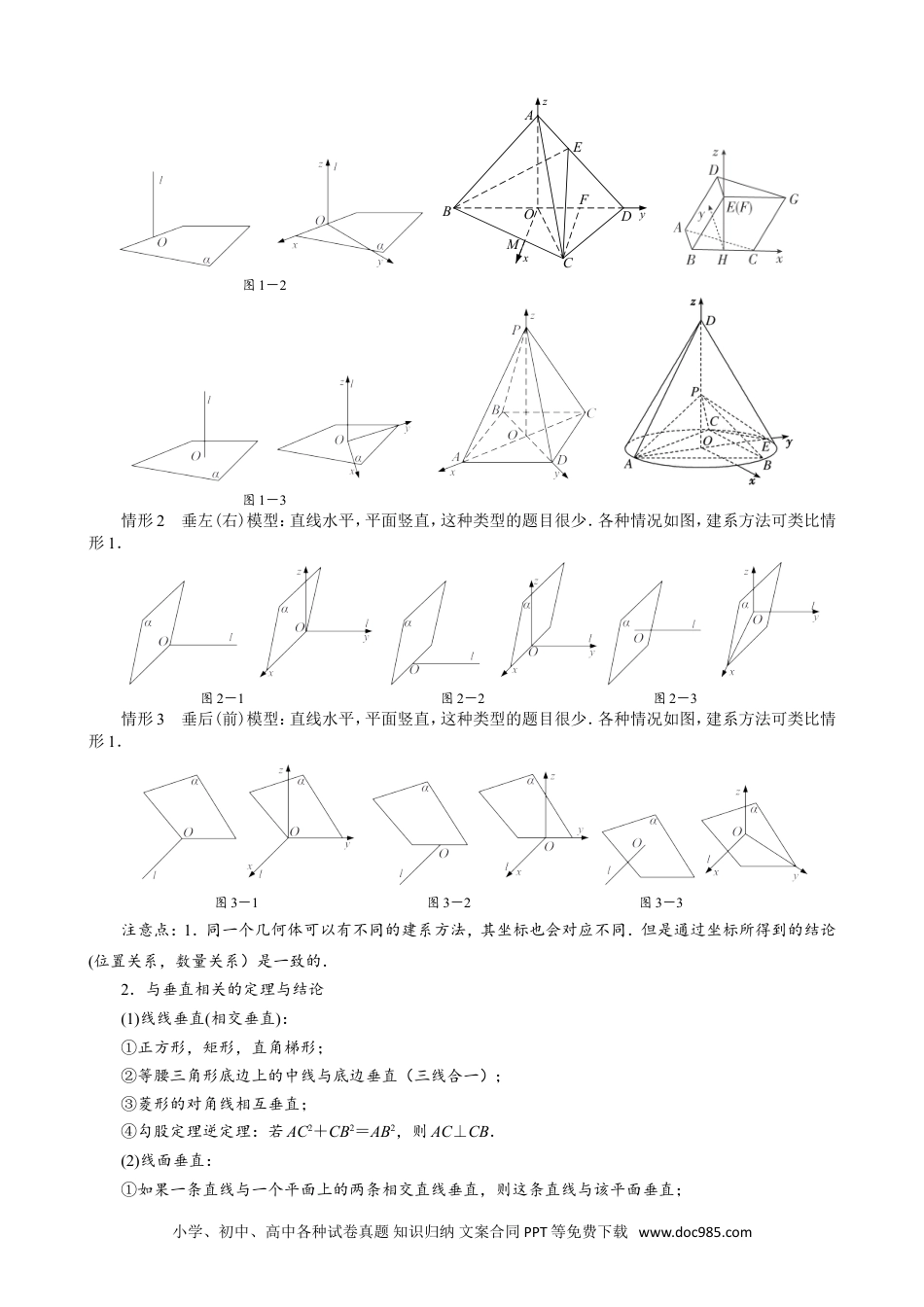
专题08立体几何中的建系求(设)点问题一、空间直角坐标系1．空间直角坐标系：在空间选定一点O和一个单位正交基底{i，j，k}，以O为原点，分别以i，j，k的方向为正方向，以它们的长为单位长度建立三条数轴：x轴、y轴、z轴，它们都叫做坐标轴，这时我们就建立了一个空间直角坐标系Oxyz．2．相关概念：O叫做原点，i，j，k都叫做坐标向量，通过每两条坐标轴的平面叫做坐标平面，分别称为Oxy平面、Oyz平面、Ozx平面，它们把空间分成八个部分．注意点：(1)基向量：|i|＝|j|＝|k|＝1，i·j＝i·k＝j·k＝0．(2)画空间直角坐标系Oxyz时，一般使∠xOy＝135°(或45°)，∠yOz＝90°．(3)建立的坐标系均为右手直角坐标系．二、空间直角坐标系的建立1．建立空间直角坐标系的原则尽可能的让更多的点位于x轴，y轴，z轴上或位于坐标平面Oxy，Oyz，Ozx内．2．空间直角坐标系建立的模型(1)墙角模型：已知条件中有过一点两两垂直的三条直线，就是墙角模型．建系：以该点为原点，分别以两两垂直的三条直线为x轴，y轴，z轴，建立空间直角坐标系Oxyz，当然条件不明显时，要先证明过一点的三条直线两两垂直(即一个线面垂直面内两条线垂直)，这个过程不能省略．然后建系．xyzOBADCA1B1C1D1EFxyzBACA1B1C1DFExyz(2)垂面模型：已知条件中有一条直线垂直于一个平面，就是墙角模型．情形１垂下(上)模型：直线竖直，平面水平，大部分题目都是这种类型．如图，此情形包括垂足在平面图形的顶点处、垂足在平面图形的边上(中点多)和垂足在平面图形的内部三种情况．第一种建系方法为以垂足为坐标原点，垂线的向上方向为z轴，平面图形的一边为x轴或y轴，在平面图形中，过原点作x轴或y轴的垂线为y轴或x轴(其中很多题目是连接垂足与平面图形的另一顶点)建立空间直角坐标系．第二种建系方法为以垂足为坐标原点，垂线的向上方向为z轴，垂足所在的一边为x轴或y轴，在平面图形中，过原点作x轴或y轴的垂线为y轴或x轴(其中很多题目是连接垂足与平面图形的另一顶点)建立空间直角坐标系．第三种建系方法为以垂足为坐标原点，垂线的向上方向为z轴，连接垂足与平面图形的一顶点所在直线为为x轴或y轴，在平面图形中，过原点作x轴或y轴的垂线为y轴或x轴(其中很多题目是连接垂足与平面图形的另一顶点)建立空间直角坐标系．图1－1小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comABCDOExyzFM图1－2图1－3情形2垂左(右)模型：直线水平，平面竖直，这种类型的题目很少．各种情况如图，建系方法可类比情形1．图2－1图2－2图2－3情形3垂后(前)模型：直线水平，平面竖直，这种类型的题目很少．各种情况如图，建系方法可类比情形1．图3－1图3－2图3－3注意点：1．同一个几何体可以有不同的建系方法，其坐标也会对应不同．但是通过坐标所得到的结论(位置关系，数量关系）是一致的．2．与垂直相关的定理与结论(1)线线垂直(相交垂直)：①正方形，矩形，直角梯形；②等腰三角形底边上的中线与底边垂直（三线合一）；③菱形的对角线相互垂直；④勾股定理逆定理：若AC2＋CB2＝AB2，则AC⊥CB．(2)线面垂直：①如果一条直线与一个平面上的两条相交直线垂直，则这条直线与该平面垂直；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com②两条平行线，如果其中一条与平面垂直，那么另外一条也与这个平面垂直；③两个平面垂直，则其中一个平面上垂直交线的直线与另一个平面垂直；④直棱柱的侧棱与底面垂直．三、空间点的坐标1．点的坐标在空间直角坐标系Oxyz中，i，j，k为坐标向量，对空间任意一点A，对应一个向量OA，且点A的位置由向量OA唯一确定，由空间向量基本定理，存在唯一的有序实数组(x，y，z)，使OA＝xi＋yj＋zk．在单位正交基底{i，j，k}下与向量OA对应的有序实数组(x，y，z)，叫做点A在空间直角坐标系中的坐标，记作A(x，y，z)，其中x叫做点A的横坐标，y叫做点A的纵坐标，z叫做点A的竖坐标．2．点的坐标的求法建系之后要能够快速准确的写出(算出)点的坐标，按照特点可以分为可直接写的点和需要计算的点下列两类．可直接写的点(1)坐标轴、坐标平面上的点的坐标点的位置x轴上y轴上z轴上Oxy平面...