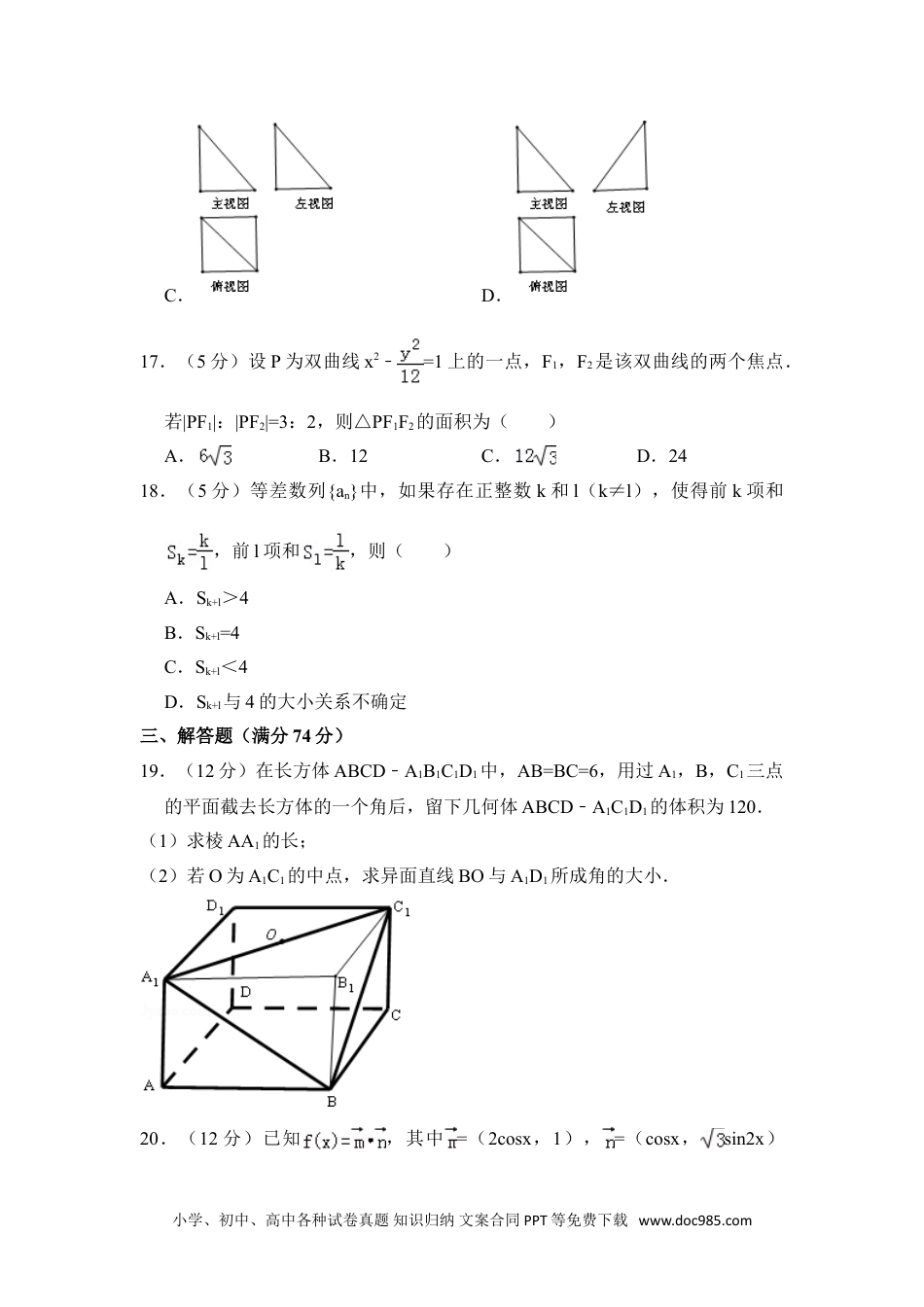
2012年上海市虹口区高考数学二模试卷（文科）一、填空题（每小题4分，满分56分）1．（4分）已知集合M={x|（x+5）（x﹣2）＜0}，N={x|1≤x≤5}，则M∩N=．2．（4分）设z=1﹣i（i为虚数单位），则=．3．（4分）若非零向量、，满足，且，则与的夹角大小为．4．（4分）已知椭圆的焦点为（0，），则实数t=．5．（4分）若等比数列{an}满足an•an+1=9n，则公比q=．6．（4分）一平面截一球得到直径为2的圆面，球心到这平面的距离为3，则该球的体积是．7．（4分）如果展开式中，第4项与第6项的系数相等，则该展开式中，常数项的值是．8．（4分）在同一平面直角坐标系中，函数y=g（x）的图象与y=3x的图象关于直线y=x对称，而函数y=f（x）的图象与y=g（x）的图象关于y轴对称，若f（a）=﹣1，则a的值是．9．（4分）在约束条件：下，目标函数z=2x﹣y的最大值为．10．（4分）执行如图所示的程序框图，若输入A的值为2，则输出P的值为．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com11．（4分）从{1，2，3，4，5，6}中随机选一个数a，从{1，2，3}中随机选一个数b，则a＜b的概率等于．12．（4分）在△ABC中，边BC=2，AB=，则角C的取值范围是．13．（4分）函数，则不等式f（x）＞﹣5的解集是．14．（4分）a，b∈R，a＞b且ab=1，则的最小值等于．二、选择题（每小题5分，满分20分）15．（5分）命题A：若函数y=f（x）是幂函数，则函数y=f（x）的图象不经过第四象限．那么命题A的逆命题、否命题、逆否命题这三个命题中假命题的个数是（）A．0B．1C．2D．316．（5分）如图是底面为正方形的四棱锥，其中棱PA垂直于底面，它的三视图正确的是（）A．B．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC．D．17．（5分）设P为双曲线x2﹣=1上的一点，F1，F2是该双曲线的两个焦点．若|PF1|：|PF2|=3：2，则△PF1F2的面积为（）A．B．12C．D．2418．（5分）等差数列{an}中，如果存在正整数k和l（k≠l），使得前k项和，前l项和，则（）A．Sk+l＞4B．Sk+l=4C．Sk+l＜4D．Sk+l与4的大小关系不确定三、解答题（满分74分）19．（12分）在长方体ABCD﹣A1B1C1D1中，AB=BC=6，用过A1，B，C1三点的平面截去长方体的一个角后，留下几何体ABCD﹣A1C1D1的体积为120．（1）求棱AA1的长；（2）若O为A1C1的中点，求异面直线BO与A1D1所成角的大小．20．（12分）已知，其中=（2cosx，1），=（cosx，sin2x）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（x∈R）．（1）求f（x）的最小正周期及单调递增区间；（2）在△ABC中，a、b、c分别是角A、B、C的对边，若f（A）=2，b=1，△ABC面积为，求：边a的长及△ABC的外接圆半径R．21．（14分）已知：函数g（x）=ax2﹣2ax+1+b（a≠0，b＜1），在区间[2，3]上有最大值4，最小值1，设函数．（1）求a、b的值及函数f（x）的解析式；（2）若不等式f（2x）﹣k•2x≥0在x∈[﹣1，1]时恒成立，求实数k的取值范围．22．（18分）已知：曲线C上任意一点到点F（1，0）的距离与到直线x=﹣1的距离相等．（1）求曲线C的方程；（2）过点F（1，0）作直线交曲线C于M，N两点，若|MN|长为，求直线MN的方程；（3）设O为坐标原点，如果直线y=k（x﹣1）交曲线C于A、B两点，是否存在实数k，使得？若存在，求出k的值；若不存在，说明理由．23．（18分）如图，平面直角坐标系中，射线y=x（x≥0）和y=0（x≥0）上分别依次有点A1、A2，…，An，…，和点B1，B2，…，Bn…，其中A1（1，1），B1（1，0），B2（2，0）．且，（n=2，3，4…）．（1）用n表示|OAn|及点An的坐标；（2）用n表示|BnBn+1|及点Bn的坐标；（3）写出四边形AnAn+1Bn+1Bn的面积关于n的表达式S（n），并求S（n）的最大值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2012年上海市虹口区高考数学二模试卷（文科）参考答案与试题解析一、填空题（每小题4分，满分56分）1．（4分）已知集合M={x|（x+5）（x﹣2）＜0}，N={x|1≤x≤5}，则M∩N={x|1≤x＜2}．【考...