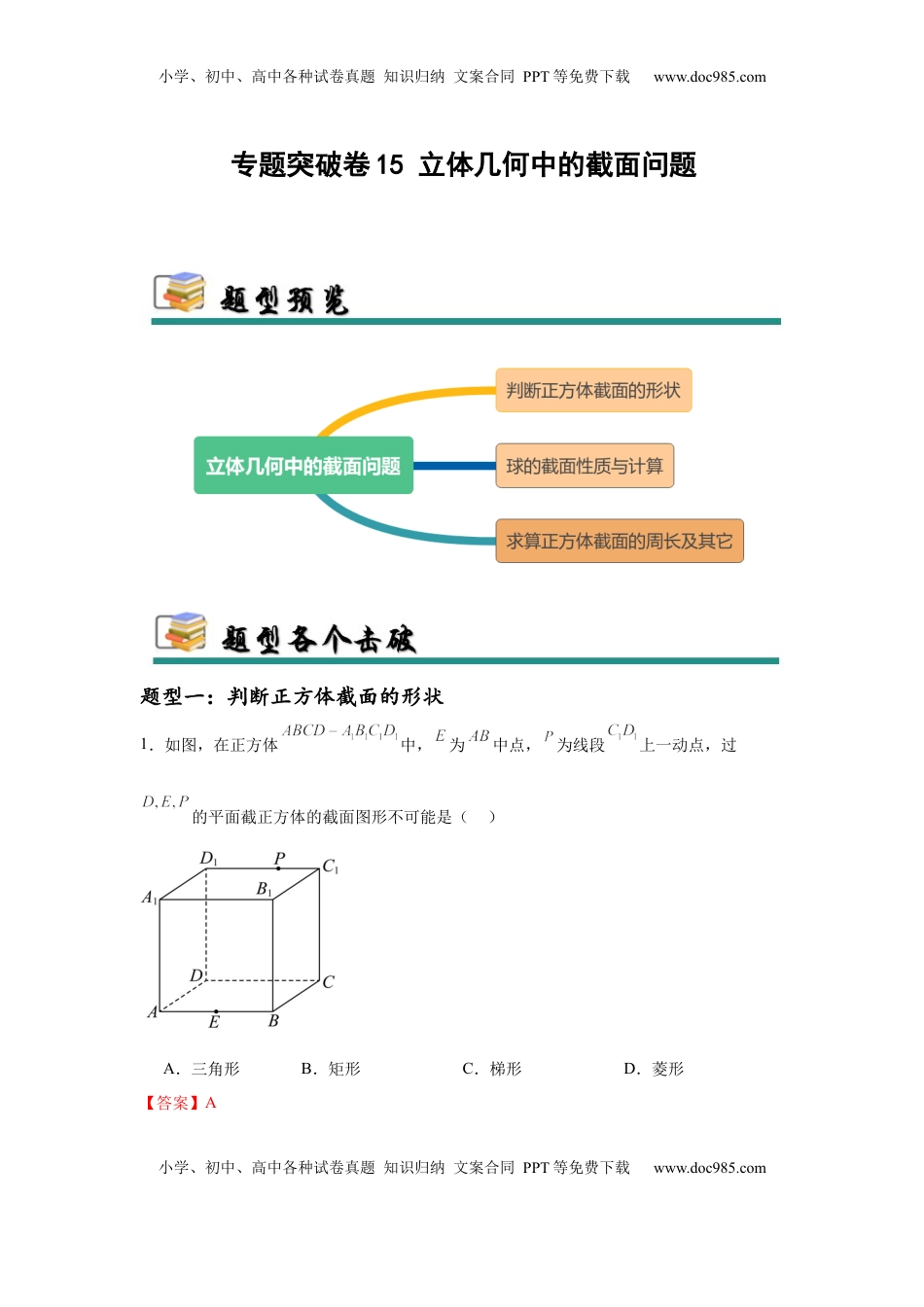
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题突破卷15立体几何中的截面问题题型一：判断正方体截面的形状1．如图，在正方体中，为中点，为线段上一动点，过的平面截正方体的截面图形不可能是（）A．三角形B．矩形C．梯形D．菱形【答案】A小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【分析】根据点在、以及三个特殊位置时，截面图形的形状，选出正确选项.【详解】B选项，当点与重合时，取中点，因为是中点，则，且，连接，则四边形为平行四边形，又因为，所以平行四边形为矩形，故排除B选项；C选项，当点与重合时，取中点，因为是的中点，所以，连接，截面四边形为梯形，故排除C选项；D选项，当点为中点时，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com因为是中点，所以且，连接，则四边形是平行四边形，又因为，，因为是正方体，所以，所以，所以平行四边形是菱形，故排除D选项；不管点在什么位置，都不可能是三角形.故选：A.2．已知正方体的棱长为2，点M、N、P分别为棱AB、、的中点，则平面MNP截正方体所得截面的面积为（）A．B．C．D．【答案】B【分析】通过平行画出截面为正六边形，然后结合正三角形面积计算其面积即可.【详解】如图所示，分别取，，的中点，，，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com连接，，，，，则，.因为，所以，同理得，.由基本事实及其三个推论得，，，，，六点共面，所以平面截正方体所得的截面是六边形.根据正方体的性质可知截面是边长为的正六边形，所求面积.故选：B3．已知正方体的棱长为6，点，分别在棱，上，且满足，点为底面的中心，过点，，作平面，则平面截正方体所得的截面面积为（）A．B．C．D．【答案】A【分析】由于上下底平行，则可得平面与上下底面的交线平行，则可得为平面与上底面的交线，为平面与下底面的交线，则梯形为小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com平面截正方体的截面，可证得梯形为等腰梯形，根据已知的数量关系求解即可.【详解】连接，，与交点即为，因为，所以‖，因为‖，所以‖，所以共面，所以平面截正方体所得的截面为梯形，因为正方体的棱长为6，且，所以，在中，，则，在中，，则，在，，则，过作于，则，所以,所以等腰梯形的面积为,故选：A小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com4．在长方体中，，点是线段上靠近的四等分点，点是线段的中点，则平面截该长方体所得的截面图形为（）A．三角形B．四边形C．五边形D．六边形【答案】C【分析】延长交的延长线于点，连接交于点，连接，延长交的延长线于点，连接交于点，连接，即可得到截面图形，再利用相似验证即可.【详解】延长交的延长线于点，连接交于点，连接，延长交的延长线于点，连接交于点，连接，则五边形为平面截该长方体所得的截面图形，不妨设，又点是线段上靠近的四等分点，点是线段的中点，所以，，，所以，又，所以，又，所以，又，即，解得，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com又，即，解得，符合题意，即五边形为平面截该长方体所得的截面图形.故选：C5．如图，在棱长为2的正方体中，内部有一个底面垂直于的圆锥，当该圆锥底面积最大时，圆锥体积最大为（）A．B．C．D．【答案】C【分析】取的中点，记为，当圆锥底面内切于正六边形时该圆锥的底面积最大，结合圆锥...