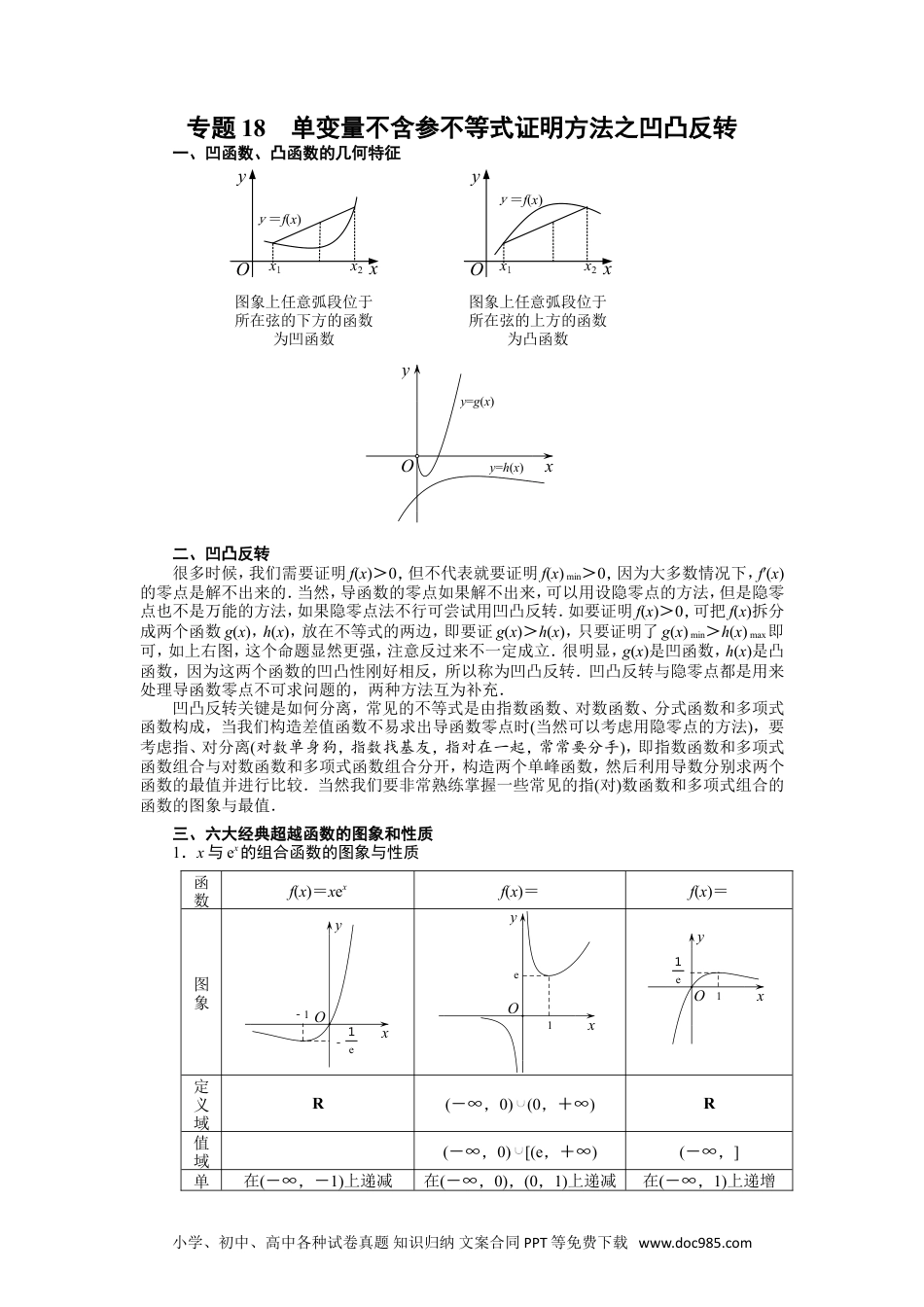
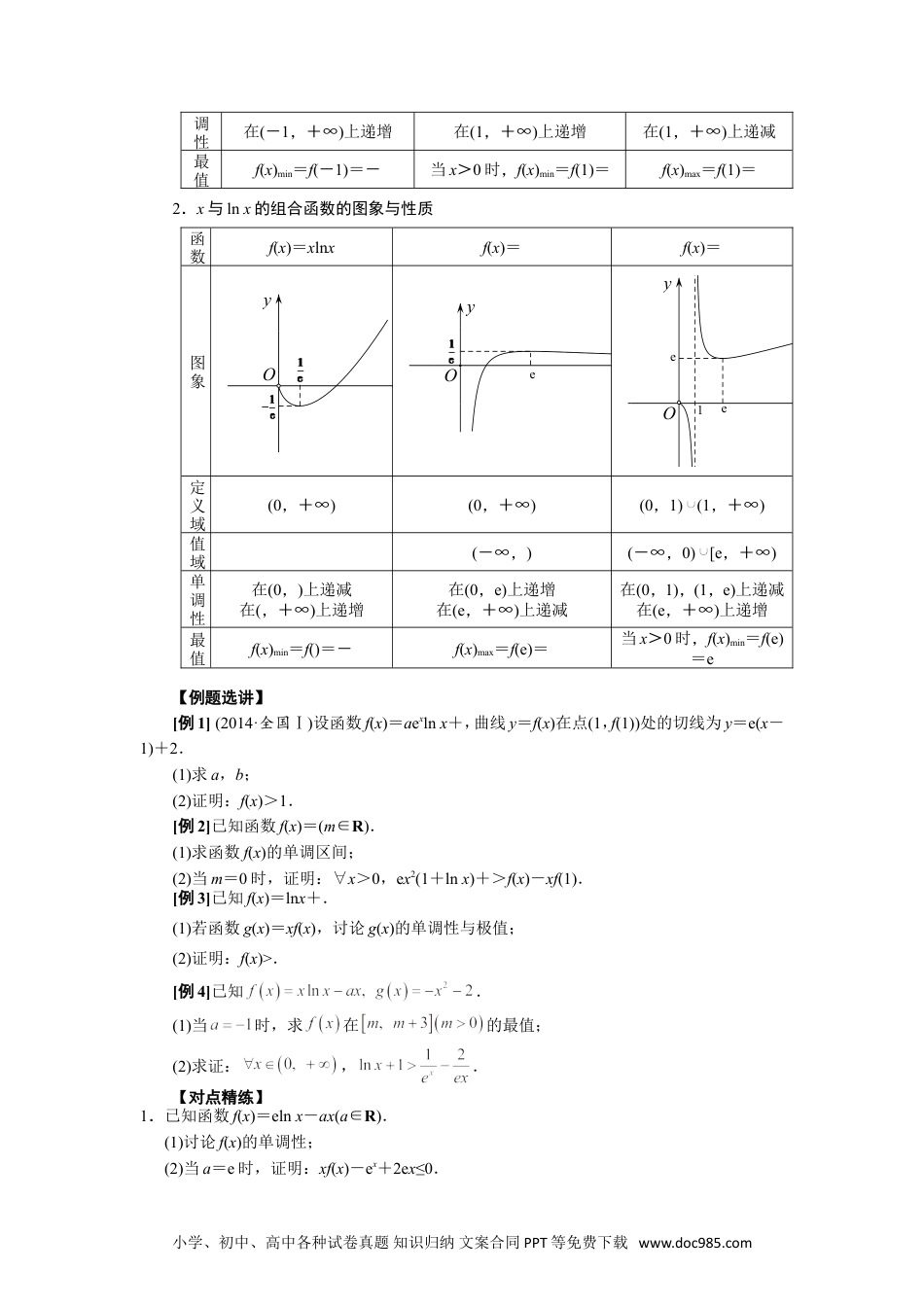
专题18单变量不含参不等式证明方法之凹凸反转一、凹函数、凸函数的几何特征xyOx1x2图象上任意弧段位于所在弦的下方的函数为凹函数y=f(x)xyOx1x2图象上任意弧段位于所在弦的上方的函数为凸函数y=f(x)xyy=h(x)y=g(x)O二、凹凸反转很多时候,我们需要证明f(x)>0,但不代表就要证明f(x)min>0,因为大多数情况下,f′(x)的零点是解不出来的.当然,导函数的零点如果解不出来,可以用设隐零点的方法,但是隐零点也不是万能的方法,如果隐零点法不行可尝试用凹凸反转.如要证明f(x)>0,可把f(x)拆分成两个函数g(x),h(x),放在不等式的两边,即要证g(x)>h(x),只要证明了g(x)min>h(x)max即可,如上右图,这个命题显然更强,注意反过来不一定成立.很明显,g(x)是凹函数,h(x)是凸函数,因为这两个函数的凹凸性刚好相反,所以称为凹凸反转.凹凸反转与隐零点都是用来处理导函数零点不可求问题的,两种方法互为补充.凹凸反转关键是如何分离,常见的不等式是由指数函数、对数函数、分式函数和多项式函数构成,当我们构造差值函数不易求出导函数零点时(当然可以考虑用隐零点的方法),要考虑指、对分离(对数单身狗,指数找基友,指对在一起,常常要分手),即指数函数和多项式函数组合与对数函数和多项式函数组合分开,构造两个单峰函数,然后利用导数分别求两个函数的最值并进行比较.当然我们要非常熟练掌握一些常见的指(对)数函数和多项式组合的函数的图象与最值.三、六大经典超越函数的图象和性质1.x与ex的组合函数的图象与性质函数f(x)=xexf(x)=f(x)=图象xy-1e-1Oxye1Oxy1e1O定义域R(-∞,0)(0,+∞)R值域(-∞,0)[(e,+∞)(-∞,]单在(-∞,-1)上递减在(-∞,0),(0,1)上递减在(-∞,1)上递增小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com调性在(-1,+∞)上递增在(1,+∞)上递增在(1,+∞)上递减最值f(x)min=f(-1)=-当x>0时,f(x)min=f(1)=f(x)max=f(1)=2.x与lnx的组合函数的图象与性质函数f(x)=xlnxf(x)=f(x)=图象yOyeOyee1O定义域(0,+∞)(0,+∞)(0,1)(1,+∞)值域(-∞,)(-∞,0)[e,+∞)单调性在(0,)上递减在(,+∞)上递增在(0,e)上递增在(e,+∞)上递减在(0,1),(1,e)上递减在(e,+∞)上递增最值f(x)min=f()=-f(x)max=f(e)=当x>0时,f(x)min=f(e)=e【例题选讲】[例1](2014·全国Ⅰ)设函数f(x)=aexlnx+,曲线y=f(x)在点(1,f(1))处的切线为y=e(x-1)+2.(1)求a,b;(2)证明:f(x)>1.[例2]已知函数f(x)=(m∈R).(1)求函数f(x)的单调区间;(2)当m=0时,证明:∀x>0,ex2(1+lnx)+>f(x)-xf(1).[例3]已知f(x)=lnx+.(1)若函数g(x)=xf(x),讨论g(x)的单调性与极值;(2)证明:f(x)>.[例4]已知.(1)当时,求在的最值;(2)求证:,.【对点精练】1.已知函数f(x)=elnx-ax(a∈R).(1)讨论f(x)的单调性;(2)当a=e时,证明:xf(x)-ex+2ex≤0.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2.已知,其中常数.(1)当时,求函数的极值;(2)求证:.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com3.设函数.(1)当时,求的极值;(2)当时,证明:在上恒成立.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com4.已知f(x)=xlnx,g(x)=-x2+ax-3.(1)若对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围.(2)证明:对一切x∈(0,+∞),lnx>-恒成立.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com5.已知函数f(x)=lnx+,g(x)=e-x+bx,a,b∈R,e为自然对数的底数.(1)若函数y=g(x)在R上存在零点,求实数b的取值范围;(2)若函数y=f(x)在x=处的切线方程为ex+y-2+b=0.求证:对任意的x∈(0,+∞),总有f(x)>g(x).小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com6.已知f(x)=xlnx.(1)求函数f(x)在[t,t+2](t>0)上的最小值;(2)证明:对一切x∈(0,+∞),都有lnx>-成立.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com