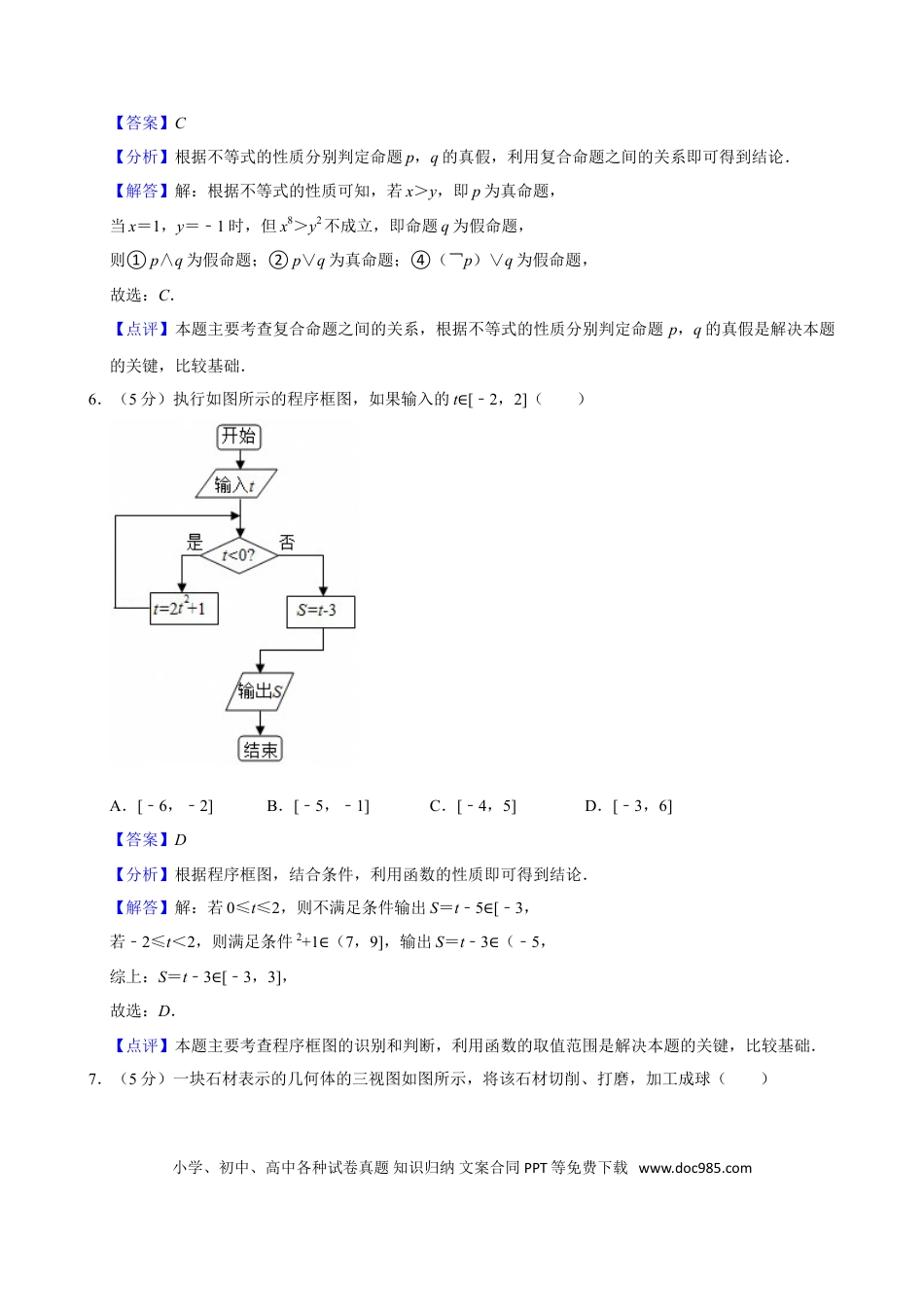
2014年湖南省高考数学试卷（理科）参考答案与试题解析一．选择题（共10小题）题号12345678910答案BDCACDBDAA一、选择题（共10小题，每小题5分，满分50分）1．（5分）满足＝i（i为虚数单位）的复数z＝（）A．+iB．﹣iC．﹣+iD．﹣﹣i【答案】B【分析】根据复数的基本运算即可得到结论．【解答】解： ＝i，∴z+i＝zi，即z＝＝＝﹣i，故选：B．【点评】本题主要考查复数的计算，比较基础．2．（5分）对一个容量为N的总体抽取容量为n的样本，当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时，总体中每个个体被抽中的概率分别为P1，P2，P3，则（）A．P1＝P2＜P3B．P2＝P3＜P1C．P1＝P3＜P2D．P1＝P2＝P3【答案】D【分析】根据简单随机抽样、系统抽样和分层抽样的定义即可得到结论．【解答】解：根据简单随机抽样、系统抽样和分层抽样的定义可知，每个个体被抽中的概率都是相等的，即P1＝P2＝P6．故选：D．【点评】本题主要考查简单随机抽样、系统抽样和分层抽样的性质，比较基础．3．（5分）已知f（x），g（x）分别是定义在R上的偶函数和奇函数，且f（x）（x）＝x3+x2+1，则f小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（1）+g（1）＝（）A．﹣3B．﹣1C．1D．3【答案】C【分析】将原代数式中的x替换成﹣x，再结合着f（x）和g（x）的奇偶性可得f（x）+g（x），再令x＝1即可．【解答】解：由f（x）﹣g（x）＝x3+x2+8，将所有x替换成﹣x，得f（﹣x）﹣g（﹣x）＝﹣x3+x2+3，根据f（x）＝f（﹣x），g（﹣x）＝﹣g（x），得f（x）+g（x）＝﹣x3+x2+3，再令x＝1，f（1）+g（1）＝1．故选：C．【点评】本题属于容易题，是对函数奇偶性的考查，在高考中，函数奇偶性的考查一般相对比较基础，学生在掌握好基础知识的前提下，做题应该没有什么障碍．本题中也可以将原代数式中的x直接令其等于﹣1也可以得到计算结果．4．（5分）（x﹣2y）5的展开式中x2y3的系数是（）A．﹣20B．﹣5C．5D．20【答案】A【分析】利用二项式定理的展开式的通项公式，求解所求项的系数即可．【解答】解：由二项式定理可知：Tr+1＝，要求解（x﹣3y）5的展开式中x2y4的系数，所以r＝3，所求系数为：＝﹣20．故选：A．【点评】本题考查二项式定理的通项公式的应用，基本知识的考查．5．（5分）已知命题p：若x＞y，则﹣x＜﹣y；命题q：若x＞y2＞y2，在命题①p∧q；②p∨q；③p∧（￢q）；④（￢p），真命题是（）A．①③B．①④C．②③D．②④小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【答案】C【分析】根据不等式的性质分别判定命题p，q的真假，利用复合命题之间的关系即可得到结论．【解答】解：根据不等式的性质可知，若x＞y，即p为真命题，当x＝1，y＝﹣1时，但x8＞y2不成立，即命题q为假命题，则①p∧q为假命题；②p∨q为真命题；④（￢p）∨q为假命题，故选：C．【点评】本题主要考查复合命题之间的关系，根据不等式的性质分别判定命题p，q的真假是解决本题的关键，比较基础．6．（5分）执行如图所示的程序框图，如果输入的t∈[﹣2，2]（）A．[﹣6，﹣2]B．[﹣5，﹣1]C．[﹣4，5]D．[﹣3，6]【答案】D【分析】根据程序框图，结合条件，利用函数的性质即可得到结论．【解答】解：若0≤t≤2，则不满足条件输出S＝t﹣5∈[﹣3，若﹣2≤t＜2，则满足条件2+1∈（7，9]，输出S＝t﹣3∈（﹣5，综上：S＝t﹣3∈[﹣3，3]，故选：D．【点评】本题主要考查程序框图的识别和判断，利用函数的取值范围是解决本题的关键，比较基础．7．（5分）一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．1B．2C．3D．4【答案】B【分析】由题意，该几何体为三棱柱，所以最大球的半径为正视图直角三角形内切圆的半径r．【解答】解：由题意，该几何体为三棱柱，则8﹣r+6﹣r＝，∴r＝2．故选：B．【点评】本题考查三视图，考查几何体的内切圆，考查学生的计算能力，属于基础题．8．（5分）某市生产总值连续两年持续增加，第一年的增长率为p，第二年的增长率为q（...