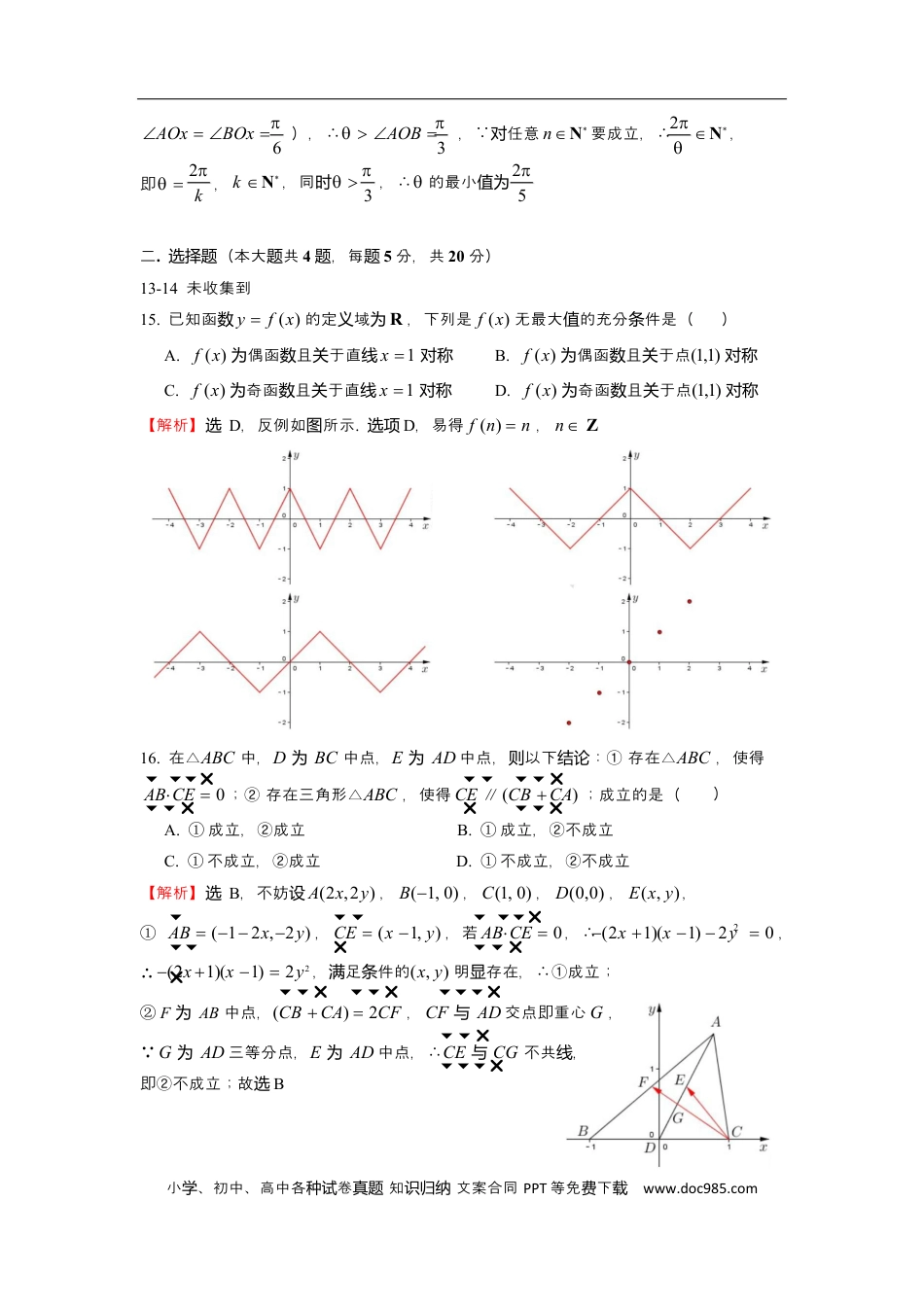
小、初中、高中各卷知文案合同学种试真题识归纳PPT等免下费载www.doc985.com2021年上海市春季高考卷数学试2021.01一.空（本大共填题题12，分题满54分，第1~6每题题4分，第7~12每题题5分）1-8未收集到9.在无等比列穷数{a}中，lim(aa)4，则a的取范是值围n1n2n【解析】(4,0)(0,4)，由意，题q(1,0)(0,1)，∴lima0，nn∴lim(aa)a4，∴aaq4q(4,0)(0,4)1n121n10.某人某天需要大于等于运动总时长60分，有五可以，如下表所示，钟现项运动选择问有几方式合种运动组A运动B运动8点9点9点10点10点11点11点12点20分钟40分钟30分钟30分钟C运动D运动E运动7点8点30分钟【解析】23，由意，至少要题选2，且种运动并选2的情中，种运动况AB、DB、EB的组合是不符意的，∴题C5C5C5C53235432y211.已知椭圆x21（0b1）的左、右焦点为F、F，以O点，为顶F焦点作为2122b抛物交于线椭圆P，且PFF45，抛物的准方程是则线线12【解析】x12，设F(c,0)，F(c,0)，抛物则线y24cx，直线PF1:yxc，124cx2y立联yxc，∴P(c,2c)，∴PFFF，PFFF2c，PF22c，2122121∴PFPF(222)c2a2c21，即准方程线为xc1212312.已知0，任意对nN*，存在总实数，使得cos(n)，则的最小是值22【解析】，在位中分析，由意，单圆题n的要落在中影部分域（其中终边图阴区5小、初中、高中各卷知文案合同学种试真题识归纳PPT等免下费载www.doc985.com2AOxBOx），∴AOB， 任意对nN*要成立，∴N*，632即，2kN*，同时，∴的最小值为k35二.（本大共选择题题4，每题题5分，共20分）13-14未收集到15.已知函数yf(x)的定域义为R，下列是f(x)无最大的充分件是（值条）A.f(x)偶函且于直为数关线x1对称C.f(x)奇函且于直为数关线x1对称B.f(x)偶函且于点为数关(1,1)对称D.f(x)奇函且于点为数关(1,1)对称【解析】选D，反例如所示图.选项D，易得f(n)n，nZ16.在△ABC中，D为BC中点，E为AD中点，以下：①则结论存在△ABC，使得ABCE0；②存在三角形△ABC，使得CE∥(CBCA)；成立的是（）A.①成立，②成立B.①成立，②不成立C.①不成立，②成立D.①不成立，②不成立【解析】选B，不妨设A(2x,2y)，B(1,0)，C(1,0)，D(0,0)，E(x,y)，①AB(12x,2y)，CE(x1,y)，若ABCE0，∴(2x1)(x1)2y0，2∴(2x1)(x1)2y2，足件的满条(x,y)明存在，∴①成立；显②F为AB中点，(CBCA)2CF，CF与AD交点即重心G， G为AD三等分点，E为AD中点，∴CE与CG不共，线即②不成立；故选B小、初中、高中各卷知文案合同学种试真题识归纳PPT等免下费载www.doc985.com三.解答（本大共题题5，共题14+14+14+16+18=76分）17.四棱锥PABCD，底面正方形为ABCD，边长为4，E为AB中点，PE平面ABCD.（1）若△PAB等三角形，求四为边棱锥PABCD的体；积（2）若CD的中点为F，PF平面与ABCD所成角为45°，求PD与AC所成角的大小.【解析】（1） 正方形ABCD边长为4，△PAB等三角形，为边E为AB中点，∴PE23，13233VPABCD4223；3（2）如建系，图P(0,0,4)，D(2,4,0)，A(2,0,0)，C(2,4,0)，∴PD(2,4,4)，AC(4,4,0)，PDAC82∴cos，|PD||AC|64262即PD与AC所成角的大小为arccos61418.已知A、B、C△为ABC的三角，个内a、b、c是其三，条边a2，cosC（1）若sinA2sinB，求b、c；.4（2）cos(A)，求c.452212c21【解析】（1）sinA2sinBa2b，∴b1，cosCc6；22144721021154（2）cos(A)cosA，∴sinA， cosCsinC，451042c530由正弦定理，csinAsinC2小、初中、高中各卷知文案合同学种试真题识归纳PPT等免下费载www.doc985.com19.（1）在团队O点西、侧东侧20千米有处设A、B站点，量距离一点两测发现P足满|PA|...