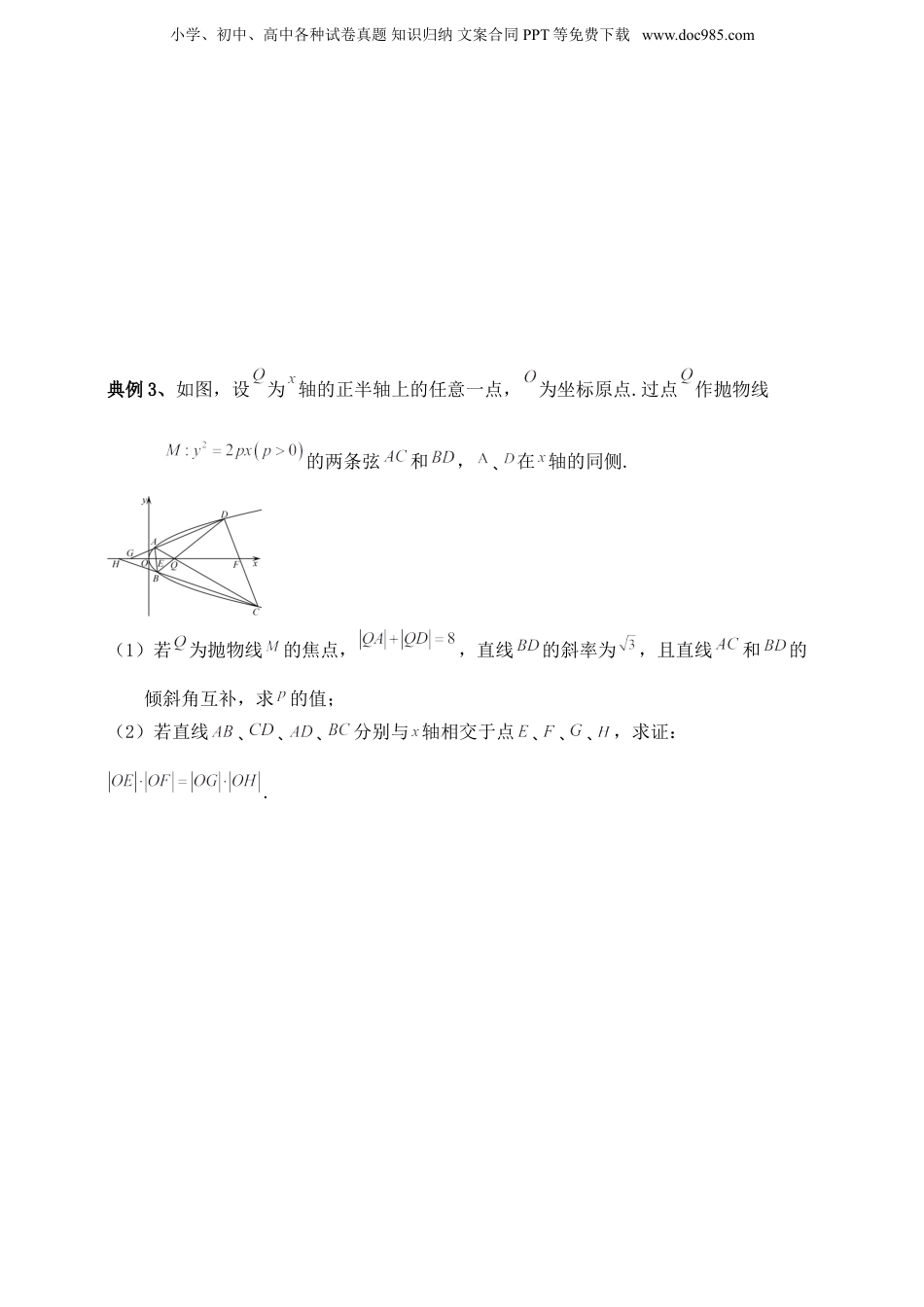
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com人教A版数学--高考解析几何复习专题七知识点一求抛物线的切线方程,由中点弦坐标或中点弦方程、斜率求参数,根据焦点或准线写出抛物线的标准方程典例1、已知抛物线的焦点为，为坐标原点．（1）过作垂直于轴的直线与抛物线交于两点，的面积为．求抛物线的标准方程；（2）抛物线上有两点，若为正三角形，求的边长．随堂练习：已知抛物线的焦点为，为抛物线上的动点，为在动直线上的投影，当为等边三角形时，其面积为.（1）求抛物线的方程；（2）设为原点，过点的直线与相切，且与椭圆交于A，两点，直线与线段交于点，试问：是否存在，使得和的面积相等恒成立？若存在，求的值；若不存在，请说明理由.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com典例2、已知P为抛物线E：上任意一点，过点P作轴，垂足为O，点在抛物线上方（如图所示），且的最小值为9．（1）求E的方程；（2）若直线与抛物线E相交于不同的两点A，B，线段AB的垂直平分线交x轴于点N，且为等边三角形，求m的值．随堂练习：已知抛物线C：上的点到其焦点F的距离为2．（1）求抛物线C的方程；（2）已知点D在直线l：上，过点D作抛物线C的两条切线，切点分别为A，B，直线AB与直线l交于点M，过抛物线C的焦点F作直线AB的垂线交直线l于点N，当|MN|最小时，求的值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com典例3、如图，设为轴的正半轴上的任意一点，为坐标原点.过点作抛物线的两条弦和，､在轴的同侧.（1）若为抛物线的焦点，，直线的斜率为，且直线和的倾斜角互补，求的值；（2）若直线､､､分别与轴相交于点､､､，求证：.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com随堂练习：已知抛物线，点为其焦点，为上的动点，为在动直线上的投影.当为等边三角形时，其面积为.（1）求抛物线的方程；（2）过轴上一动点作互相垂直的两条直线，与抛物线分别相交于点A，B和C，D，点H，K分别为，的中点，求面积的最小值.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com知识点二抛物线中的三角形或四边形面积问题,直线与抛物线交点相关问题典例4、已知曲线M上的任意一点到点的距离比它到直线的距离小1．（1）求曲线M的方程；（2）设点．若过点的直线与曲线M交于B，C两点，求的面积的最小值．随堂练习：如图，已知直线与抛物线交于A，B两点，且OA⊥OB，OD⊥AB，交AB于点D，点D的坐标为(4,2).小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（1）求p的值；（2）求△AOB的面积.典例5、已知抛物线，为坐标原点，过焦点的直线与抛物线交于不同两点.（1）记和的面积分别为，若，求直线的方程；（2）判断在轴上是否存在点，使得四边形为矩形，并说明理由.随堂练习：已知抛物线的焦点为，准线为.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（1）设与轴的交点为，点在上，且在轴上方，若，求直线的方程；（2）过焦点的直线与相交于、两点，点在上，且，，求的面积.典例6、如图，已知抛物线，直线l过点与抛物线交于A、B两点，且在A、B处的切线交于点P，过点P且垂直于x轴的直线分别交抛物线C、直线l于M、N两点．直线l与曲线交于C、D两点．（1）求证：点N是中点；（2）设的面积分别为，求的取值范围．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com随堂练习：如图，点是轴左侧（不含轴）一点，抛物线上存在不同的两点，且的中点均在抛物线C上.1、若，点A在第一象限，求此时点A的坐标；2、设中点为，求证：直线轴；3、若是曲线上的动点，求面积的最大值.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【正确答案】1、；2、证明见解析；3、人教A版数学--高考解析几何复习专题七答案典例1、答案：（1）（2）解：（1）由抛物线方程知：，为抛物线的通径，则，，解得：，抛物线的标准方程为：.小学、初中、高中各种试卷真题知识归纳文案合同PPT...