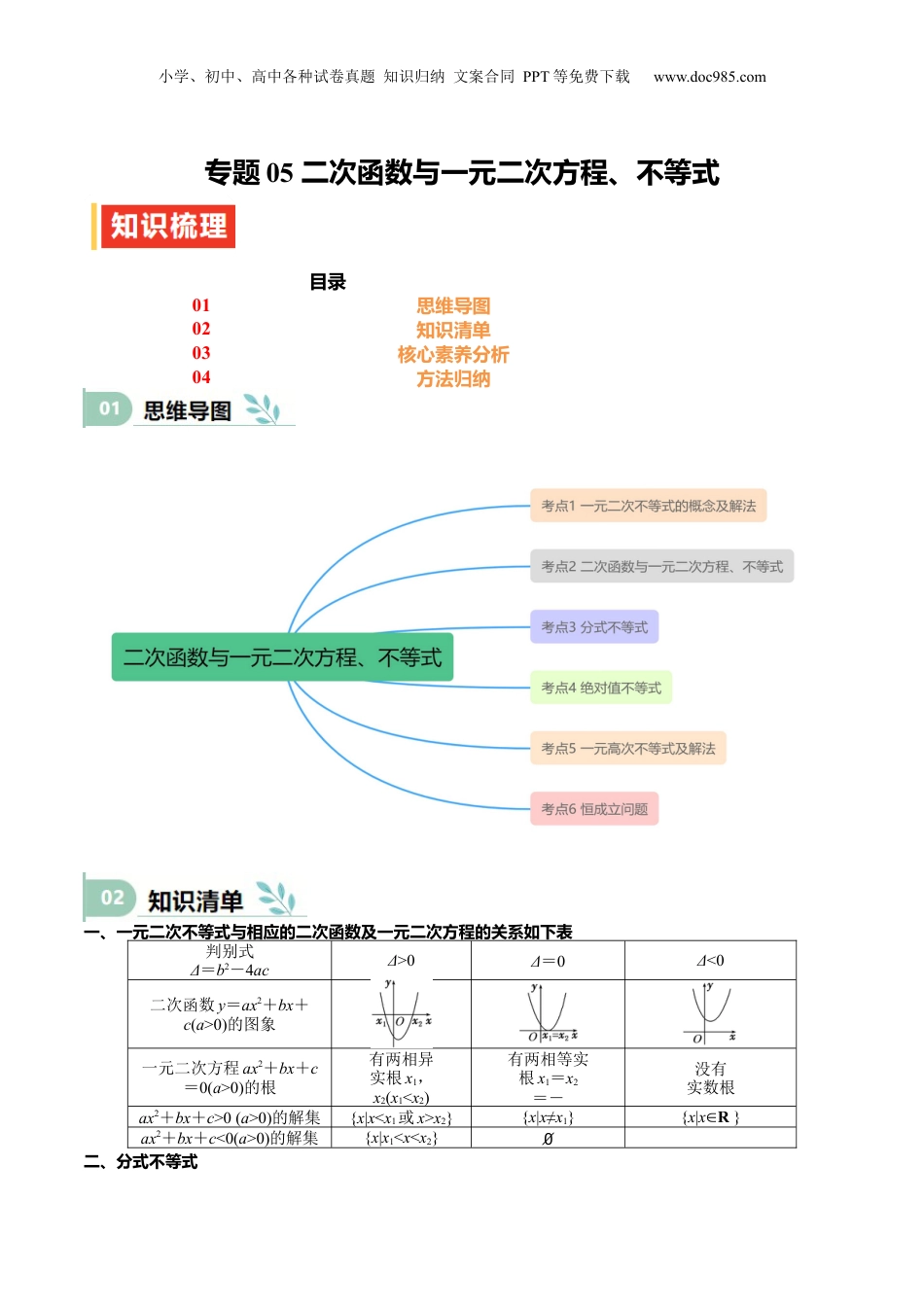
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题05二次函数与一元二次方程、不等式目录01思维导图02知识清单03核心素养分析04方法归纳一、一元二次不等式与相应的二次函数及一元二次方程的关系如下表判别式Δ＝b2－4acΔ>0Δ＝0Δ<0二次函数y＝ax2＋bx＋c(a>0)的图象一元二次方程ax2＋bx＋c＝0(a>0)的根有两相异实根x1，x2(x1<x2)有两相等实根x1＝x2＝－没有实数根ax2＋bx＋c>0(a>0)的解集{x|x<x1或x>x2}{x|x≠x1}{x|x∈R}ax2＋bx＋c<0(a>0)的解集{x|x1<x<x2}∅二、分式不等式小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（1）（2）（3）（4）三、绝对值不等式（1）（2）；；（3）含有两个或两个以上绝对值符号的不等式，可用零点分段法和图象法求解四、一元高次不等式及其解法1、概念只含有一个未知数，最高次项的次数高于二次的不等式称为高次不等式.2、一元高次不等式的解法一元高次不等式的常用解法是数轴标根法，又称穿针引线法，其具体步骤为1.化形：将不等式的一侧化为一次因式或二次不可约因式的积，且每个因式最高次项的系数为正，另一侧化为0;2.求根，标根；求出各因式所对应的方程的根，在数轴上依次标出温馨提示:要仔细区分点的虚实.3.画曲线；数轴的最右端上方起，从右到左依次经过各个根画曲线；温馨提示:奇次重根穿过数轴，偶次重根穿而不过.4.写解集：在数轴上画出曲线后，根据不等号的方向，写出不等式的解集.温馨提示:1.考虑端点是否能取到；2.各因式中最高次项系数必须为正.例：不等式的解集是_____________答案：用函数理解方程和不等式是数学的基本思想方法。本专题的学习，可以帮助学生用一元二次函数认识一元二次方程和一元二次不等式。通过梳理初中数学的相关内容，理解函数、方程和不等式之间的联系，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com体会数学的整体性。一、不含参数的一元二次不等式的解法解一元二次不等式的四个步骤命题点1不含参的不等式例1(1)不等式－2x2＋x＋3<0的解集为()A.B.C.D.答案C解析－2x2＋x＋3<0可化为2x2－x－3>0，即(x＋1)(2x－3)>0，∴x<－1或x>.(2)(多选)已知集合M＝，集合N＝，则()A．M＝B．N＝C．M∪N＝D．M∩N＝答案ACD解析由题设可得M＝[－1,3]，N＝(－1,4]，故A正确，B错误；M∪N＝{x|－1≤x≤4}，故C正确；而M∩N＝{x|－1<x≤3}，故D正确．二、含参数的一元二次不等式的解法小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com命题点2含参的不等式例2解关于x的不等式ax2－(a＋1)x＋1<0(a>0)．解原不等式变为(ax－1)(x－1)<0，因为a>0，所以(x－1)<0.所以当a>1时，解得<x<1；当a＝1时，解集为；∅当0<a<1时，解得1<x<.综上，当0<a<1时，不等式的解集为；当a＝1时，不等式的解集为；∅当a>1时，不等式的解集为.延伸探究在本例中，把a>0改成a∈R，解不等式．解当a>0时，同例2，当a＝0时，原不等式等价于－x＋1<0，即x>1，当a<0时，<1，原不等式可化为(x－1)>0，解得x>1或x<.综上，当0<a<1时，不等式的解集为，当a＝1时，不等式的解集为，∅当a>1时，不等式的解集为，当a＝0时，不等式的解集为{x|x>1}，当a<0时，不等式的解集为.拓展解关于x的不等式x2－ax＋1≤0.解由题意知，Δ＝a2－4，当①a2－4>0，即a>2或a<－2时，方程x2－ax＋1＝0的两根为x＝，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com原不等式的解为≤∴x≤.若②Δ＝a2－4＝0，则a＝±2.当a＝2时，原不等式可化为x2－2x＋1≤0，即(x－1)2≤0，∴x＝1；当a＝－2时，原不等式可化为x2＋2x＋1≤0，即(x＋1)2≤0，∴x＝－1.当③Δ＝a2－4<0，即－2<a<2时，原不等式的解集为∅.综上，当a>2或a<－2时，原不等式的解集为；当a＝2时，原不等式的解集为{1}；当a＝－2时，原不等式的解集为{－1}；当－2<a<2时，原不等式的解集为∅.三、一元二次不等式恒(能)成立问题1.一元二次不等式恒成立的条件(1)ax2＋bx＋c>0(a≠0)恒成立的充要条件是(2)ax2＋bx＋c<0(a≠0)恒成立的充要条件是2.一元二次不等式在给定区间上的恒成立问...