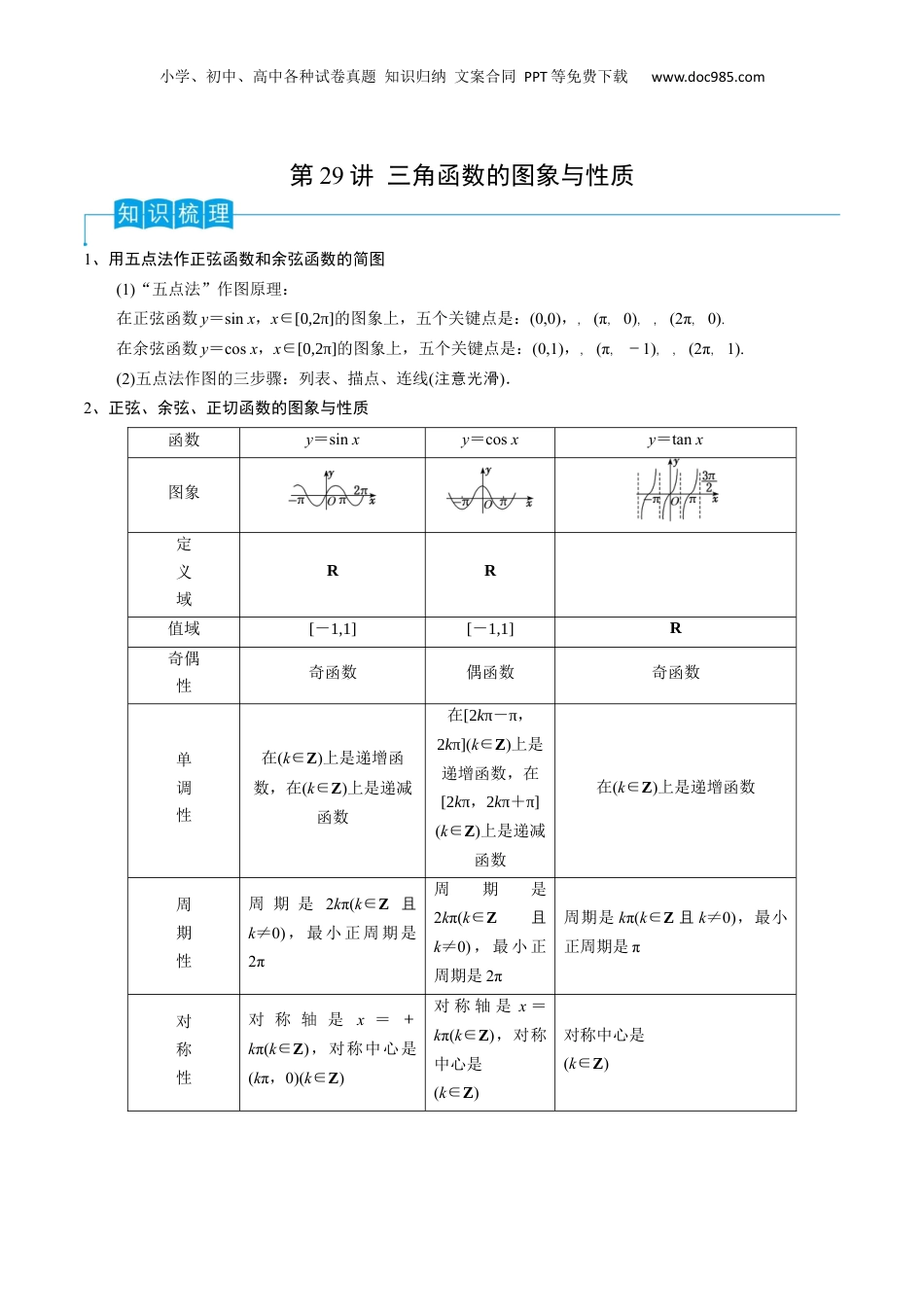
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第29讲三角函数的图象与性质1、用五点法作正弦函数和余弦函数的简图(1)“五点法”作图原理：在正弦函数y＝sinx，x∈[0,2π]的图象上，五个关键点是：(0,0)，，(π，0)，，(2π，0)．在余弦函数y＝cosx，x∈[0,2π]的图象上，五个关键点是：(0,1)，，(π，－1)，，(2π，1).(2)五点法作图的三步骤：列表、描点、连线(注意光滑)．2、正弦、余弦、正切函数的图象与性质函数y＝sinxy＝cosxy＝tanx图象定义域RR值域[－1,1][－1,1]R奇偶性奇函数偶函数奇函数单调性在(k∈Z)上是递增函数，在(k∈Z)上是递减函数在[2kπ－π，2kπ](k∈Z)上是递增函数，在[2kπ，2kπ＋π](k∈Z)上是递减函数在(k∈Z)上是递增函数周期性周期是2kπ(k∈Z且k≠0)，最小正周期是2π周期是2kπ(k∈Z且k≠0)，最小正周期是2π周期是kπ(k∈Z且k≠0)，最小正周期是π对称性对称轴是x＝＋kπ(k∈Z)，对称中心是(kπ，0)(k∈Z)对称轴是x＝kπ(k∈Z)，对称中心是(k∈Z)对称中心是(k∈Z)小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1、（2023年全国1卷）已知函数在区间有且仅有3个零点，则的取值范围是________．【命题意图】本题考查三角函数图象和零点问题，考查数学运算的核心素养.难度：中等偏下.【答案】【分析】令，得有3个根，从而结合余弦函数的图象性质即可得解.【详解】因为，所以，令，则有3个根，令，则有3个根，其中，结合余弦函数的图象性质可得，故，故答案为：.2、【2022年北京】已知函数f(x)=cos2x−sin2x，则（）A．f(x)在(−π2,−π6)上单调递减B．f(x)在(−π4,π12)上单调递增C．f(x)在(0,π3)上单调递减D．f(x)在(π4,7π12)上单调递增【答案】C【解析】【分析】化简得出f(x)=cos2x，利用余弦型函数的单调性逐项判断可得出合适的选项.【详解】因为f(x)=cos2x−sin2x=cos2x.对于A选项，当−π2<x<−π6时，−π<2x<−π3，则f(x)在(−π2,−π6)上单调递增，A错；对于B选项，当−π4<x<π12时，−π2<2x<π6，则f(x)在(−π4,π12)上不单调，B错；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com对于C选项，当0<x<π3时，0<2x<2π3，则f(x)在(0,π3)上单调递减，C对；对于D选项，当π4<x<7π12时，π2<2x<7π6，则f(x)在(π4,7π12)上不单调，D错.故选：C.1、y＝|cosx|的一个单调递增区间是()A.B．[0，π]C.D.【答案】D【解析】将y＝cosx的象位于图x下方的部分于轴关x向上翻折，轴对称x上方轴(或x上轴)的象不图变，即得y＝|cosx|的象图(如图)．故选D.2、函数f(x)＝的定域义为()A.(k∈Z)B.(k∈Z)C.(k∈Z)D.(k∈Z)【答案】B【解析】由意，得题2sinx－1≥0，x∈(k∈Z)，则x∈(k∈Z)．3、（2022·河北邯郸·二模）函数在上的值域为（）A．B．C．D．【答案】C【解析】当时，，当时，即时，取最大值小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1，当，即时，取最小值大于，故值域为故选：C4、（2022·湖北·荆州中学模拟预测）已知函数在单调递减，则的最大值为（）A．B．C．D．【答案】B【解析】，令，解得，，因为，所以，则，故，解得，所以最大值为．故选：B．5、（多）选（2022·常一模）苏锡镇下列函数中，最大值是1的函数有()A.y＝|sinx|＋|cosx|B.y＝sin2x－cos2xC.y＝4sin2xcos2xD.y＝【答案】BC.【解析】于对A，y＝＝≤，且当仅当sin2x＝±1，即x＝＋，k∈Z取时“＝”，即当x＝＋，k∈Z，时ymax＝，故A；于错误对B，y＝－(cos2x－sin2x)＝－cos2x≤1，且当仅当2x＝2kπ－π，即x＝kπ－，k∈Z时取“＝”，即当x＝kπ－，k∈Z，时ymax＝1，故B正确；于对C，y＝(2sinxcosx)2＝sin22x≤1，且当仅当sin2x＝±1，即x＝＋，k∈Z取时“＝”，即当x＝＋，k∈Z，时ymax＝1，故C正确；于对D，依意，由题tanx，tan2x都有意，且义tan2x－tanx≠0，得x≠kπ，且x≠kπ＋，且x≠＋，k∈Z，y＝＝＝＝sin2x，显然sin2x最大值为1，此，时x＝kπ＋，k∈Z，而kπ＋，k∈Z使函数y＝无意，即义sin2x不能取到1，故D不正确．故选BC.小学、初中、高...