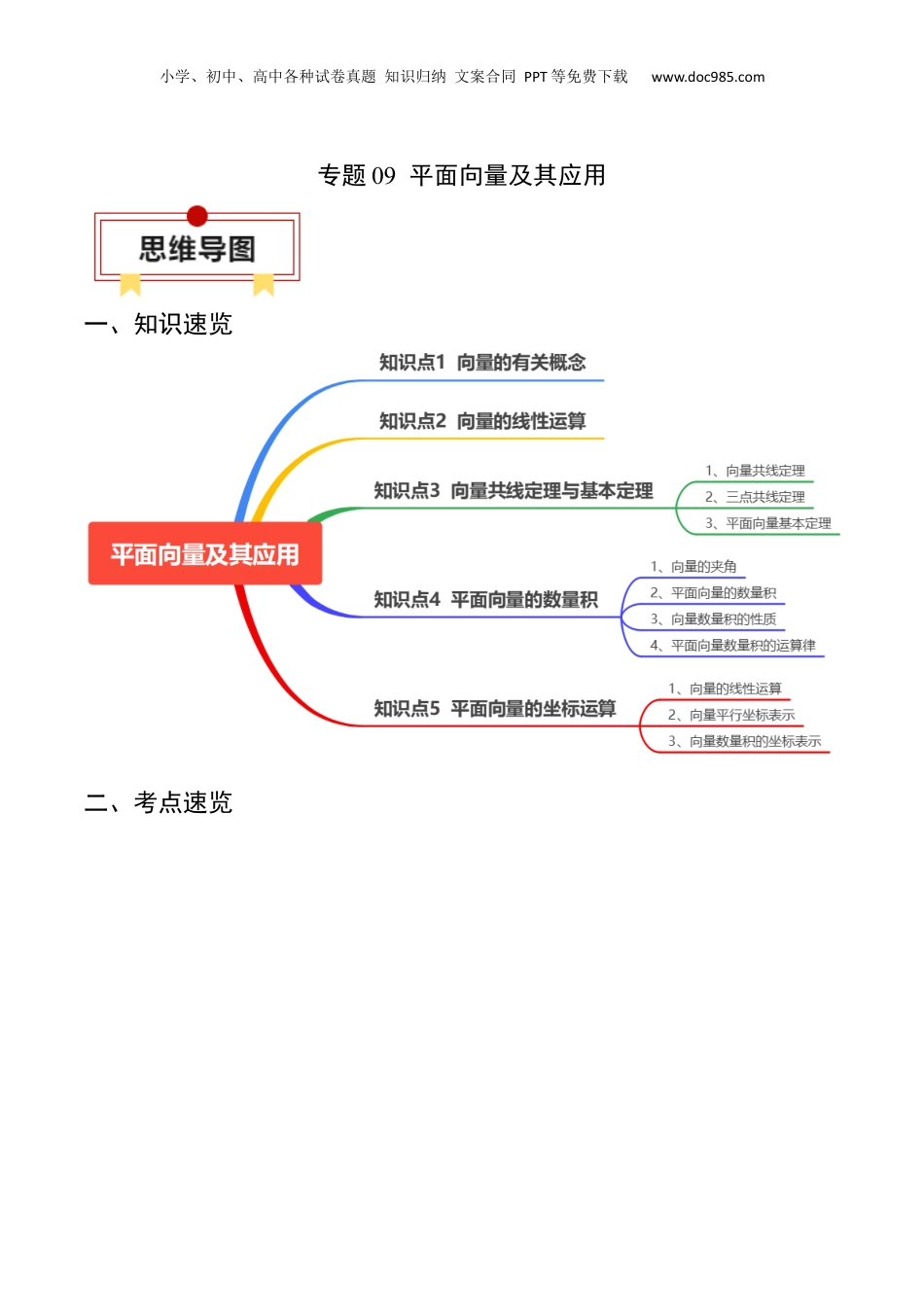
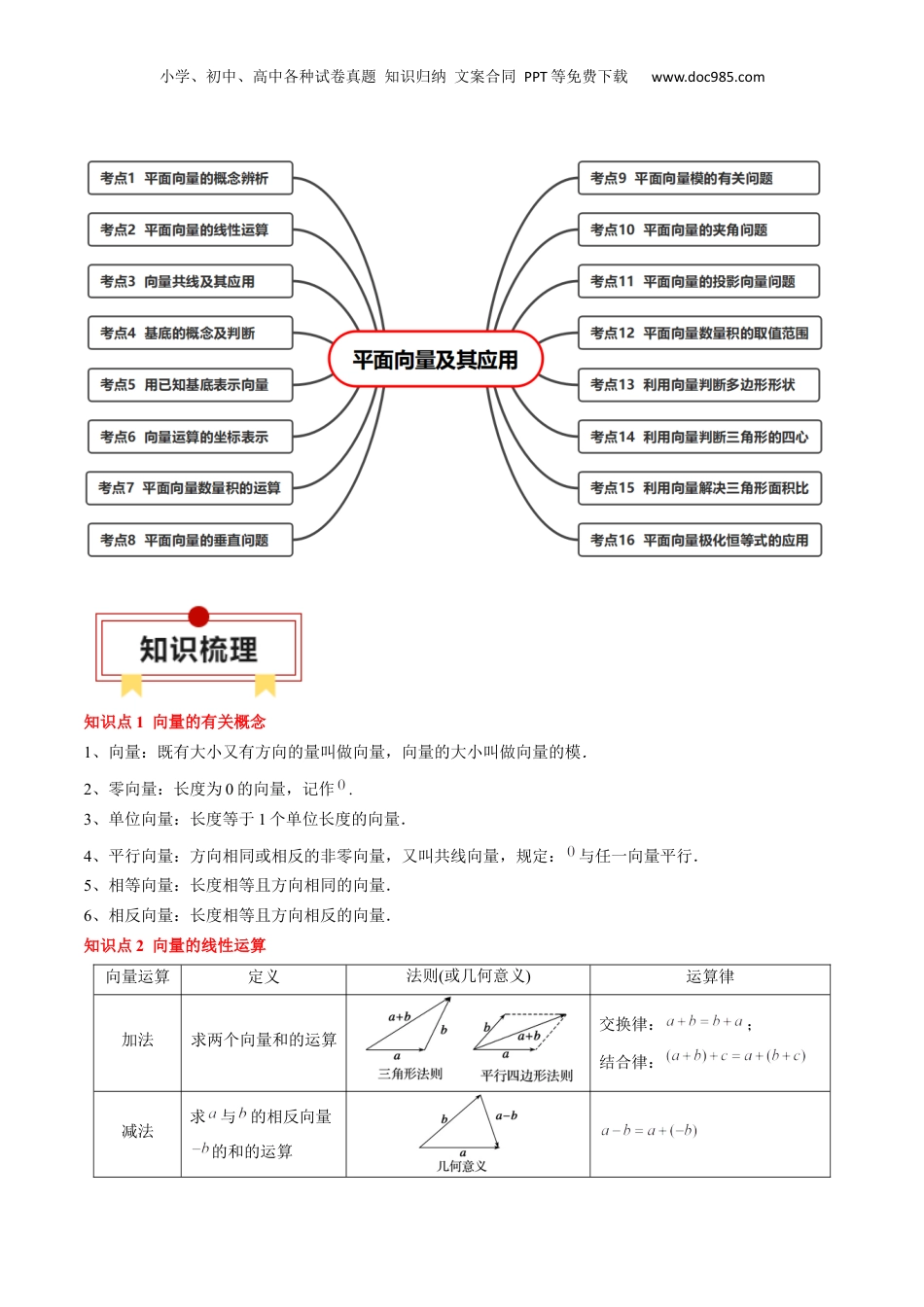
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题09平面向量及其应用一、知识速览二、考点速览小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com知识点1向量的有关概念1、向量:既有大小又有方向的量叫做向量,向量的大小叫做向量的模.2、零向量:长度为0的向量,记作.3、单位向量:长度等于1个单位长度的向量.4、平行向量:方向相同或相反的非零向量,又叫共线向量,规定:与任一向量平行.5、相等向量:长度相等且方向相同的向量.6、相反向量:长度相等且方向相反的向量.知识点2向量的线性运算向量运算定义法则(或几何意义)运算律加法求两个向量和的运算交换律:;结合律:减法求与的相反向量的和的运算小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com数乘求实数λ与向量的积的运算,当λ>0时,与的方向相同;当λ<0时,与的方向相反;当λ=0时,;;知识点3向量共线定理与基本定理1、向量共线定理:如果,则,反之,如果且,则一定存在唯一的实数,使.2、三点共线定理:平面内三点、、三点共线的充要条件是:存在实数,使,其中,为平面内一点。3、平面向量基本定理(1)定义:如果是同一平面内的两个不共线向量,那么对于这一平面内的任一向量,有且只有一对实数,使(2)基底:若不共线,我们把叫做表示这一平面内所有向量的一个基底.(3)对平面向量基本定理的理解①基底不唯一,只要是同一平面内的两个不共线向量都可以作为基底.同一非零向量在不同基底下的分解式是不同的.②基底给定时,分解形式唯一.是被唯一确定的数值.③是同一平面内所有向量的一组基底,则当与共线时,;当与共线时,;当时,.④由于零向量与任何向量都是共线的,因此零向量不能作为基底中的向量.知识点4平面向量的数量积1、向量的夹角(1)定义:已知两个非零向量和,作,,则∠AOB就是向量与的夹角.(2)范围:设θ是向量与的夹角,则0°≤θ≤180°.(3)共线与垂直:若θ=0°,则与同向;若θ=180°,则与反向;若θ=90°,则与垂直.2、平面向量的数量积小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)定义:已知两个非零向量与,它们的夹角为θ,则数量叫做与的数量积(或内积),记作,即,规定零向量与任一向量的数量积为0,即.(2)几何意义:数量积等于的长度与在的方向上的投影的乘积.【注意】(1)数量积也等于的长度|b|与在方向上的投影的乘积,这两个投影是不同的.(2)在方向上的投影也可以写成,投影是一个数量,可正可负可为0,取决于θ角的范围.3、向量数量积的性质设,是两个非零向量,是单位向量,α是与的夹角,于是我们就有下列数量积的性质:(1).(2).(3),同向⇔;,反向⇔.特别地或.(4)若θ为,的夹角,则.4、平面向量数量积的运算律(1)(交换律).(2)(结合律).(3)(分配律).【注意】对于实数a,b,c有,但对于向量,,而言,不一定成立,即不满足向量结合律.这是因为表示一个与c共线的向量,而表示一个与a共线的向量,而与不一定共线,所以不一定成立.知识点5平面向量的坐标运算1、向量的线性运算坐标表示(1)已知,则,.结论:两个向量和与差的坐标分别等于这两个向量相应坐标的和与差.(2)若,则()axy=,;小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com结论:实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标。2、向量平行坐标表示:已知,则向量,共线的充要条件是3、向量数量积的坐标表示已知非零向量,,与的夹角为θ.结论几何表示坐标表示模夹角的充要条件与的关系一、解决向量概念问题的关键点1、相等向量具有传递性,非零向量的平行也具有传递性.2、共线向量即平行向量,它们均与起点无关.3、相等向量不仅模相等,而且方向也相同,所以相等向量一定是平行向量,但平行向量未必是相等向量.4、向量可以平移,平移后的向量与原向量是相等向量.解题时,不要把它与函数图象的平移混为一谈.5、非零向量与的关系:是方向上的单位向量,因此单位向量与方向相同.6、...