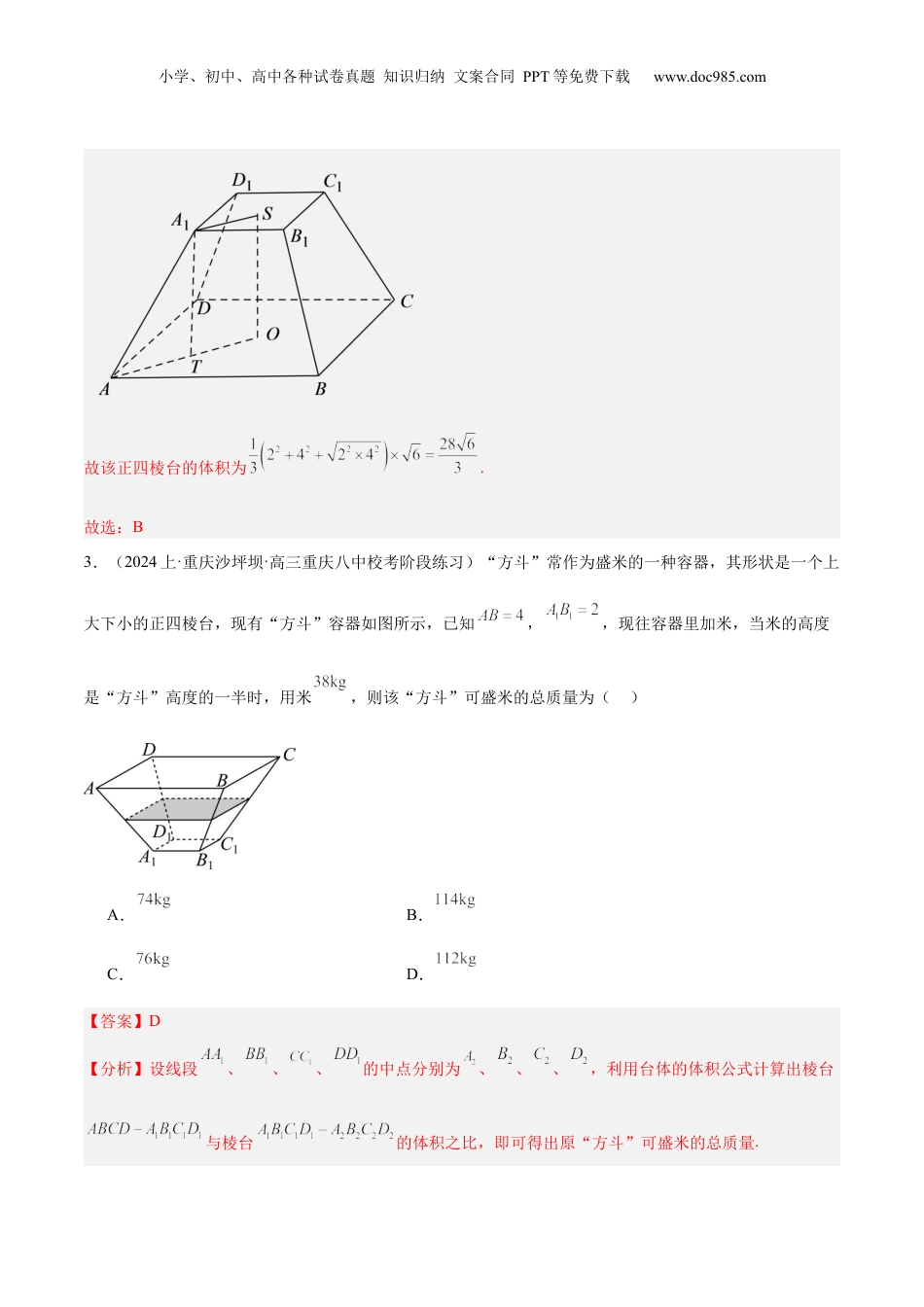
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题验收评价专题5空间向量与立体几何内容概览A·常考题不丢分题型一多面体结构及表面积体积问题题型二多面体内接外切问题题型三空间几何体角度问题题型四空间几何体动点问题C·挑战真题争满分一、单选题1．（2024上·山西运城·高三校考期末）如图所示的粮仓可以看成圆柱体与圆锥体的组合体，设圆锥部分的高为0.5米，圆柱部分的高为2米，底面圆的半径为1米，则该组合体体积为（）A．立方米B．立方米多面体结构及表面积体积问题题型一小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC．立方米D．立方米【答案】D【分析】根据圆柱和圆锥的体积公式可得.【详解】圆柱体积为，圆锥体积为，所以，该组合体的体积为.故选：D2．（2024上·山东淄博·高三统考期末）已知正四棱台的上、下底面边长分别为2和4，若侧棱与底面ABCD所成的角为，则该正四棱台的体积为（）A．B．C．D．【答案】B【详解】如图，分别为上底面和下底面的中心，连接，则⊥底面，过点作⊥于点，则⊥底面，因为上、下底面边长分别为2和4，所以，故，，，由于，故，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com故该正四棱台的体积为.故选：B3．（2024上·重庆沙坪坝·高三重庆八中校考阶段练习）“方斗”常作为盛米的一种容器，其形状是一个上大下小的正四棱台，现有“方斗”容器如图所示，已知，，现往容器里加米，当米的高度是“方斗”高度的一半时，用米，则该“方斗”可盛米的总质量为（）A．B．C．D．【答案】D【分析】设线段、、、的中点分别为、、、，利用台体的体积公式计算出棱台与棱台的体积之比，即可得出原“方斗”可盛米的总质量.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【详解】设线段、、、的中点分别为、、、，如下图所示：易知四边形为等腰梯形，因为线段、的中点分别为、，则，设棱台的高为，体积为，则棱台的高为，设其体积为，则，则，所以，，所以，该“方斗”可盛米的总质量为.故选：D.4．（2024上·山西·高三期末）如图，玛雅金字塔是世界上最大的金字塔之一，同埃及金字塔不同，它的每个侧面都是等腰梯形，并且梯形两腰延长得到的三角形是一个呈“金”字的等边三角形，它的底面是边长为的正方形，塔高为．该金字塔的体积约为（）．（参考数据，）A．120064B．40977C．34048D．31659小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【答案】B【详解】如下图，将金字塔的每个侧面的腰延长得到一个正四棱锥，其中，分别是金字塔的上，下底面，为塔高，点为的中点，连接交于点，由题意知，，则，则在等边三角形中，有，，又，得，即，解得，所以，即金字塔的上底面的边长为，所以金字塔的体积约为．故选：B．5．（2024上·河北廊坊·高三河北省文安县第一中学校联考期末）如图所示，正四棱台中，上底面边长为3，下底面边长为6，体积为，点在上且满足，过点的平面与平面平行，且与正四棱台各面相交得到截面多边形，则该截面多边形的周长为（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．【答案】D【详解】如图所示，过点作于点，因为，所以，则四棱台的高为，则四棱台的体积为，解得，所以侧棱长为.如图所示：过于点，于点，连接，由对称性可知，所以，而，所以，所以，同理，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com分别在棱上取点，使得，易得，所以截面多边形的周长为.故选：D.6．（2024·江西赣州·南康中学校联考一模）在菱形中，，将沿对角线折起，使点A到达的位置，且二面角为直二面角，则三棱锥的外接球的表面积为（）A．B．C．D．【答案】C【分析】根据给定条件，确定三棱锥的外接球的球心位置，再求出球半径即可计算作答.【详解】如图所示：由题意在菱形中，互相垂直且平分，点为垂足，，由勾股定理得，所以，即是等边三角形，，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com设点...