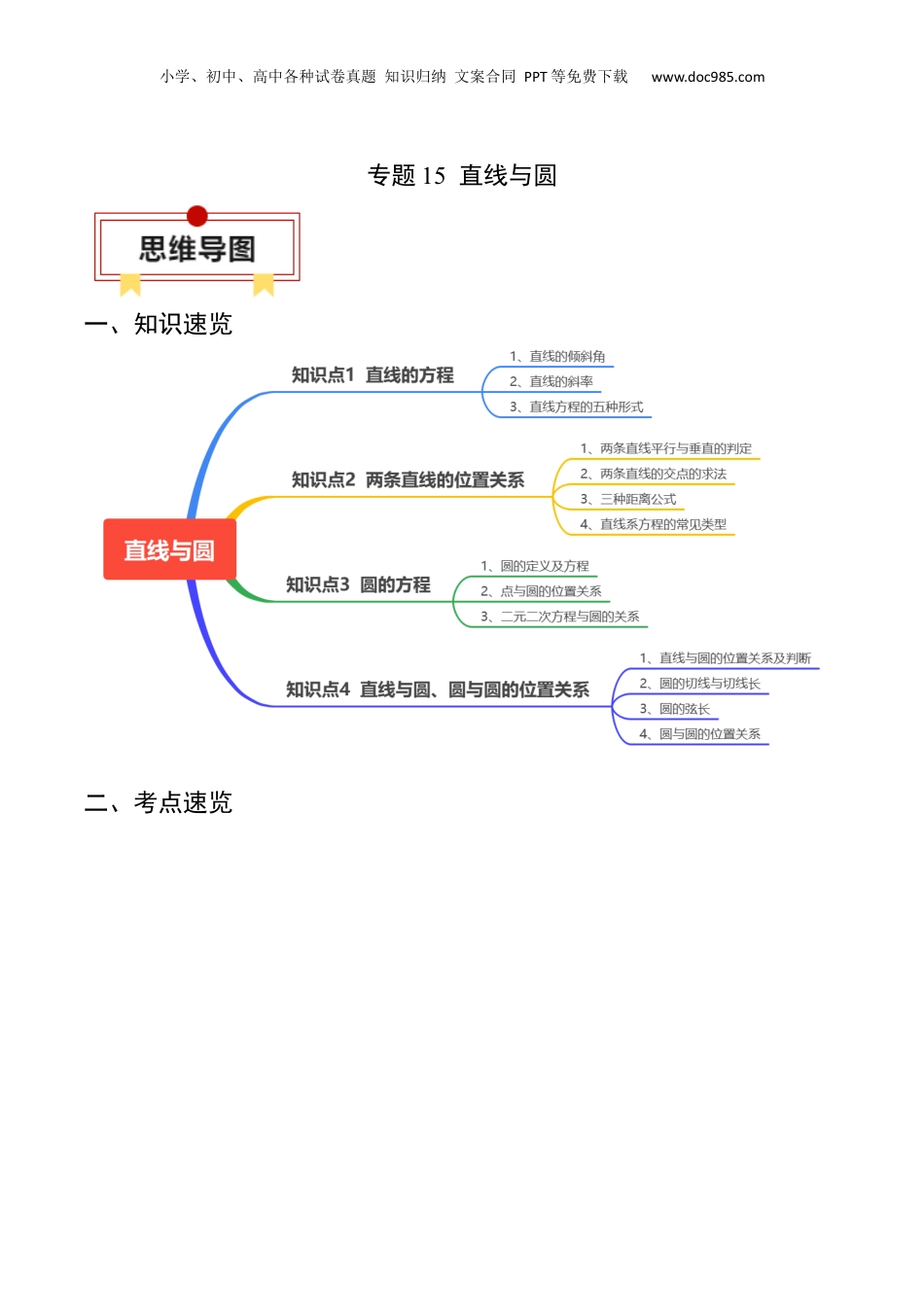
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题15直线与圆一、知识速览二、考点速览小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com知识点1直线的方程1、直线的倾斜角(1)定义:当直线l与x轴相交时,取x轴作为基准,x轴正向与直线l向上方向之间所成的角叫做直线l的倾斜角.当直线l与x轴平行或重合时,规定它的倾斜角为0.(2)范围:直线l倾斜角的取值范围是[0,π).2、直线的斜率(1)定义:一条直线的倾斜角α的正切值叫做这条直线的斜率,斜率常用小写字母k表示,即k=tan_α,倾斜角是的直线没有斜率.(2)过两点的直线的斜率公式:经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式为k=.3、直线方程的五种形式形式几何条件方程适用范围点斜式过一点(x0,y0),斜率ky-y0=k(x-x0)与x轴不垂直的直线斜截式纵截距b,斜率ky=kx+b与x轴不垂直的直线两点式过两点(x1,y1),(x2,y2)=与x轴、y轴均不垂直的直线截距式横截距a,纵截距b+=1不含垂直于坐标轴和过原点的直线小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com一般式Ax+By+C=0(A2+B2≠0)平面直角坐标系内所有直线【注意】“截距”是直线与坐标轴交点的坐标值,它可正、可负,也可以是零,而“距离”是一个非负数.知识点2两条直线的位置关系1、两条直线平行与垂直的判定(1)两条直线平行①对于两条不重合的直线l1,l2,若其斜率分别为k1,k2,则有l1∥l2⇔k1=k2.②当直线l1,l2不重合且斜率都不存在时,l1∥l2.(2)两条直线垂直①如果两条直线l1,l2的斜率存在,设为k1,k2,则有l1⊥l2⇔k1·k2=-1.②当其中一条直线的斜率不存在,而另一条直线的斜率为0时,l1⊥l2.2、两条直线的交点的求法直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0(A1,B1,C1,A2,B2,C2为常数),则l1与l2的交点坐标就是方程组的解.3、三种距离公式(1)平面上的两点P1(x1,y1),P2(x2,y2)间的距离公式|P1P2|=.特别地,原点O(0,0)与任一点P(x,y)的距离|OP|=.(2)点P(x0,y0)到直线l:Ax+By+C=0的距离d=.(3)两条平行线Ax+By+C1=0与Ax+By+C2=0间的距离d=.4、直线系方程的常见类型(1)过定点P(x0,y0)的直线系方程是:y-y0=k(x-x0)(k是参数,直线系中未包括直线x=x0),也就是平常所提到的直线的点斜式方程;(2)平行于已知直线Ax+By+C=0的直线系方程是:Ax+By+λ=0(λ是参数且λ≠C);(3)垂直于已知直线Ax+By+C=0的直线系方程是:Bx-Ay+λ=0(λ是参数);(4)过两条已知直线l1:A1x+B1y+C1=0和l2:A2x+B2y+C2=0的交点的直线系方程是:A1x+B1y+C1+λ(A2x+B2y+C2)=0(λ∈R,但不包括l2).知识点3圆的方程1、圆的定义及方程定义平面内到定点的距离等于定长的点的轨迹叫做圆标准方程(x-a)2+(y-b)2=r2(r>0)圆心:(a,b)半径:r一般方程x2+y2+Dx+Ey+F=0(D2+E2-4F>0)圆心:半径:r=2、点与圆的位置关系点M(x0,y0),圆的标准方程(x-a)2+(y-b)2=r2.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com理论依据点到圆心的距离与半径的大小关系三种情况(x0-a)2+(y0-b)2r2⇔点在圆上(x0-a)2+(y0-b)2r2⇔点在圆外(x0-a)2+(y0-b)2r2⇔点在圆内3、二元二次方程与圆的关系不要把形如x2+y2+Dx+Ey+F=0的结构都认为是圆,一定要先判断D2+E2-4F的符号,只有大于0时才表示圆.若x2+y2+Dx+Ey+F=0表示圆,则有:(1)当F=0时,圆过原点.(2)当D=0,E≠0时,圆心在y轴上;当D≠0,E=0时,圆心在x轴上.(3)当D=F=0,E≠0时,圆与x轴相切于原点;E=F=0,D≠0时,圆与y轴相切于原点.(4)当D2=E2=4F时,圆与两坐标轴相切.知识点4直线与圆、圆与圆的位置关系1、直线与圆的位置关系及判断(1)三种位置关系:相交、相切、相离.(2)两种判断方法:①――――――――――――――――→②――――――――――――→2、圆的切线与切线长(1)过圆上一点的圆的切线①过圆x2+y2=r2上一点M(x0,y0)的切线方程是x0x+y0y=r2.②过圆...