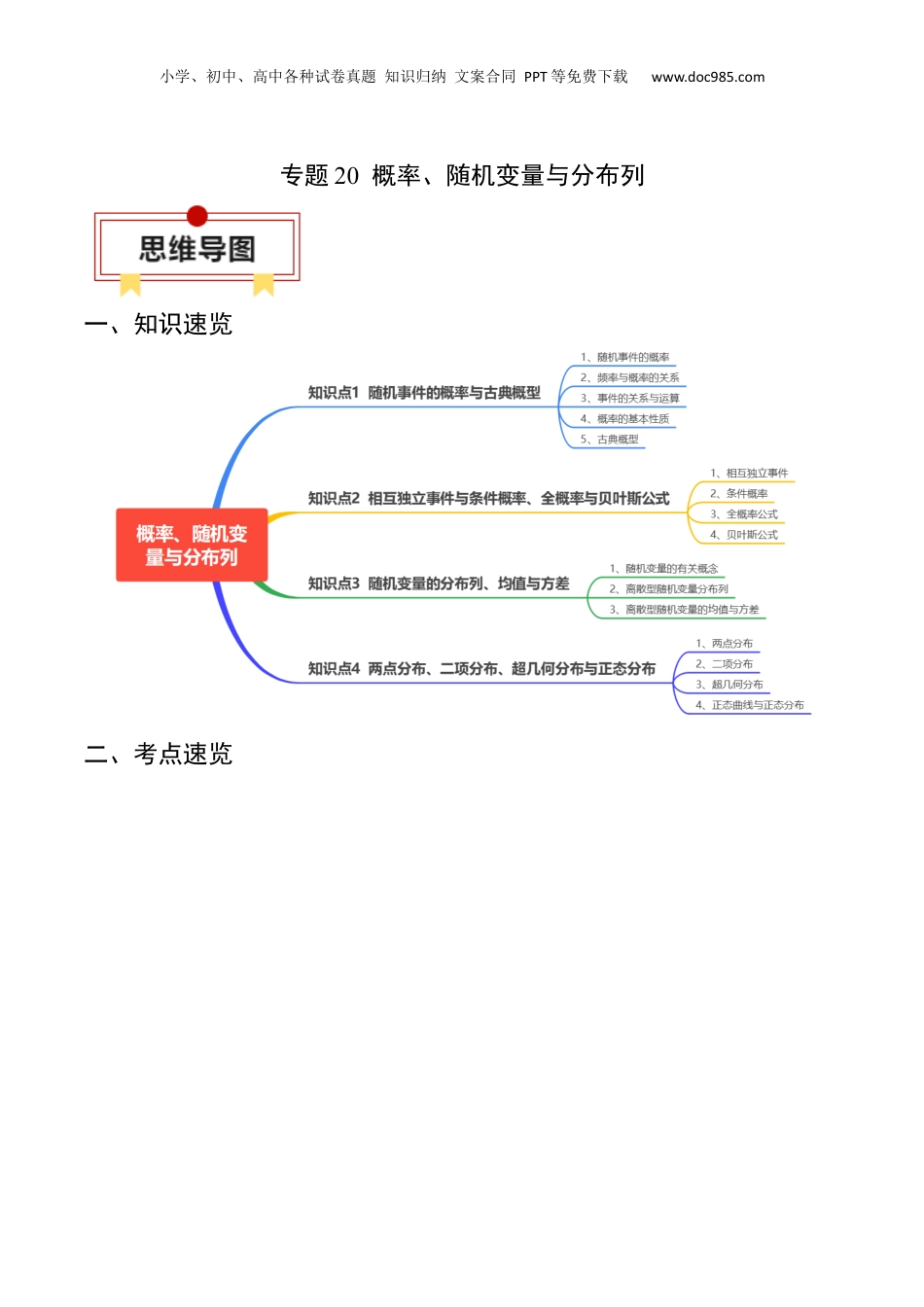
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题20概率、随机变量与分布列一、知识速览二、考点速览小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com知识点1随机事件的概率与古典概型1、事件的相关概念2、频率与概率的关系(1)频率:在次重复试验中,事件发生的次数称为事件发生的频数,频数与总次数的比值,叫做事件发生的频率.(2)概率:在大量重复尽心同一试验时,事件发生的频率总是接近于某个常数,并且在它附近摆动,这时,就把这个常数叫做事件的概率,记作.(3)概率与频率的关系:对于给定的随机事件,由于事件发生的频率随着试验次数的增加稳定于概率,因此可以用频率来估计概率.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com3、事件的关系与运算(1)包含关系:一般地,对于事件和事件,如果事件发生,则事件一定发生,这时称事件包含事件(或者称事件包含于事件),记作或者.(2)相等关系:一般地,若且,称事件与事件相等.(3)并事件(和事件):若某事件发生当且仅当事件发生或事件发生,则称此事件为事件与事件的并事件(或和事件),记作(或).(4)交事件(积事件):若某事件发生当且仅当事件发生且事件发生,则称此事件为事件A与事件B的交事件(或积事件),记作(或).(5)互斥事件:在一次试验中,事件和事件不能同时发生,即,则称事件与事件互斥;如果,,…,中任何两个都不可能同时发生,那么就说事件,..,…,彼此互斥.(6)对立事件:若事件和事件在任何一次实验中有且只有一个发生,即不发生,则称事件和事件互为对立事件,事件的对立事件记为.4、概率的基本性质(1)对于任意事件都有:.(2)必然事件的概率为,即;不可能事概率为,即.(3)概率的加法公式:若事件与事件互斥,则.推广:一般地,若事件,,…,彼此互斥,则事件发生(即,,…,中有一个发生)的概率等于这个事件分别发生的概率之和,即:.(4)对立事件的概率:若事件与事件互为对立事件,则,,且.(5)概率的单调性:若,则.(6)若,是一次随机实验中的两个事件,则.5、古典概型(1)古典概型的定义:一般地,若试验具有以下特征:①有限性:样本空间的样本点只有有限个;②等可能性:每个样本点发生的可能性相等.称试验E为古典概型试验,其数学模型称为古典概率模型,简称古典概型.2、古典概型的概率公式:一般地,设试验是古典概型,样本空间包含个样本点,事件包含其中的个样本点,则定义事件的概率.知识点2相互独立事件与条件概率、全概率小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1、相互独立事件(1)相互独立事件的概念对于两个事件,,如果,则意味着事件的发生不影响事件发生的概率.设,根据条件概率的计算公式,,从而.由此可得:设,为两个事件,若,则称事件与事件相互独立.(2)概率的乘法公式:由条件概率的定义,对于任意两个事件与,若,则.我们称上式为概率的乘法公式.(3)相互独立事件的性质:如果事件,互相独立,那么与,与,与也都相互独立.(4)两个事件的相互独立性的推广:两个事件的相互独立性可以推广到个事件的相互独立性,即若事件,,…,相互独立,则这个事件同时发生的概率.2、条件概率(1)条件概率的定义:一般地,设,为两个事件,且,称为在事件发生的条件下,事件发生的条件概率.(2)条件概率的性质①条件概率具有概率的性质,任何事件的条件概率都在和1之间,即.②必然事件的条件概率为1,不可能事件的条件概率为.③如果与互斥,则.3、全概率公式(1)全概率公式:;小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(2)若样本空间中的事件,,…,满足:①任意两个事件均互斥,即,,;②;③,.则对中的任意事件,都有,且.4、贝叶斯公式(1)一般地,当且时,有(2)定理若样本空间中的事件满足:①任意两个事件均互斥,即,,;②;③,.则对中的任意概率非零的事件,都有,且知识点3随机变量的分布列、均值与方差1、随机变量的有关概念...