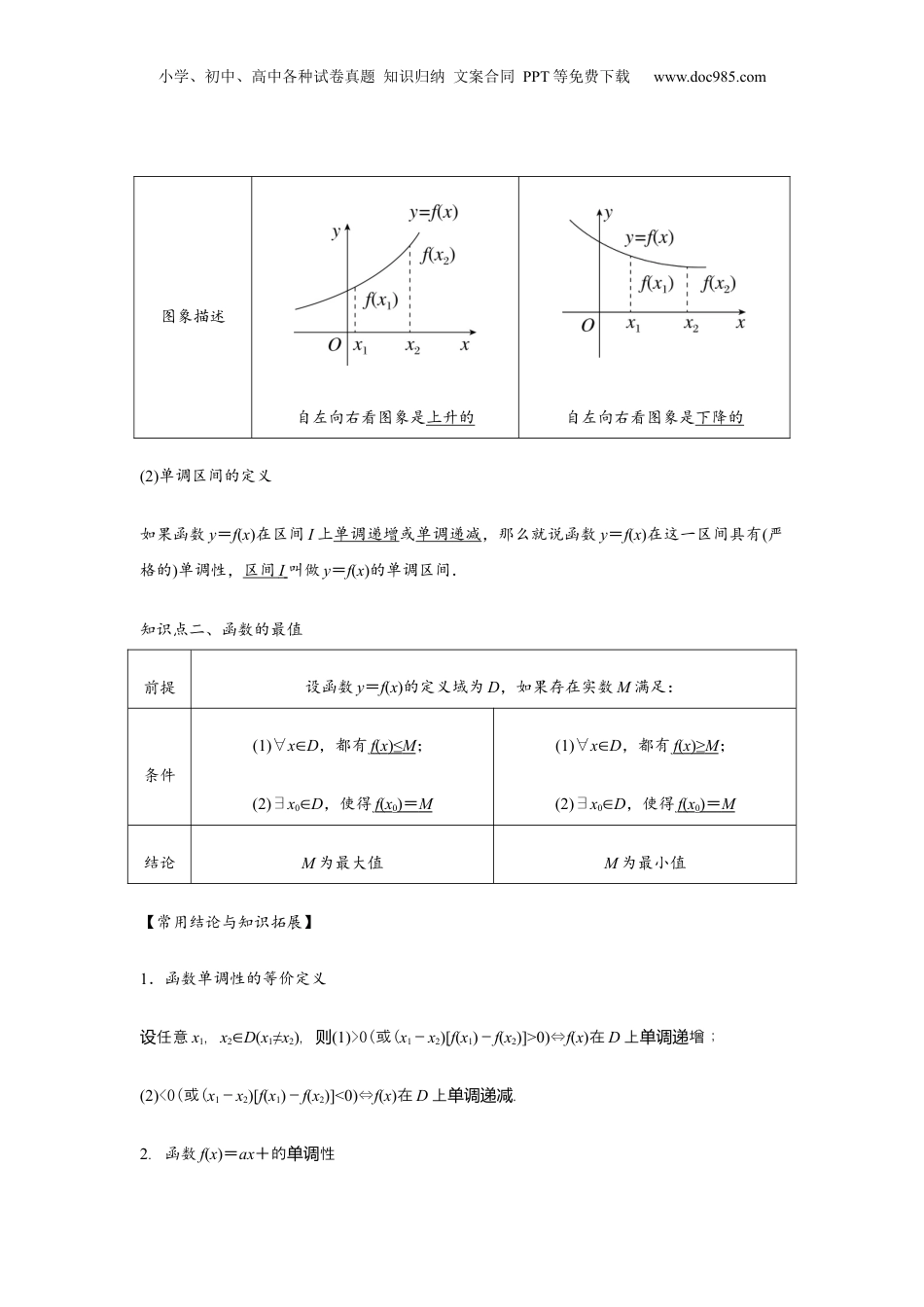
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题02函数的单调性与最值目录题型一：求单调区间...........................................................4题型二：判断函数的单调性.....................................................8题型三：函数单调性的应用——比较大小........................................11题型四：函数单调性的应用——解不等式........................................13题型五：函数单调性的应用——求参数..........................................16题型六：函数单调性的应用——求最值..........................................17知识点一、函数的单调性(1)单调函数的定义增函数减函数定义一般地，设函数f(x)的定义域为D，如果对于定义域D内某个区间I上的任意两个自变量的值x1，x2当x1<x2时，都有f(x1)<f(x2)，那么就称函数f(x)在区间I上单调递增．特别地，当函数f(x)在它的定义域上单调递增时，我们就称它是增函数当x1<x2时，都有f(x1)>f(x2)，那么就称函数f(x)在区间I上单调递减．特别地，当函数f(x)在它的定义域上单调递减时，我们就称它是减函数知识点总结小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com图象描述自左向右看图象是上升的自左向右看图象是下降的(2)单调区间的定义如果函数y＝f(x)在区间I上单调递增或单调递减，那么就说函数y＝f(x)在这一区间具有(严格的)单调性，区间I叫做y＝f(x)的单调区间．知识点二、函数的最值前提设函数y＝f(x)的定义域为D，如果存在实数M满足：条件(1)∀x∈D，都有f(x)≤M；(2)∃x0∈D，使得f(x0)＝M(1)∀x∈D，都有f(x)≥M；(2)∃x0∈D，使得f(x0)＝M结论M为最大值M为最小值【常用结论与知识拓展】1．函数单调性的等价定义任意设x1，x2∈D(x1≠x2)，则(1)>0(或(x1－x2)[f(x1)－f(x2)]>0)⇔f(x)在D上增；单调递(2)<0(或(x1－x2)[f(x1)－f(x2)]<0)⇔f(x)在D上．单调递减2．函数f(x)＝ax＋的性单调小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com若a>0，b<0，函在则数区间(－∞，0)，(0，＋∞)上是增函，若数a<0，b>0，函在则数区间(－∞，0)，(0，＋∞)上是函；若减数a>0，b>0，函在则数区间，上是函，在，减数区间上是增函．数特地，别“勾函对数”y＝x＋(a>0)的增单调递区间为(－∞，－)，(，＋∞)；单调递减区是间[－，0)，(0，]．3．与函数运算有关的单调性结论(1)函数f(x)与f(x)＋c(c常为数)具有相同的性．单调(2)k>0，函时数f(x)与kf(x)性相同；单调k<0，函时数f(x)与kf(x)性相反．单调(3)若f(x)恒正或恒，为值为负值则f(x)与具有相反的性．单调(4)若f(x)，g(x)都是增(减)函，者都恒大于零，数则当两时f(x)·g(x)是增(减)函；者都数当两恒小于零，时f(x)·g(x)是减(增)函．数(5)在公共定域，增＋增＝增，＋＝．义内减减减(6)合函性的判方法：若函的性相同，函的合函复数单调断两个简单数单调则这两个数复数增函；若函的性相反，函的合函函．为数两个简单数单调则这两个数复数为减数简称“同增异减”．题型一：求单调区间【要点讲解】(1)图象法:如果f(x)是以图象给出的,或者f(x)的图象易作出,可由函数图象直观地写出它的单调区间.【例1】函数的单调递减区间为A．B．C．D．例题精讲小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【解答】解：，由题意令，由，解得：，故选：．【变式训练1】函数的递增区间是，．【解答】解：函数的图象如图所示：数形结合可得函数的增区间为，，故答案为：，．【变式训练2】函数的增区间为．【解答】解：因为函数在上单调递减，在上单调递增，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以函数的单调递增区间为，故答案为：．【变式训练3】函数的单调递减区间为．【解答】解：由，得，函数的定义域为，又内层函数的对称轴方程为，则内函数在上为增函数，且外层函数为定义域内的减函数，故复合函数的单调递减区间为．故答案为：．【变式训练4】函数的单调增区间是，．【解答】解：解，得，或；，解得；...