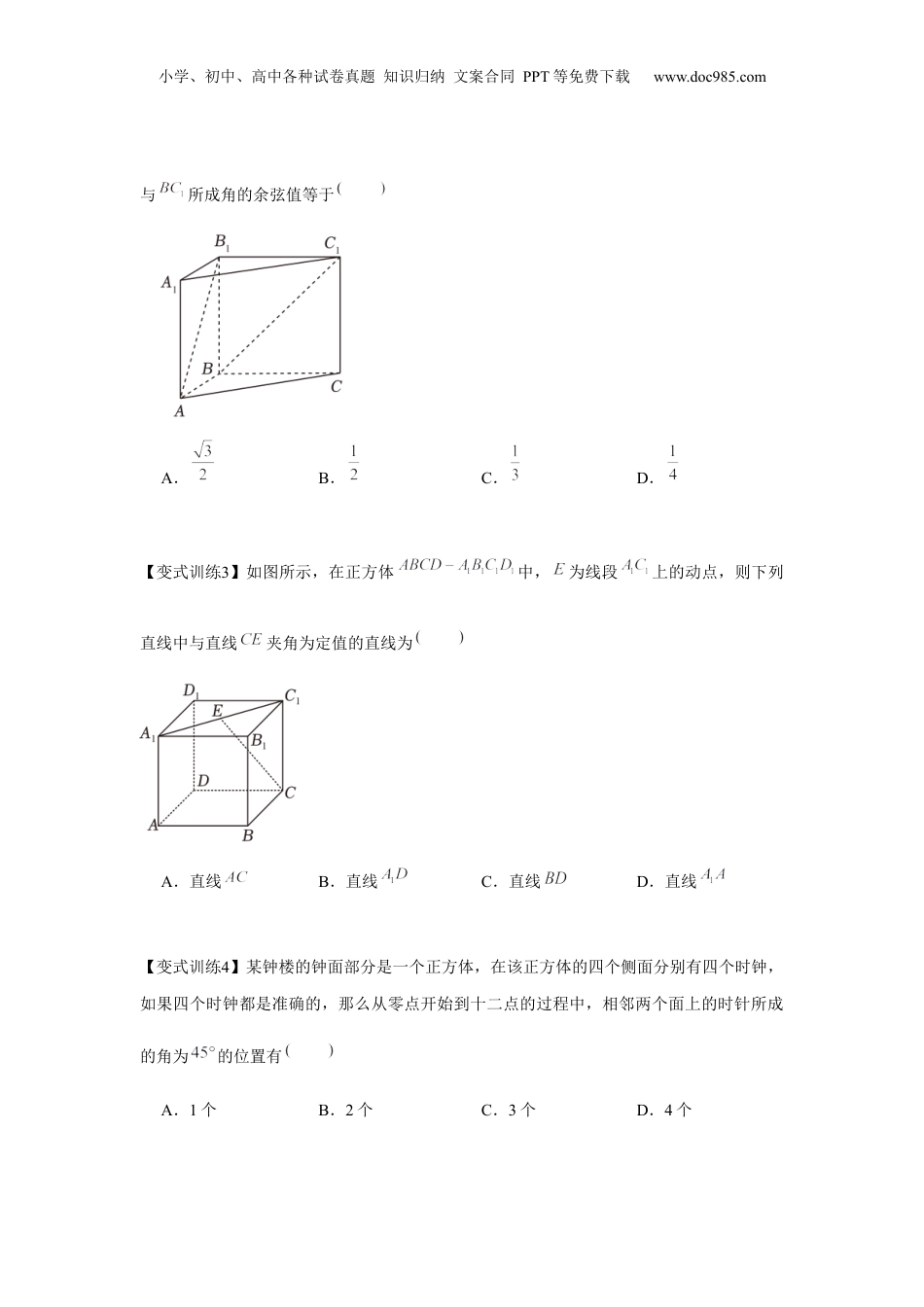
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题7.6向量法求空间角和距离目录题型一：异面直线所成角............................................................................................................2题型二：直线与平面所成角.........................................................................................................4题型三：平面与平面的夹角.........................................................................................................7题型四：点到平面的距离...........................................................................................................11知识点一、用空间向量研究距离、夹角问题分类图示计算公式夹角异面直线所成的角cosθ＝|cos〈u，v〉|＝＝直线与平面所成的角sinθ＝|cos〈u，n〉|＝＝两个平面的夹角cosθ＝|cos〈n1，n2〉|＝＝知识点总结小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com距离点到直线的距离PQ＝＝(u是直线l的单位方向向量)点到平面的距离PQ＝＝＝(n是平面α的法向量)题型一：异面直线所成角【要点讲解】找出两条异面直线的方向向量，结合数量积的运算，利用向量的夹角公式和异面直线所成角的范围即可求得答案．【例1】在长方体中，已知，点是线段的中点，则异面直线与所成角的余弦值为A．B．C．D．【变式训练1】在正方体中，点在上运动（包括端点），则与所成角的取值范围是A．B．C．D．【变式训练2】如图，在直三棱柱中，，则异面直线例题精讲小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com与所成角的余弦值等于A．B．C．D．【变式训练3】如图所示，在正方体中，为线段上的动点，则下列直线中与直线夹角为定值的直线为A．直线B．直线C．直线D．直线【变式训练4】某钟楼的钟面部分是一个正方体，在该正方体的四个侧面分别有四个时钟，如果四个时钟都是准确的，那么从零点开始到十二点的过程中，相邻两个面上的时针所成的角为的位置有A．1个B．2个C．3个D．4个小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【变式训练5】正方体中，，分别是，的中点，则异面直线与所成角的余弦值为A．B．C．D．题型二：直线与平面所成角【要点讲解】利用空间向量求直线与平面所成的角，可以有两种方法：①通过平面的法向量来求，即求出斜线的方向向量与平面的法向量所夹的锐角，取其余角就是斜线和平面所成的角；②分别求出斜线和它在平面内的射影的方向向量，再转化为求这两个方向向量的夹角(或其补角).注意：直线与平面所成角的取值范围是.【例2】如图，在直三棱柱中，，，，分别为，的中点．（1）求证：平面；（2）若，求直线与平面所成角的余弦值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【变式训练1】如图，在三棱台中，是等边三角形，，，侧棱平面，点是棱的中点，点是棱上的动点（不含端点．（1）证明：平面平面；（2）若平面与平面所成的锐角的余弦值为，试判断点的位置．【变式训练2】如图，在多面体中，四边形是一个矩形，，，，，．（1）求证：平面；（2）若平面平面，求平面与平面的夹角的余弦值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【变式训练3】如图，已知在四棱锥中，平面，点在棱上，且，底面为直角梯形，，分别是，的中点．（1）求证：平面；（2）求直线与平面所成角的正弦值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【变式训练4】如图，在三棱锥中，，平面平面，平面平面，，，为的中点．（1）证明：平面．（2）求二面角的余弦值．【变式训练5】如图，在四棱锥中，平面，底面为正方形，为线段的中点，．（Ⅰ）求证：；（Ⅱ）求平面与平面夹角的余弦值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com题型三：平面与平面的夹角【要点讲解】解决平面与平面的夹角问题通常用向量法，具体步骤如下：(1...