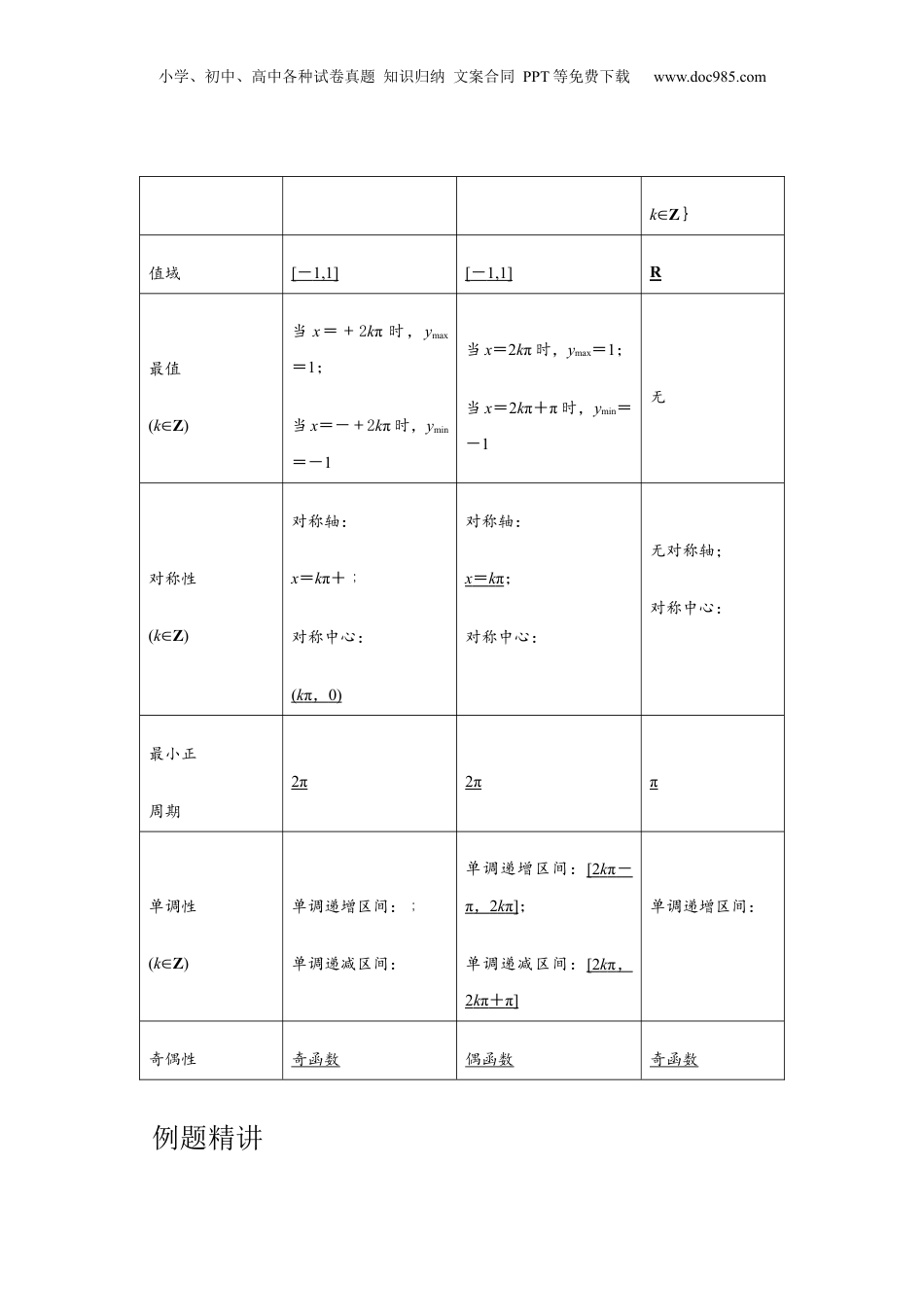
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题05三角函数的图象与性质目录题型一：三角函数的定义域.........................................................................................................3题型二：三角函数的值域............................................................................................................5题型三：三角函数的单调性.........................................................................................................8题型四：三角函数的周期性、对称性、奇偶性.......................................................................10题型五：综合运用......................................................................................................................15知识点一、“五点法”作图(1)在确定正弦函数y＝sinx在[0,2π]上的图象形状时，起关键作用的五个点是(0,0)，，(π，0)，，(2π，0)．(2)在确定余弦函数y＝cosx在[－π，π]上的图象形状时，起关键作用的五个点是(－π，－1)，，(0,1)，，(π，－1)．知识点二、三角函数的图象和性质函数性质y＝sinxy＝cosxy＝tanx图象(一个周期)定义域RR｛x|x≠kπ＋，知识点总结小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comk∈Z｝值域[－1,1][－1,1]R最值(k∈Z)当x＝＋2kπ时，ymax＝1；当x＝－＋2kπ时，ymin＝－1当x＝2kπ时，ymax＝1；当x＝2kπ＋π时，ymin＝－1无对称性(k∈Z)对称轴：x＝kπ＋；对称中心：(kπ，0)对称轴：x＝kπ；对称中心：无对称轴；对称中心：最小正周期2π2ππ单调性(k∈Z)单调递增区间：；单调递减区间：单调递增区间：[2kπ－π，2kπ]；单调递减区间：[2kπ，2kπ＋π]单调递增区间：奇偶性奇函数偶函数奇函数例题精讲小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com题型一：三角函数的定义域【要点讲解】根据函数解析式特征列出与三角函数有关的不等式,借助三角函数性质及图象求解.涉及与正切函数有关的定义域,要注意正切函数本身的定义域.【例1】函数的定义域为，且，．【解答】解：函数，，且，，函数的定义域为，且，，，故答案为：，且，，，【变式训练1】（2022春•南阳期末）函数的定义域是．【解答】解：要使函数有意义，需要满足，解得：，即，故答案为．【变式训练2】（2023春•金牛区校级月考）定义域为小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．【解答】解：由题意得，解得，故定义域为．故选：．【变式训练3】求下列函数的定义域：（1）；（2）；（3）．【解答】解：（1）要使有意义，可得，解得，；（2）要使有意义，可得，即：，解得，；（3）要使有意义，可得．所以函数的定义域为：，．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com题型二：三角函数的值域【要点讲解】(1)求解形如或可化为或的值域,先求出的范围,再结合三角函数的性质求最值.(2)形如或可化为的函数值域问题,可以通过换元转化为二次函数最值问题.(3)形如或可化为,其中f(x),g(x)为正、余弦函数,常将已知条件式变形后,利用正、余弦函数的有界性求解;(4)形如的三角函数,可先设,化为关于t的二次函数再求值域(最值).【例2】（2022秋•南关区校级期末）函数的值域是A．，B．C．D．【解答】解：由于函数，在处，函数最大值2，在处，取得最小值为，故可知函数的值域为：，．故选：．【变式训练1】（2023春•郫都区校级期中）若函数的最大值为，则的值等于A．2B．C．0D．【解答】解：由于，所以时，取最大值，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com故，所以．故选：．【变式训练2】（2023春•全南县校级期中）已知函数，任取，记函数在，上的最大值为，最小值为，设，则函数的值域为A．B．C．D．【解答】解：因为，其中，分别是指在区间，上的最大值和最小值，因为的周期，故在区间，的图象与在区间，上的图象完全相同，故...