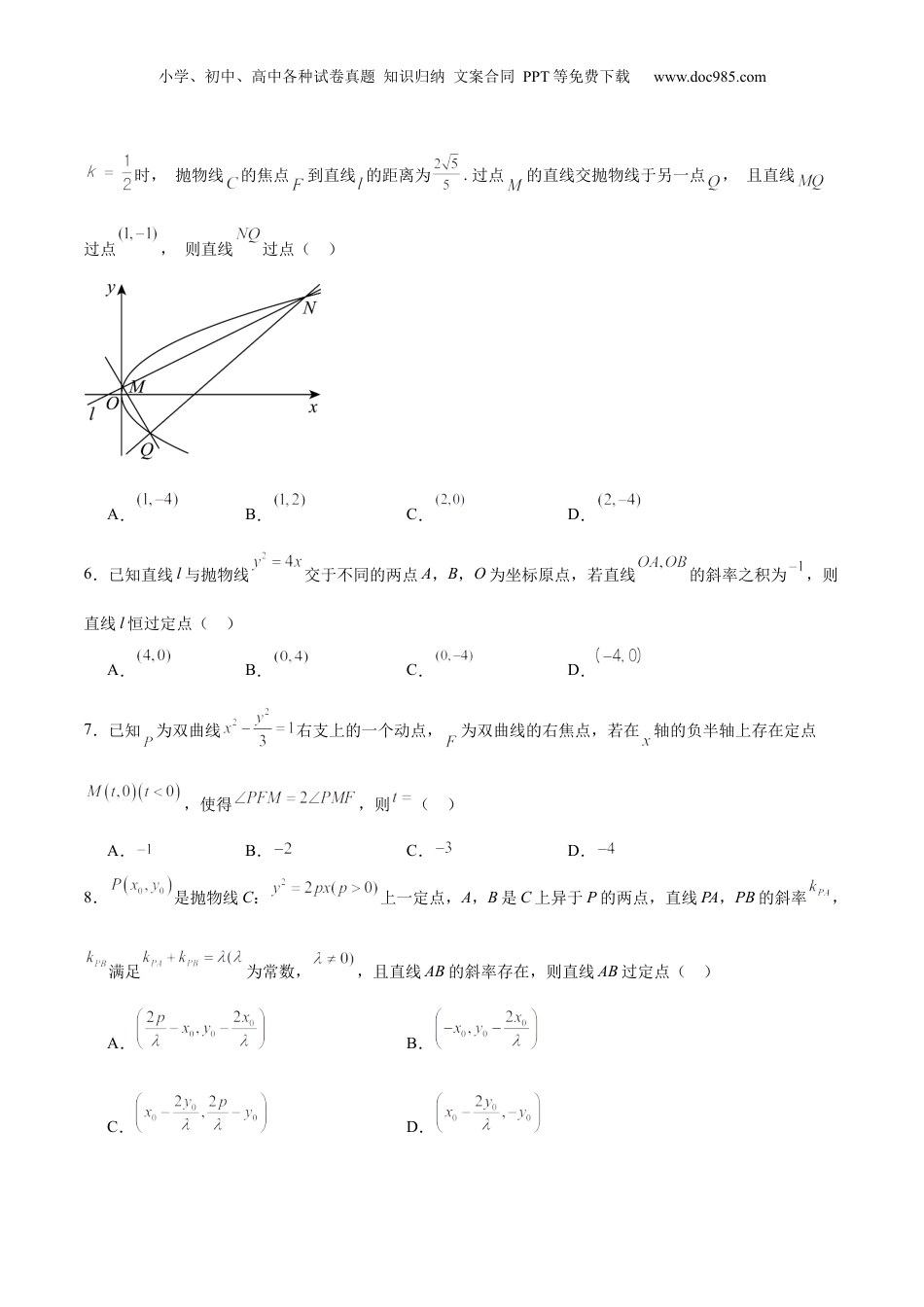
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题29圆锥曲线中的定点问题考试时间：120分钟满分：150分一、单选题：本大题共8小题，每个小题5分，共40分.在每小题给出的选项中，只有一项是符合题目要求的.1．双曲线，过定点的两条垂线分别交双曲线于、两点，直恒过定点（）A．B．C．D．2．已知椭圆为椭圆的右顶点，直线交于两点，且，则恒过除点以外的定点（）A．B．C．D．3．已知椭圆的上顶点为为椭圆上异于A的两点，且，则直线过定点（）A．B．C．D．4．定义：若点在椭圆上，则以为切点的切线方程为：.已知椭圆，点为直线上一个动点，过点作椭圆的两条切线，，切点分别为，，则直线恒过定点（）A．B．C．D．5．如图，设直线与抛物线(为常数)交于不同的两点，且当小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com时，抛物线的焦点到直线的距离为.过点的直线交抛物线于另一点，且直线过点，则直线过点（）A．B．C．D．6．已知直线l与抛物线交于不同的两点A，B，O为坐标原点，若直线的斜率之积为，则直线l恒过定点（）A．B．C．D．7．已知为双曲线右支上的一个动点，为双曲线的右焦点，若在轴的负半轴上存在定点，使得，则（）A．B．C．D．8．是抛物线C：上一定点，A，B是C上异于P的两点，直线PA，PB的斜率，满足为常数，，且直线AB的斜率存在，则直线AB过定点（）A．B．C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com二、多选题：本大题共4小题，每个小题5分，共20分.在每小题给出的选项中，只有一项或者多项是符合题目要求的.9．已知双曲线的两个顶点分别是，两个焦点分别是．P是双曲线上异于的任意一点，则有（）A．B．若，则C．直线的斜率之积等于D．使得为等腰三角形的点P有8个10．已知的左右顶点为为的上顶点，，点为直线上的动点，与的另一个交点为与的另一个交点为.则的方程为（）直线恒过定点（）A．B．C．D．11．已知抛物线：，为坐标原点，直线交抛物线于，两点，若，则（）A．B．直线过定点C．的最小值为D．的最小值为212．已知是抛物线内一动点，直线过点且与抛物线相交于两点，则下列说法正确的是（）A．时，的最小值为B．的取值范围是C．当点是弦的中点时，直线的斜率为D．当点是弦的中点时，轴上存在一定点，都有小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com三、填空题：本大题共4小题，每小题5分，共20分.把答案填在答题卡中的横线上.13．抛物线上有三点，，，直线和的斜率之和为2，则直线恒过定点的坐标为.14．设为椭圆的两个焦点，为上一点，且在第一象限，若为等腰三角形，则的坐标为．15．已知双曲线的一条渐近线的倾斜角的正切值为.若直线（且）与双曲线交于A，B两点，直线，的斜率的倒数和为，则直线恒经过的定点为.16．双曲线的左、右两支上各有一点A、B，点B在直线上的射影是点，若直线AB过右焦点，则直线必定经过的定点的坐标为．四、解答题：本大题共6小题，共70分.解答应写出必要的文字说明、证明过程或演算步骤．17．设椭圆C：的左、右顶点分别为A、B，且焦距为2．点P在椭圆上且异于A、B两点．若直线PA与PB的斜率之积为．(1)求椭圆C的标准方程；(2)过点作不与轴重合的直线与椭圆C相交于M、N两点，直线m的方程为：，过点M作垂直于直线，交于点E．判断直线是否过定点，并说明理由．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com18．已知椭圆E的中心在原点，周长为8的的顶点，为椭圆E的左焦点，顶点B，C在E上，且边BC过E的右焦点.(1)求椭圆E的标准方程；(2)椭圆E的上、下顶点分别为M，N，点若直线，与椭圆E的另一个交点分别为点S，T，证明：直线ST过定点，并求该定点坐标.19．已知椭圆的左顶点，点是椭圆上关于原点对称的两个动点（点不与点重合），面积的最大值是2.(1)求椭圆的方程.(2)若直线与轴分别相交于点，是否存在定点，总有？若存在，求出定点的坐标；若不存在，说明理由.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com20．已知抛物线：，为坐标原点，过作一条直...