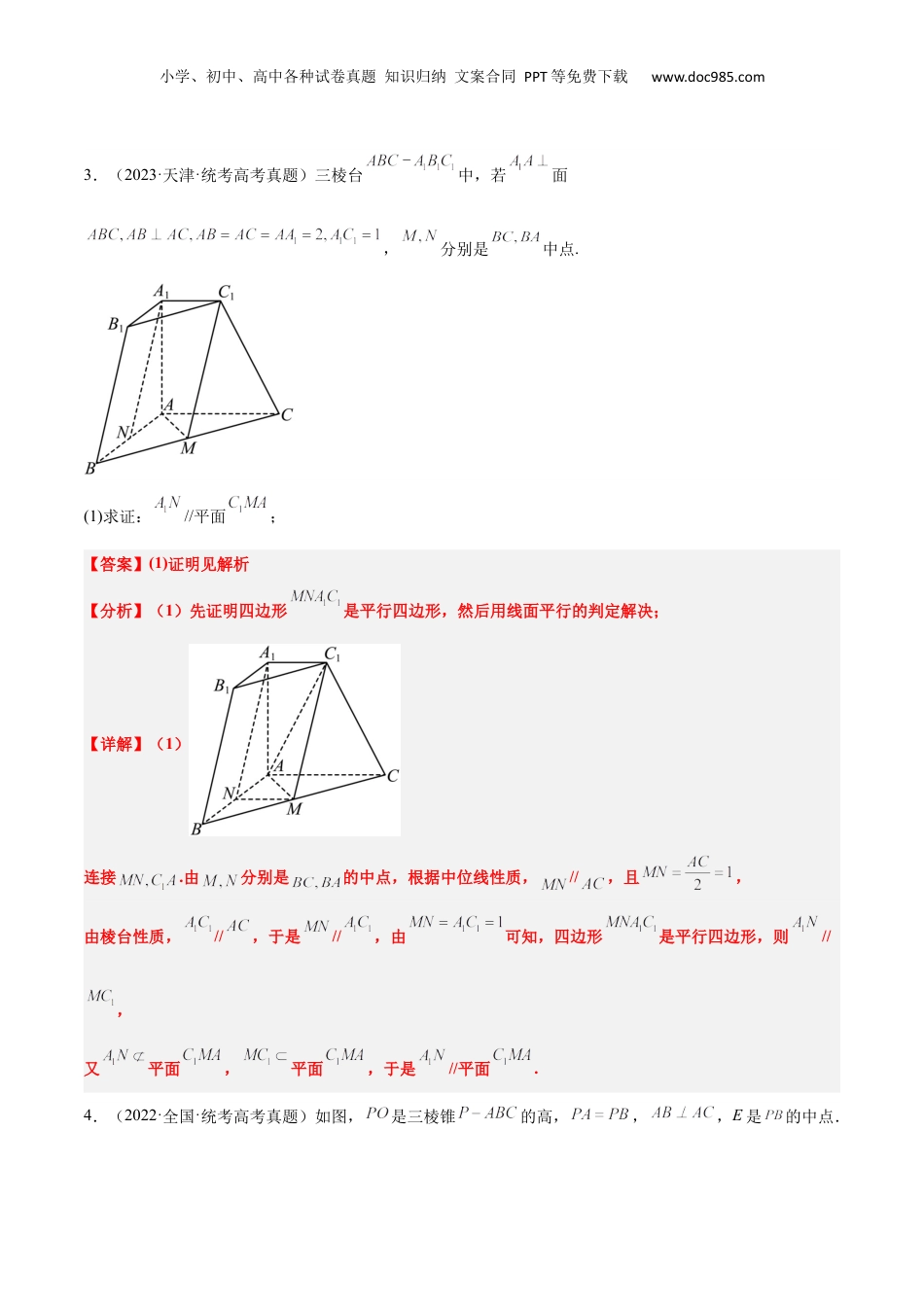
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【一轮复习讲义】2024年高考数学高频考点题型归纳与方法总结（新高考通用）第33练空间直线、平面的平行（精练）一、解答题1．（2023·全国·统考高考真题）如图，在三棱锥中，，，，，的中点分别为，点在上，．(1)求证：//平面；【答案】(1)证明见解析【分析】（1）根据给定条件，证明四边形为平行四边形，再利用线面平行的判定推理作答.【详解】（1）连接，设，则，，，则，解得，则为的中点，由分别为的中点，于是，即，则四边形为平行四边形，，又平面平面，所以平面.刷真题明导向小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2．（2023·全国·统考高考真题）如图，在三棱锥中，，，，，BP，AP，BC的中点分别为D，E，O，，点F在AC上，.(1)证明：平面；【答案】(1)证明见解析；【分析】（1）根据给定条件，证明四边形为平行四边形，再利用线面平行的判定推理作答.【详解】（1）连接，设，则，，，则，解得，则为的中点，由分别为的中点，于是，即，则四边形为平行四边形，，又平面平面，所以平面.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com3．（2023·天津·统考高考真题）三棱台中，若面，分别是中点.(1)求证：//平面；【答案】(1)证明见解析【分析】（1）先证明四边形是平行四边形，然后用线面平行的判定解决；【详解】（1）连接.由分别是的中点，根据中位线性质，//，且，由棱台性质，//，于是//，由可知，四边形是平行四边形，则//，又平面，平面，于是//平面.4．（2022·全国·统考高考真题）如图，是三棱锥的高，，，E是的中点．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)证明：平面；【答案】(1)证明见解析【分析】（1）连接并延长交于点，连接、，根据三角形全等得到，再根据直角三角形的性质得到，即可得到为的中点从而得到，即可得证；【详解】（1）证明：连接并延长交于点，连接、，因为是三棱锥的高，所以平面，平面，所以、，又，所以，即，所以，又，即，所以，，所以所以，即，所以为的中点，又为的中点，所以，又平面，平面，所以平面5．（2022·全国·统考高考真题）小明同学参加综合实践活动，设计了一个封闭的包装盒，包装盒如图所示：底面是边长为8（单位：）的正方形，均为正三角形，且它们所在的平面都与平面垂直．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(1)证明：平面；(2)求该包装盒的容积（不计包装盒材料的厚度）．【答案】(1)证明见解析；(2)．【分析】（1）分别取的中点，连接，由平面知识可知，，依题从而可证平面，平面，根据线面垂直的性质定理可知，即可知四边形为平行四边形，于是，最后根据线面平行的判定定理即可证出；（2）再分别取中点，由（1）知，该几何体的体积等于长方体的体积加上四棱锥体积的倍，即可解出．【详解】（1）如图所示：小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com分别取的中点，连接，因为为全等的正三角形，所以，，又平面平面，平面平面，平面，所以平面，同理可得平面，根据线面垂直的性质定理可知，而，所以四边形为平行四边形，所以，又平面，平面，所以平面．（2）[方法一]：分割法一如图所示：分别取中点，由（1）知，且，同理有，，，，由平面知识可知，，，，所以该几何体的体积等于长方体的体积加上四棱锥体积的倍．因为，，点到平面的距离即为点到直线的距离，，所以该几何体的体积．[方法二]：分割法二如图所示：小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com连接AC,BD,交于O，连接OE,OF,OG,OH.则该几何体的体积等于四棱锥O-EFGH的体积加上三棱锥A-OEH的倍,再加上三棱锥E-OAB的四倍．容易求得，OE=OF=OG=OH=8,取EH的中点P，连接AP,OP.则EH垂直平面APO.由图可知，三角形APO,四棱锥O-EFGH与三棱锥E-OAB的高均为EM的长.所以该几何体的体积6．（2022·北京·统考高考真题）如图，在三棱柱中，侧面为正方形，平面平面，，M，N分别为，AC...