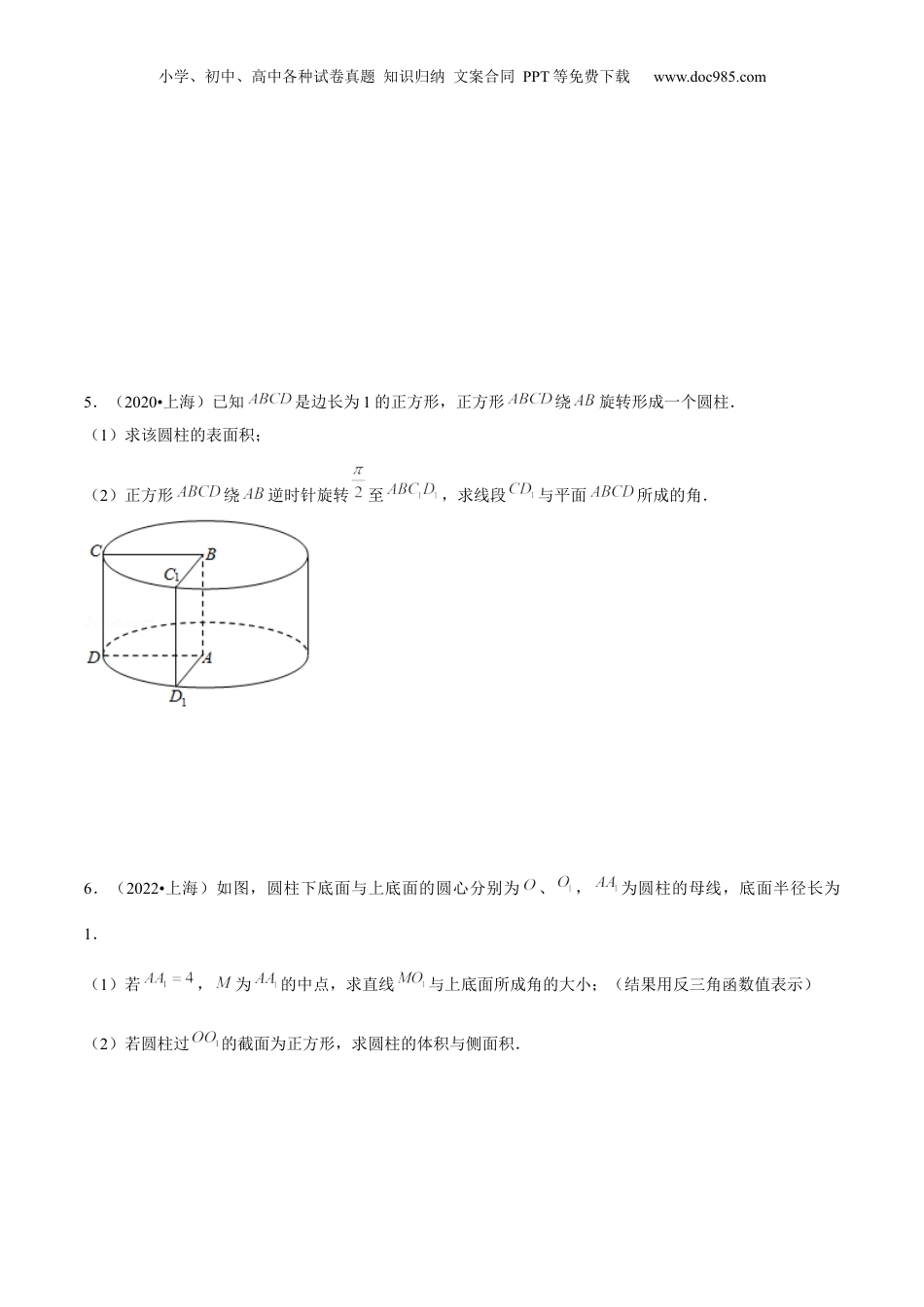
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com押上海高考17题三角函数、立体几何考点4年考题考情分析三角函数2024年春考三角函数周期性立体几何2020年~2023年近四年考查方向求体积、面积，线面、面面平行，线线、线面、面面所成的角一．三角函数的周期性（共1小题）1．（2024•上海）已知，．（1）设，求解：，，的值域；（2），的最小正周期为，若在，上恰有3个零点，求的取值范围．二．棱柱、棱锥、棱台的体积（共2小题）2．（2020•上海）已知四棱锥，底面为正方形，边长为3，平面．（1）若，求四棱锥的体积；（2）若直线与的夹角为，求的长．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com3．（2022•上海）如图所示三棱锥，底面为等边，为边中点，且底面，．（1）求三棱锥体积；（2）若为中点，求与面所成角大小．三．直线与平面所成的角（共4小题）4．（2021•上海）四棱锥，底面为正方形，边长为4，为中点，平面．（1）若为等边三角形，求四棱锥的体积；（2）若的中点为，与平面所成角为，求与所成角的大小．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com5．（2020•上海）已知是边长为1的正方形，正方形绕旋转形成一个圆柱．（1）求该圆柱的表面积；（2）正方形绕逆时针旋转至，求线段与平面所成的角．6．（2022•上海）如图，圆柱下底面与上底面的圆心分别为、，为圆柱的母线，底面半径长为1．（1）若，为的中点，求直线与上底面所成角的大小；（结果用反三角函数值表示）（2）若圆柱过的截面为正方形，求圆柱的体积与侧面积．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com7．（2021•上海）如图，在长方体中，已知，．（1）若是棱上的动点，求三棱锥的体积；（2）求直线与平面的夹角大小．四．二面角的平面角及求法（共1小题）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com8．（2023•上海）已知直四棱柱，，，，，．（1）证明：直线平面；（2）若该四棱柱的体积为36，求二面角的大小．五．点、线、面间的距离计算（共1小题）9．（2023•上海）已知三棱锥中，平面，，，，为中点，过点分别作平行于平面的直线交、于点，．（1）求直线与平面所成角的大小；（2）证明：平面平面，并求直线到平面的距离．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com一、三角函数的周期性(1)正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是周期，相的中心之个邻对称与对称轴的距离是周期．间个(2)正切曲线相邻两对称中心之间的距离是周期．个二．圆柱、圆锥、圆台的侧面展开图及侧面积公式圆柱圆锥圆台侧面展开图侧面积公式S圆柱侧＝2πrlS圆锥侧＝πrlS圆台侧＝π(r1＋r2)l三．柱、锥、台、球的表面积和体积名称几何体表面积体积柱体S表＝S侧＋2S底V＝Sh锥体S表＝S侧＋S底V＝Sh台体S表＝S侧＋S上＋S下V＝(S上＋S下＋)h球S表＝4πR2V＝πR3四．线面平行的判定定理和性质定理文字语言图形语言符号语言判定定理如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行⇒a∥α性质定理一条直线与一个平面平行，如果过该直线的平面与此平面相交，那么该直⇒a∥b小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com线与交线平行五．面面平行的判定定理和性质定理文字语言图形语言符号语言判定定理如果一个平面内的两条相交直线与另一个平面平行，那么这两个平面平行⇒β∥α性质定理两个平面平行，如果另一个平面与这两个平面相交，那么两条交线平行⇒a∥b六．异面直线所成的角(1)定义：已知两条异面直线a，b，经过空间任一点O分别作直线a′∥a，b′∥b，我们把直线a′与b′所成的角叫做异面直线a与b所成的角(或夹角)．(2)范围：.七.直线和平面所成的角(1)定义：平面的一条斜线和它在平面上的射影所成的角，叫做这条直线和这个平面所成的角．一条直线垂直于平面，我们说它们所成的角是90°；一条直线和平面平行，或在平面内，我们说它们所成的角是0°.(2)范围：.八...