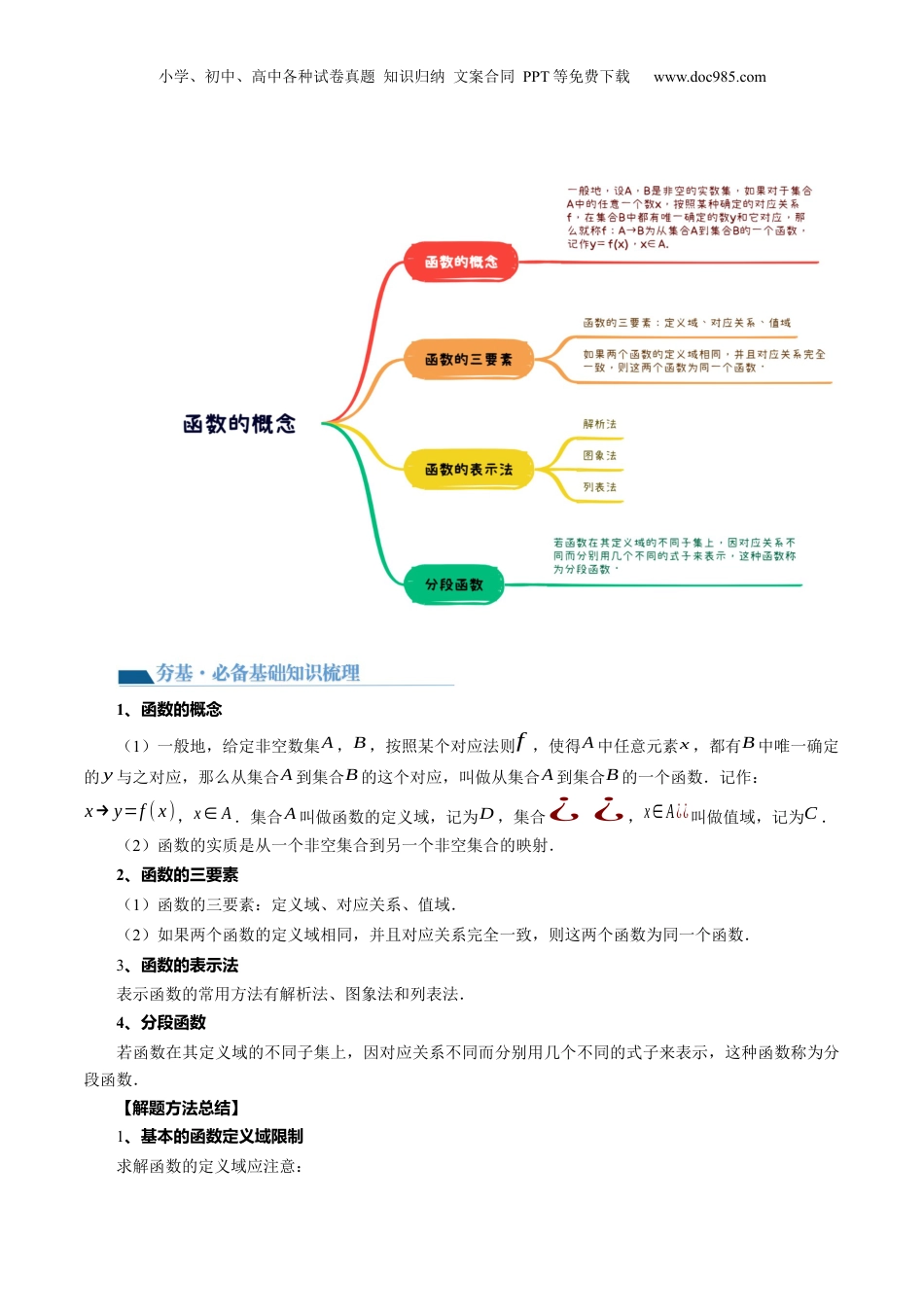
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第01讲函数的概念目录考点要求考题统计考情分析（1）了解函数的含义，会求简单函数的定义域和值域．（2）在实际情景中，会根据不同的需要选择恰当的方法（如图象法、列表法、解析法）表示函数．（3）了解简单的分段函数，并会简单的应用．2022年浙江卷第14题，5分2021年浙江卷第12题，5分高考对集合的考相对定，考内查稳查、率、题型、变化不大．容频难度均高考对本的考不会有大的变化，节查将以分段函数、定义域、值域及最仍值为主，综合考不等式与函数的性查质．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1、函数的概念（1）一般地，给定非空数集A，B，按照某个对应法则f，使得A中任意元素x，都有B中唯一确定的y与之对应，那么从集合A到集合B的这个对应，叫做从集合A到集合B的一个函数．记作：x→y=f(x)，x∈A．集合A叫做函数的定义域，记为D，集合¿¿，x∈A¿¿叫做值域，记为C．（2）函数的实质是从一个非空集合到另一个非空集合的映射．2、函数的三要素（1）函数的三要素：定义域、对应关系、值域．（2）如果两个函数的定义域相同，并且对应关系完全一致，则这两个函数为同一个函数．3、函数的表示法表示函数的常用方法有解析法、图象法和列表法．4、分段函数若函数在其定义域的不同子集上，因对应关系不同而分别用几个不同的式子来表示，这种函数称为分段函数．【解题方法总结】1、基本的函数定义域限制求解函数的定义域应注意：小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（1）分式的分母不为零；（2）偶次方根的被开方数大于或等于零：（3）对数的真数大于零，底数大于零且不等于1；（4）零次幂或负指数次幂的底数不为零；（5）三角函数中的正切的定义域是且；（6）已知的定义域求解的定义域，或已知的定义域求的定义域，遵循两点：①定义域是指自变量的取值范围；②在同一对应法则下，括号内式子的范围相同；∫（7）对于实际问题中函数的定义域，还需根据实际意义再限制，从而得到实际问题函数的定义域．2、基本初等函数的值域（1）y=kx+b(k≠0)的值域是R．（2）y=ax2+bx+c(a≠0)的值域是：当a>0时，值域为{y|y≥4ac−b24a}；当a<0时，值域为{y|y≥4ac−b24a}．（3）y=kx(k≠0)的值域是{y|y≠0}．（4）y=ax(a>0且a≠1)的值域是(0，+∞)．（5）y=logax(a>0且a≠1)的值域是R．题型一函数的概念：例1．（2023·山东潍坊·统考一模）存在函数满足：对任意都有（）A．B．C．D．【答案】D【解析】对于A，当时，；当时，，不符合函数定义，A错误；对于B,令，则，令，则，不符合函数定义，B错误；对于C,令，则，令，则，不符合函数定义，C错误；对于D,,,则，则存在时，，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com符合函数定义，即存在函数满足：对任意都有，D正确，故选：D例2．（2023·重庆·二模）任给，对应关系使方程的解与对应，则是函数的一个充分条件是（）A．B．C．D．【答案】A【解析】根据函数的定义，对任意，按，在的范围中必有唯一的值与之对应，，则，则的范围要包含，故选：A．例3．（2023·全国·高三专题练习）如图，可以表示函数的图象的是（）A．B．C．D．【答案】D【解析】根据函数的定义，对于一个，只能有唯一的与之对应，只有D满足要求故选：D变式1．（2023·全国·高三专题练习）函数y=f(x)的图象与直线的交点个数（）A．至少1个B．至多1个C．仅有1个D．有0个、1个或多个【答案】B【解析】若1不在函数f(x)的定义域内，y=f(x)的图象与直线没有交点，若1在函数f(x)的定义域内，y=f(x)的图象与直线有1个交点，故选：B.【解题方法总结】利用函数概念判断题型一函数的判断二：同小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com例4．（2023·高三课时练习）下列各组函数中，表示同一个函数的是（）．A．，B．，C．，D．，【答案】C【解析】对于A：的定义域为，的定义域为.因为定义域不同，所以和不是同一个函数.故A错误；对于B：的定义域为，的定义域为.因...