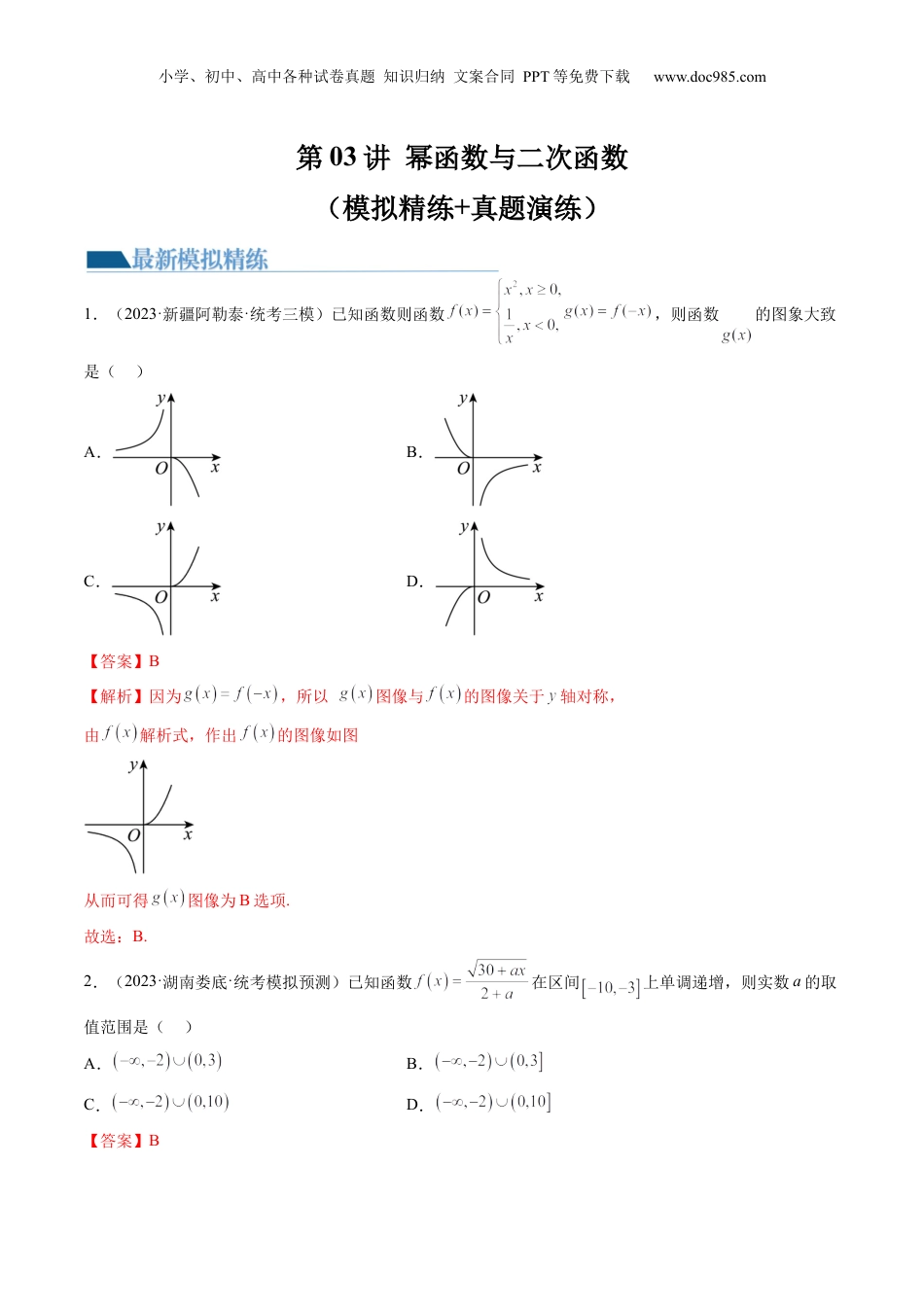
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第03讲幂函数与二次函数（模拟精练+真题演练）1．（2023·新疆阿勒泰·统考三模）已知函数则函数，则函数的图象大致是（）A．B．C．D．【答案】B【解析】因为，所以图像与的图像关于轴对称，由解析式，作出的图像如图从而可得图像为B选项.故选：B.2．（2023·湖南娄底·统考模拟预测）已知函数在区间上单调递增，则实数a的取值范围是（）A．B．C．D．【答案】B小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【解析】因为函数在区间上单调递增，所以且在区间上恒成立，所以，解得或.故选：B3．（2023·海南·模拟预测）已知函数，，的图象如图所示，则（）A．B．C．D．【答案】C【解析】由图象可知：，.故选：C.4．（2023·广东肇庆·校考模拟预测）已知函数，若，则实数的取值范围是（）A．B．C．D．【答案】D【解析】因为开口向下的二次函数，对称轴为，故函数在上单调递减；为开口向上的二次函数，对称轴为，故函数在上单调递减，且，因此函数在R上单调递减，则，即，解得或，所以实数的取值范围是。故选：D小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com5．（2023·北京海淀·一模）设，二次函数的图象为下列之一，则的值为（）A．B．C．D．【答案】B【解析】由题知，，所以二次函数的图象不关于轴对称，故排除第一、二个函数图象，当时，该二次函数的对称轴为，故第四个图象也不满足题意，当时，该二次函数的对称轴为，开口向下，故第三个函数图象满足题意.此时函数图象过坐标原点，故，解得，由于，故.故选：B6．（2023·河南新乡·高三校联考开学考试）已知函数若的最小值为6，则实数a的取值范围是（）A．B．C．D．【答案】C【解析】因为当时，，当且仅当时，等号成立，所以当时，，当时，的最小值大于或等于6.当时，在上单调递减，则.由得；当时，.由得.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com综合可得.故选：C．7．（2023·全国·模拟预测）已知x，，满足，，则（）A．-1B．0C．1D．2【答案】B【解析】令，，则，∴为奇函数． ，∴．又 ，∴，∴，．又 在R上单调递增，∴，即．故选：B．8．（2023·贵州毕节·统考二模）已知，则实数a的取值范围为（）A．B．C．D．【答案】D【解析】，根据指数函数在上单调递减得，，根据幂函数在上单调递增知，则，，根据对数函数在上单调递减得，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com综上.故选：D.9．（多选题）（2023·江苏·校联考模拟预测）若函数，且，则（）A．B．C．D．【答案】AC【解析】由幂函数的性质知，在上单调递增.因为,所以，即，，所以．故A正确；令，则，故B错误；令，则由函数单调性的性质知，在上单调递增，在上单调递增，所以在上单调递增，因为，所以，即，于是有，故C正确；令，则，所以因为，故D错误．故选：AC.10．（多选题）（2023·吉林长春·东北师大附中校考模拟预测）已知幂函数图像经过点，则下列命题正确的有（）A．函数为增函数B．函数为偶函数C．若，则D．若，则【答案】BD【解析】将点代入函数得：，则.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以，显然在定义域上为减函数，所以A错误；，所以为偶函数，所以B正确；当时，，即，所以C错误；当若时，假设，整理得，化简得，，即证明成立，利用基本不等式，，因为，故等号不成立，成立；即成立，所以D正确.故选：BD.11．（多选题）（2023·全国·高三专题练习）已知关于x的方程x2＋(m－3)x＋m＝0，下列结论正确的是（）A．方程x2＋(m－3)x＋m＝0有实数根的充要条件是m{∈m|m<1或m>9}B．方程x2＋(m－3)x＋m＝0有一正一负根的充要条件是m{∈m|m<0}C．方程x2＋(m－3)x＋m＝0有两正实数根的充要条件是m{∈m|0<m≤1}D．方程x2＋(m－3)x＋m＝0无实数根的必要条件是m{∈m|m>1}【答案】BCD【解析】方程x2＋(m－3)x＋m＝0有实数根的充要条件是，解得，A错误；方程x2＋(m－3)x＋m＝0有一正一负根的充要条件是，解得...