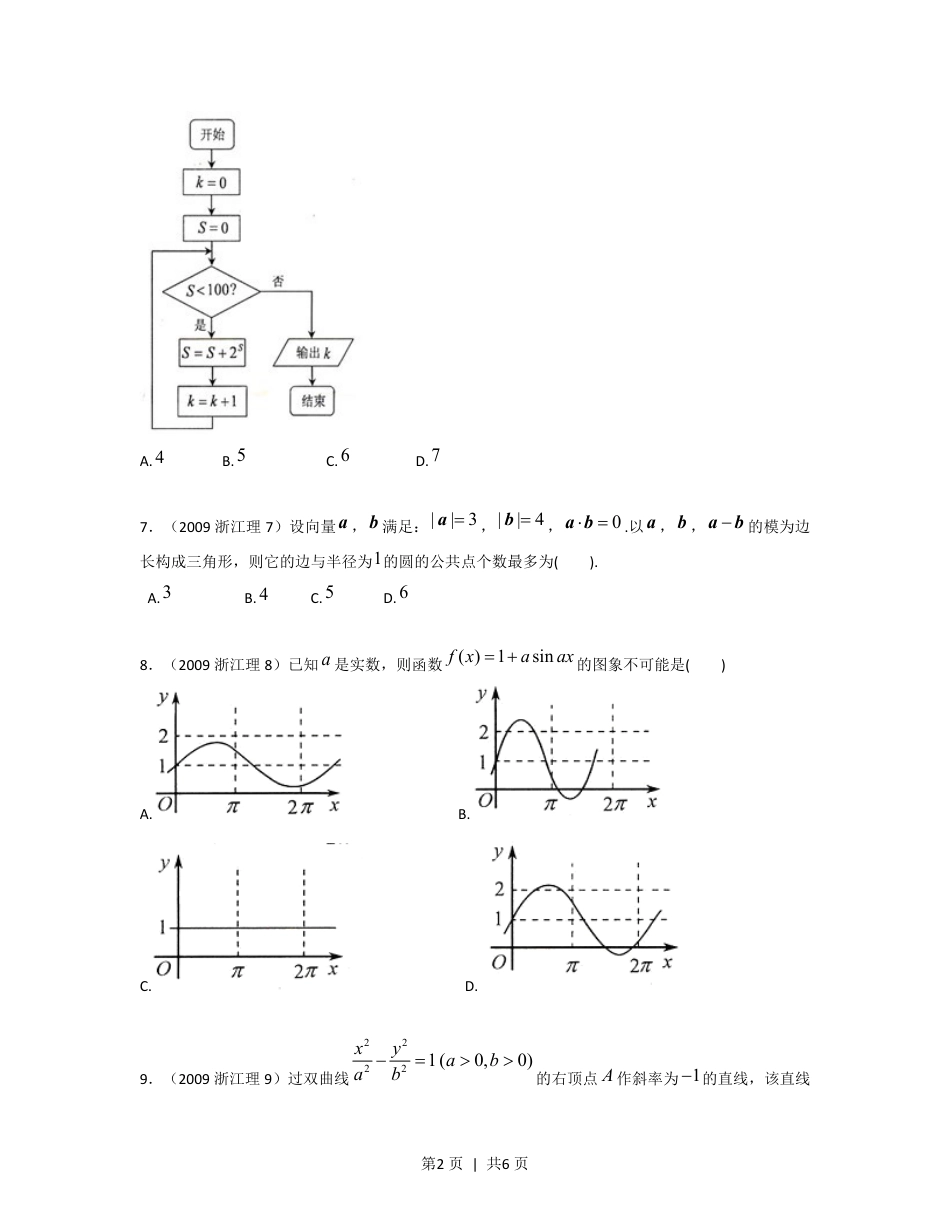
第1页|共6页2009年高考数学浙江理科试卷含详细解答一、选择题（本大题共10小题，共0分）1．（2009浙江理1）设U=R，{|0}Axx=>，{|1}Bxx=>，则UACBÇ=()A.{|01}xx£<B.{|01}xx<£C.{|0}xx<D.{|1}xx>2．（2009浙江理2）已知,ab是实数，则“0a>且0b>”是“0ab+>且0ab>”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件3．（2009浙江理3）设1zi=+（i是虚数单位），则22zz+=()A.1i--B.1i-+C.1i-D.1i+4．（2009浙江理4）在二项式251()xx-的展开式中，含4x的项的系数是().A.10-B.10C.5-D.55．（2009浙江理5）在三棱柱111ABCABC-中，各棱长相等，侧掕垂直于底面，点D是侧面11BBCC的中心，则AD与平面11BBCC所成角的大小是()A.30oB.45oC.60oD.90o6．（2009浙江理6）某程序框图如图所示，该程序运行后输出的k的值是()第2页|共6页A.4B.5C.6D.77．（2009浙江理7）设向量a，b满足：||3=a，||4=b，0×=ab.以a，b，-ab的模为边长构成三角形，则它的边与半径为1的圆的公共点个数最多为().A.3B.4C.5D.68．（2009浙江理8）已知a是实数，则函数()1sinfxaax=+的图象不可能是()A.B.C.D.9．（2009浙江理9）过双曲线22221(0,0)xyabab-=>>的右顶点A作斜率为1-的直线，该直线第3页|共6页与双曲线的两条渐近线的交点分别为,BC.若12ABBC=uuuruuur，则双曲线的离心率是()A.2B.3C.5D.1010．（2009浙江理10）对于正实数a，记Ma为满足下述条件的函数()fx构成的集合：12,xx"ÎR且21xx>，有212121()()()()xxfxfxxxaa--<-<-.下列结论中正确的是()A.若1()fxMaÎ，2()gxMaÎ，则12()()fxgxMaa××ÎB.若1()fxMaÎ，2()gxMaÎ，且()0gx¹，则12()()fxMgxaaÎC.若1()fxMaÎ，2()gxMaÎ，则12()()fxgxMaa++ÎD.若1()fxMaÎ，2()gxMaÎ，且12aa>，则12()()fxgxMaa--Î二、填空题（本大题共7小题，共0分）11．（2009浙江理11）设等比数列{}na的公比12q=，前n项和为nS，则44Sa=.12．（2009浙江理12）若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是3cm.第4页|共6页13．（2009浙江理13）若实数,xy满足不等式组2,24,0,xyxyxy+³ìï-£íï-³î则23xy+的最小值是14．（2009浙江理14）某地区居民生活用电分为高峰和低谷两个时间段进行分时计价.该地区的电网销售电价表如下：若某家庭5月份的高峰时间段用电量为200千瓦时，低谷时间段用电量为100千瓦时，则按这种计费方式该家庭本月应付的电费为元（用数字作答）.15．（2009浙江理15）观察下列等式：1535522CC+=-，1597399922CCC++=+，159131151313131322CCCC+++=-，1591317157171717171722CCCCC++++=+，………由以上等式推测到一个一般的结论：对于*nNÎ，1594141414141nnnnnCCCC+++++++++=L.16．（2009浙江理16）甲、乙、丙3人站到共有7级的台阶上，若每级台阶最多站2人，同一级台阶上的人不区分站的位置，则不同的站法种数是（用数字作答）.17．（2009浙江理17）如图，在长方形ABCD中，2AB=，1BC=，E为DC的中点，F为线段EC（端点除外）上一动点.现将AFDD沿AF折起，使平面ABD^平面ABC.在平面ABD第5页|共6页内过点D作DKAB^，K为垂足.设AKt=，则t的取值范围是.三、解答题（本大题共5小题，共0分）18．（2009浙江理18）在ABCD中，角,,ABC所对的边分别为,,abc，且满足25cos25A=，3ABAC×=uuuruuur.（I）求ABCD的面积；（II）若6bc+=，求a的值。19．（2009浙江理19）在1,2,3,,9L这9个自然数中，任取3个数.（I）求这3个数中恰有1个是偶数的概率；（II）设x为这3个数中两数相邻的组数（例如：若取出的数为1,2,3，则有两组相邻的数1,2和2,3，此时x的值是2）.求随机变量x的分布列及其数学期望Ex.20．（2009浙江理20）如图，平面PAC^平面ABC，ABCD是以AC为斜边的等腰直角三角形，,,EFO分别为PA，PB，AC的中点，16AC=，10PAPC==.（I）设G是OC的中点，证明：//FG平面BOE；（II）证明：在ABOD内存在一点M，使FM^平面BOE，并求点M到OA，OB的距离.第6页|共6页21．（2009浙江理21）已知椭圆1C：22221(0)yxabab+=>>的右顶点为(1,0)A，过1C的焦点且垂直长轴的弦长为1。（I）求椭圆1C的方程；（II）设点P在抛物线2C：2()yxhh=+ÎR上，2C在点P处的切线与1C交于点,MN当线段AP的中点与MN的中点的横坐标相等时，求h的最小值。22．（2009浙江理22）已知函数322()(1)52fxxkkxx=--++-，22()1gxkxkx=++，其中kÎR.（I）设函数()()()pxfxgx=+.若()px在区间(0,3)上不单调，求k的取值范围；（II）设函数(),0,()(),0.gxxqxfxx³ì=í<î是否存在k，对任意给定的非零实数1x，存在惟一的非零实数2x（21xx¹），使得21()()qxqx¢¢=成立？若存在，求k的值；若不存在，请说明理由.