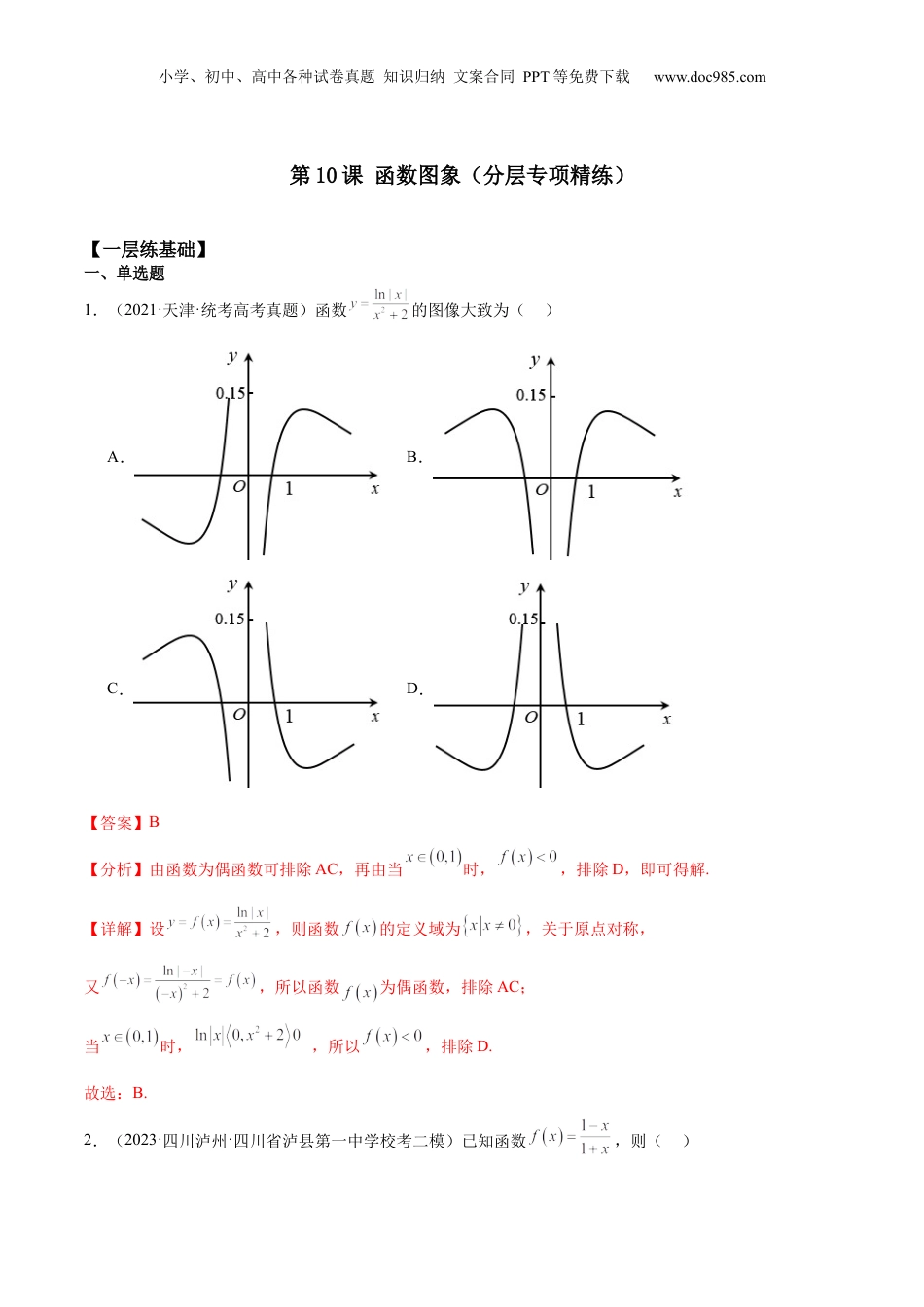
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第10课函数图象（分层专项精练）【一层练基础】一、单选题1．（2021·天津·统考高考真题）函数的图像大致为（）A．B．C．D．【答案】B【分析】由函数为偶函数可排除AC，再由当时，，排除D，即可得解.【详解】设，则函数的定义域为，关于原点对称，又，所以函数为偶函数，排除AC；当时，，所以，排除D.故选：B.2．（2023·四川泸州·四川省泸县第一中学校考二模）已知函数，则（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．在上单调递增B．的图象关于点对称C．为奇函数D．的图象关于直线对称【答案】D【分析】把化简成，进而得到是由先向左平移一个单位，再向下平移一个单位得到的，然后根据的图象画出的图象，即可判断选项【详解】化简得，的可以看作是函数先向左平移一个单位，再向下平移一个单位得到，先画出的图象，再进行平移画出的图象，明显可见，对于原函数，为奇函数，关于点对称，且在和上为单调减函数，所以，经过平移后变成的在上单调递减，关于对称，非奇函数也非偶函数，图象关于直线对称，所以，D正确；A、B、C错误.故选：D3．（2022秋·黑龙江齐齐哈尔·高一齐齐哈尔市第一中学校校考期中）如图所示，点从点出发，按逆时针方向沿边长为的正三角形运动一周，为△的中心，设点走过的路程为，△的面积为（当、、三点共线时，记面积为0），则函数的图象大致为（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．【答案】A【详解】当时,，为一次递增函数,去掉B；当(BC中点)时为一次递减函数，去掉C,D；所以选A.点睛：(1)运用函数性质研究函数图像时，先要正确理解和把握函数相关性质本身的含义及其应用方向.(2)在运用函数性质特别是奇偶性、周期、对称性、单调性、最值、零点时，要注意用好其与条件的相互关系，结合特征进行等价转化研究.如奇偶性可实现自变量正负转化，周期可实现自变量大小转化，单调性可实现去，即将函数值的大小转化自变量大小关系4．（2023·广西柳州·统考模拟预测）已知函数，，若函数在上的大致图象如图所示，则的解析式可能是（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．【答案】D【分析】根据图象判断函数的奇偶性，结合特殊值，可得答案.【详解】易知为偶函数，由，则为奇函数，由图象可知，该函数是奇函数，因为是偶函数，是奇函数，所以是非奇非偶函数，A，B不符合题意.因为当时，无意义，所以C不符合题意.故选：D.二、多选题5．（2023·全国·高三专题练习）关于函数，下列描述正确的有（）A．在区间上单调递增B．的图象关于直线对称C．若则D．有且仅有两个零点【答案】ABD【分析】作出函数的图象，由图象观察性质判断各选项．【详解】根据图象变换作出函数的图象（，作出的图象，再作出其关于轴对称的图象，然后向右平移2个单位，最后把轴下方的部分关于轴翻折上去即可得），如图，由图象知在是单调递增，A正确，函数图象关于直线对称，B正确；，直线与函数图象相交可能是4个交点，如图，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com如果最左边两个交点横坐标分别是，则不成立，C错误，与轴仅有两个公共点，即函数仅有两个零点，D正确．故选：ABD．6．（2021·全国·高三专题练习）如图所示的函数图象，对应的函数解析式不可能是（）A．B．C．D．【答案】ABC【解析】根据图象用特殊值验证、排除可得答案.【详解】由图象可知当时，，而A中函数当时，，B中函数当时，，故A和B不可能；C中函数的定义域是，与图象不符，故C不可能.对于，当时，，当时，，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com当时，，所以D符合，故选：ABC.【点睛】本题考查了函数图象的性质，属于基础题.【二层练综合】一、单选题1．（2023·江西南昌·南昌市八一中学校考三模）函数在上的图像大致为（）A．B．C．D．【答案】B【分析】根据给定的函数，由奇偶性排除两个选项，再取特值即可判断作答.【...