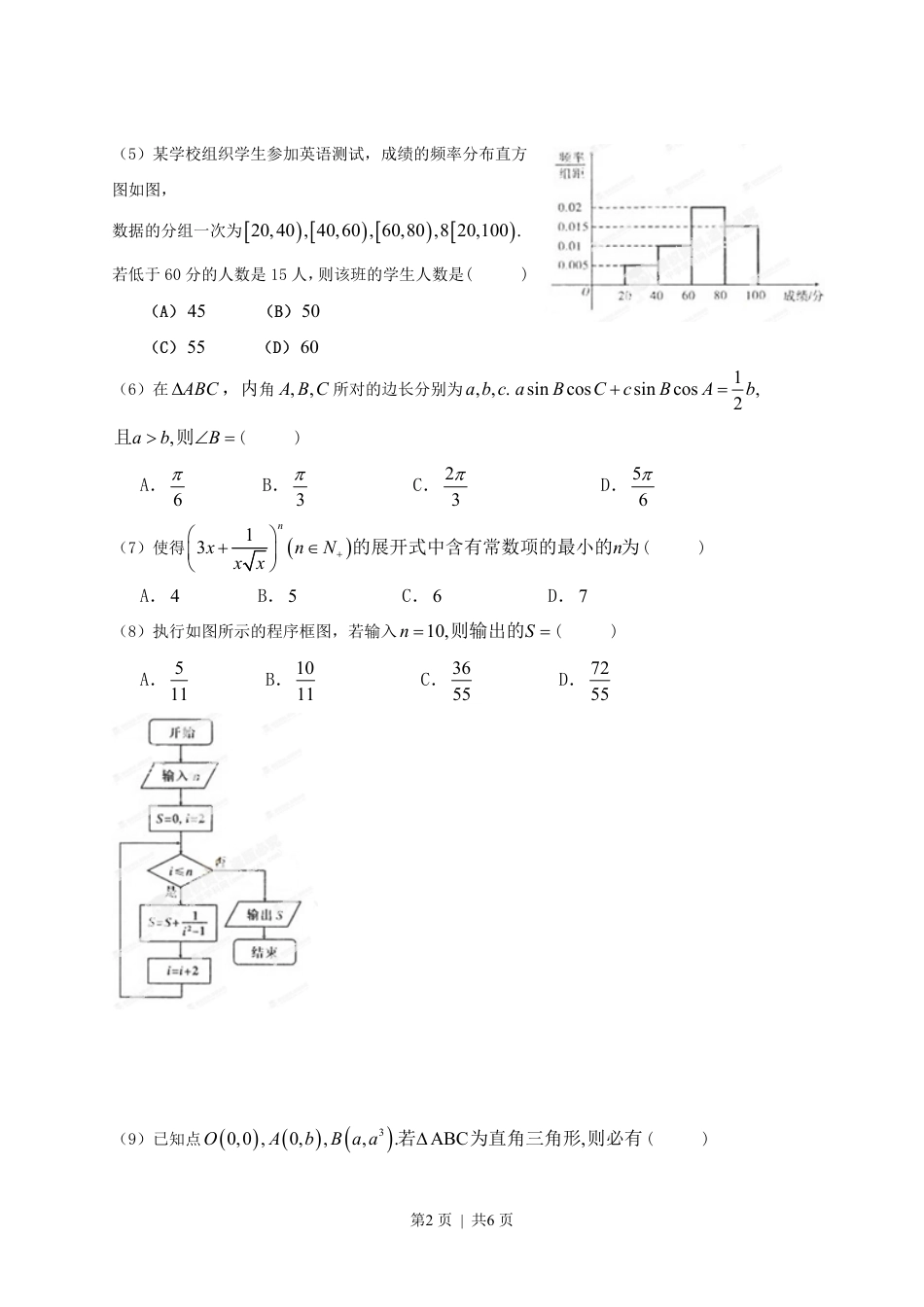
第1页|共6页一、选择题：本大题共12小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.（1）复数的11Zi=-模为()（A）12（B）22（C）2（D）2（2）已知集合4|0log1,|2AxxBxxAB=<<=£=I，则()A．01，B．02，C．1,2D．12，（3）已知点1,3,4,1,ABAB-uuur则与向量同方向的单位向量为()（A）3455æöç÷èø，-（B）4355æöç÷èø，-（C）3455æö-ç÷èø，（D）4355æö-ç÷èø，（4）下面是关于公差0d>的等差数列na的四个命题：1:npa数列是递增数列；2:npna数列是递增数列；3:napnìüíýîþ数列是递增数列；4:3npand+数列是递增数列；其中的真命题为()（A）12,pp（B）34,pp（C）23,pp（D）14,pp第2页|共6页（5）某学校组织学生参加英语测试，成绩的频率分布直方图如图，数据的分组一次为20,40,40,60,60,80,820,100.若低于60分的人数是15人，则该班的学生人数是()（A）45（B）50（C）55（D）60（6）在ABCD，内角,,ABC所对的边长分别为,,.abc1sincossincos,2aBCcBAb+=,abB>Ð=且则()A．6pB．3pC．23pD．56p（7）使得13nxnNnxx+æö+Îç÷èø的展开式中含有常数项的最小的为()A．4B．5C．6D．7（8）执行如图所示的程序框图，若输入10,nS==则输出的()A．511B．1011C．3655D．7255（9）已知点30,0,0,,,.ABC,OAbBaaD若为直角三角形则必有()第3页|共6页A．3ba=B．31baa=+C．3310babaaæö---=ç÷èøD．3310babaa-+--=（10）已知三棱柱1116.34ABCABCOABAC-==的个顶点都在球的球面上若，，,ABAC^112AAO=，则球的半径为()A．3172B．210C．132D．310（11）已知函数222222,228.fxxaxagxxaxa=-++=-+--+设12max,,min,,max,HxfxgxHxfxgxpq==表示,pq中的较大值，min,pq表示,pq中的较小值，记1Hx得最小值为,A2Hx得最小值为B,则AB-=()（A）16（B）16-（C）2216aa--（D）2216aa+-（11）设函数222,2,0,8xeefxxfxxfxfxfxx¢+==>满足则时，()（A）有极大值，无极小值（B）有极小值，无极大值（C）既有极大值又有极小值（D）既无极大值也无极小值第II卷本卷包括必考题和选考题两部分。第13题-第22题为必考题，每个试题考生都必须作答。第22题-第24题为选考题，考生根据要求作答。二、填空题：本大题共4小题，每小题5分.（13）某几何体的三视图如图所示，则该几何体的体积是.第4页|共6页（14）已知等比数列13nnnaSanaa是递增数列,是的前项和.若，是方程26540xxS-+==的两个根，则.（15）已知椭圆2222:1(0)xyCabab+=>>的左焦点为,FC与过原点的直线相交于,AB两点，4,.10,6,cosABF,5AFBFABAFCe==Ð=连接若则的离心率=.（16）为了考察某校各班参加课外书法小组的人数，在全校随机抽取5个班级，把每个班级参加该小组的认为作为样本数据.已知样本平均数为7，样本方差为4，且样本数据互相不相同，则样本数据中的最大值为.三、解答题：解答应写出文字说明、证明过程或演算步骤.17．（本小题满分12分）设向量3sin,sin,cos,sinx,0,.2axxbxxpéù==Îêúëû（I）若.abx=求的值；（II）设函数,.fxabfx=g求的最大值18．（本小题满分12分）如图，.ABPAC是圆的直径，垂直圆所在的平面，是圆上的点（I）求证：PACPBC^平面平面；（II）2.ABACPACPBA===--若，1，1，求证：二面角的余弦值第5页|共6页19．（本小题满分12分）现有10道题，其中6道甲类题，4道乙类题，张同学从中任取3道题解答.（I）求张同学至少取到1道乙类题的概率；（II）已知所取的3道题中有2道甲类题，1道乙类题.设张同学答对甲类题的概率都是35，答对每道乙类题的概率都是45，且各题答对与否相互独立.用X表示张同学答对题的个数，求X的分布列和数学期望.20．（本小题满分12分）如图，抛物线2212002:4,:20.,CxyCxpypMxyC==->点在抛物线上，1MC过作0,,.12ABMOABOx=-的切线，切点为为原点时，重合于当时，1-.2MA切线的斜率为（I）P求的值；（II）2MCABN当在上运动时，求线段中点的轨迹方程,,.A...