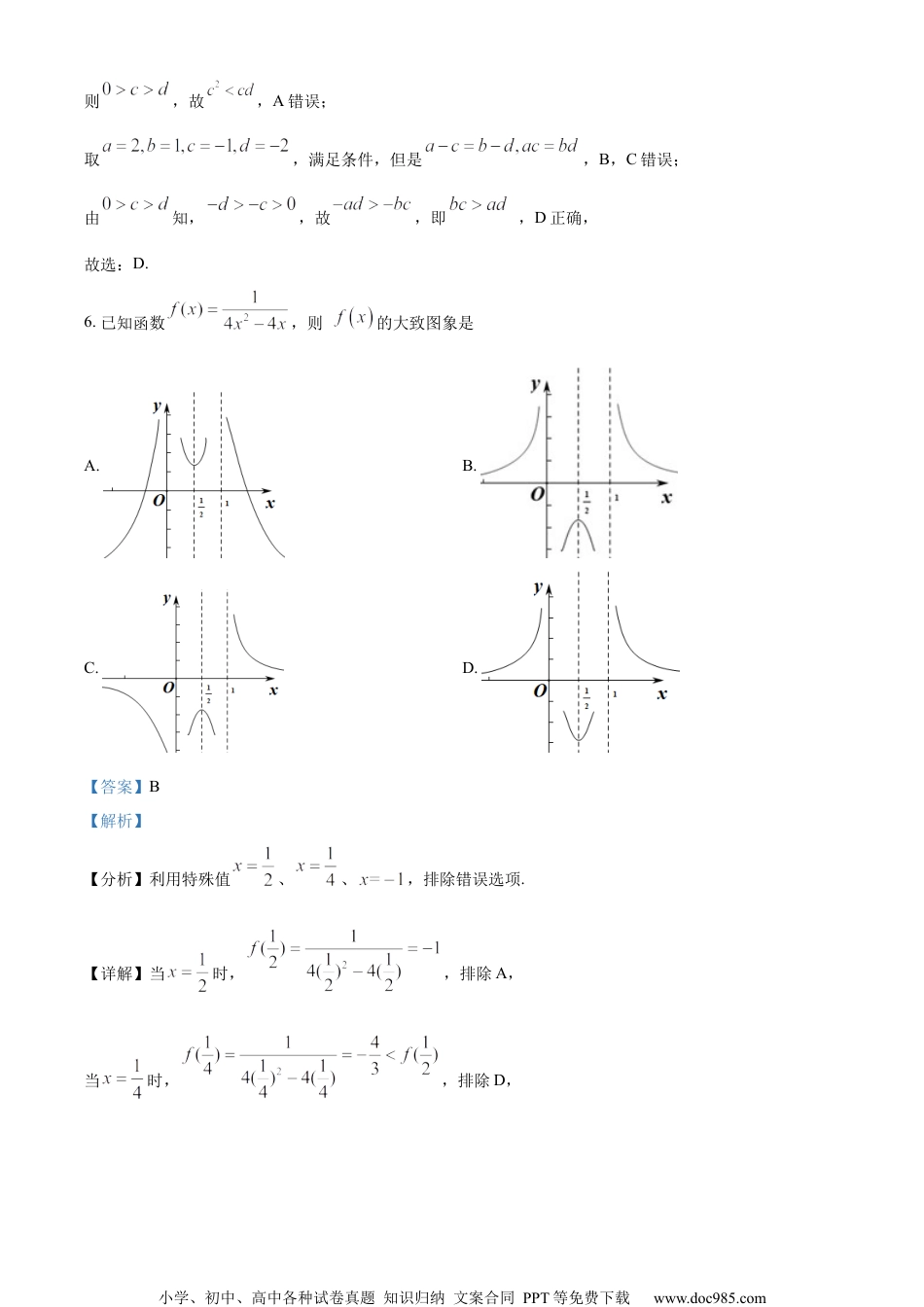
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2022-2023学年南京市第一学期六校联合体期中联合调研高一数学一､选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合，，则()A.B.C.D.【答案】C【解析】【分析】确定集合A中元素，根据集合的交集运算即可求得答案.【详解】由题意得集合，，故，故选:C.2.命题“，”的否定是()A.，B.，C.，D.，【答案】B【解析】【分析】根据含有一个量词的命题的否定，即可确定答案.【详解】命题“，”为特称命题，其否定为全称命题：，，故选：B.3.函数的定义域为()小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA.B.C.D.【答案】B【解析】【分析】根据函数的解析式有意义，列出不等式组，即可求解.【详解】由题意，函数有意义，则满足，解得且，所以函数的定义域为.故选：B4.设，，则=()A.B.C.D.【答案】D【解析】【分析】根据对数的运算，化简为，即可得答案.【详解】由题意知，，则，故选：D5.已知均为实数，且，则下列结论正确的是()A.B.C.D.【答案】D【解析】【分析】根据不等式的性质可判断A,D;举反例可判断B,C,即得答案.【详解】由题意均为实数，且，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com则，故，A错误；取，满足条件，但是，B，C错误；由知，，故，即，D正确，故选：D.6.已知函数，则的大致图象是A.B.C.D.【答案】B【解析】【分析】利用特殊值、、，排除错误选项.【详解】当时，，排除A，当时，，排除D，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com当时，，排除C，故选B.【点睛】从函数解析式结合选项，发现零点、单调性、奇偶性、过特殊点等性质，是求解函数图象问题的常见方法.7.已知关于的不等式的解集是，则不等式的解集是()A.B.C.D.【答案】C【解析】【分析】根据不等式的解集确定是方程的两个实数根，且，进而得，化简为，即可求得答案.【详解】由题意关于的不等式的解集是，可知是方程的两个实数根，且，则，则，故即，即或，即不等式的解集是，故选：C.8.已知是奇函数，且在上是增函数，又，则的解集为()A.B.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC.D.【答案】A【解析】【分析】根据函数的奇偶性以及在上的单调性确定函数值的正负情况，结合可得相应不等式组，即可求得答案.【详解】因为定义在R上的奇函数在上单调递增，且，所以在上也是单调递增，且，所以当时，，当时，，所以由可得或,即或，解得或，即的解集为，故选：A.【点睛】本题考查了函数的奇偶性以及单调性的综合应用，考查抽象不等式的解法，解答时要明确函数的对称性质，进而判断函数值的正负情况，解答的关键时根据不等式结合函数值情况得到相应不等式组，求得结果.二､选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.9.下列各组函数中是同一个函数的是()A.与B.与小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC.与D.与【答案】AC【解析】【分析】根据函数的定义,只需对应关系和定义域一致,即可判断为同一个函数.【详解】关于选项A,因为对应关系和定义域一致,所以A是同一个函数;关于选项B,因为的定义域为,定义域为R,定义域不一致,所以B不是同一个函数;关于选项C,因为对应关系和定义域一致,所以C是同一个函数;关于选项D,因为的定义域为,可得,定义域为,定义域不一致,所以D不是同一个函数.故选:AC10.下列命题中正确的是()A.若，则B.若且，则C.D.【答案】ABD【解析】【分析】将时，化为，利用均值不等式可判断A;利用，利用均值不等式可判断B；将化为，利用均值不等式可判断C；利用小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com，结合均值不等式判断D.【详解】当时，，则，当且仅当时取等号，故A正确；若且，则，当或时取等号，B正确；由，故，当时，不成立，故等号取不到，C错误；，当且仅当时取等号，...