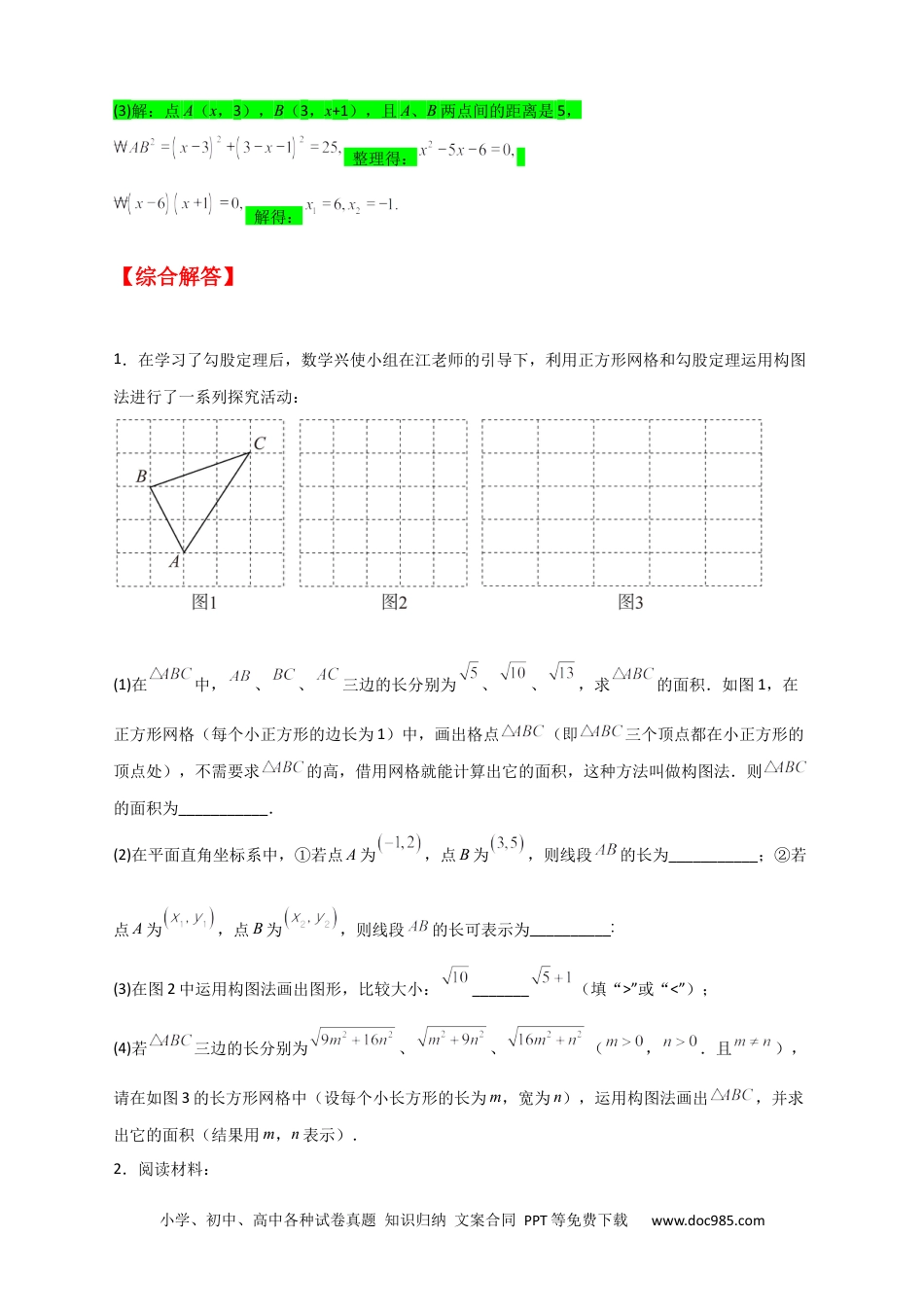
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题14已知两点坐标求两点距离【例题讲解】阅读材料：两点间的距离公式：如果直角坐标系内有两点A（x1，y1）、B（x2，y2），那么A、B两点的距离AB＝．则AB2＝（x1﹣x2）2+（y1﹣y2）2．例如：若点A（4，1），B（2，3），则AB＝根据上面材料完成下列各题：(1)若点A（﹣2，3），B（1，﹣3），则A、B两点间的距离是．(2)若点A（﹣2，3），点B在坐标轴上，且A、B两点间的距离是5，求B点坐标．(3)若点A（x，3），B（3，x+1），且A、B两点间的距离是5，求x的值．(1)解：点A（﹣2，3），B（1，﹣3），则A、B两点间的距离是：故答案为：(2)解：点B在坐标轴上，设或当时，点A（﹣2，3），且A、B两点间的距离是5，或或当时，点A（﹣2，3），且A、B两点间的距离是5，或解得：或小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com(3)解：点A（x，3），B（3，x+1），且A、B两点间的距离是5，整理得：解得：【综合解答】1．在学习了勾股定理后，数学兴使小组在江老师的引导下，利用正方形网格和勾股定理运用构图法进行了一系列探究活动：(1)在中，、、三边的长分别为、、，求的面积．如图1，在正方形网格（每个小正方形的边长为1）中，画出格点（即三个顶点都在小正方形的顶点处），不需要求的高，借用网格就能计算出它的面积，这种方法叫做构图法．则的面积为___________．(2)在平面直角坐标系中，①若点A为，点B为，则线段的长为___________；②若点A为，点B为，则线段的长可表示为__________∶(3)在图2中运用构图法画出图形，比较大小：_______（填“>”或“<”）；(4)若三边的长分别为、、（，．且），请在如图3的长方形网格中（设每个小长方形的长为m，宽为n），运用构图法画出，并求出它的面积（结果用m，n表示）．2．阅读材料：小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com两点间的距离公式：如果直角坐标系内有两点A（x1，y1）、B（x2，y2），那么A、B两点的距离AB＝．则AB2＝（x1﹣x2）2+（y1﹣y2）2．例如：若点A（4，1），B（2，3），则AB＝根据上面材料完成下列各题：(1)若点A（﹣2，3），B（1，﹣3），则A、B两点间的距离是．(2)若点A（﹣2，3），点B在坐标轴上，且A、B两点间的距离是5，求B点坐标．(3)若点A（x，3），B（3，x+1），且A、B两点间的距离是5，求x的值．3．（一）问题提出（1）平面直角坐标系中，如果A、B是x轴上的点，他们对应的横坐标分别是xA，xB，C、D是y轴上的两点，它们对应的纵坐标分别是yC，yD，那么A、B两点间的距离，C、D两点间的距离分别是多少？（2）平面直角坐标系中任意一点P(x，y)到原点的距离是多少？（3）已知平面上的两点P1(x1，y1)，P2(x2，y2)，如何求P1，P2的距离|P1P2|（二）问题探究（1）求平面直角坐标系中x轴上的两点E(5，0)、F(-2，0)之间的距离，可以借助绝对值表示|EF|=|5-（-2）|=7，对于y轴上两点，M(0，-3)、N(0，5)之间的距离|MN|=|3-5|=2．结论：在平面直角坐标系中，如果A、B是x轴上两点，它们对应的横坐标分别是xA，xB，则A、B两点间的距离|AB|＝；C、D是y轴上的两点，它们对应的纵坐标分别是yC，yD，那么C、D两点间的距离|CD|＝：（2）如图1：平面直角坐标系中任意一点B(3，4)，过B向x轴上作垂线，垂足为M，由勾股定理得|OB|＝；结论：平面直角坐标系中任意一点P(x，y)到原点的距离|OP|＝；（3）如图2，要求AB或DE的长度，可以转化为求RtABC或RtDEF的斜边长．例如：从坐标系中发现：D(-7，5)，E(4，-3)，所|以|DF|=|5-（-3）|=8，|EF|=|4-（-7）|=11，所以由勾股定理得：|DE|=．在图2中请用上面的方法求线段AB的长：AB＝；在图3中：设P1(x1，y1)，P2(x2，y2)，试用x1，x2，y1，y2表示：|P1C|＝，|P2C|＝，|P1P2|＝．（三）拓展应用试用以上所得结论解决如下问题：已知A(0，1)，B(4，3)．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（1）直线AB与x轴交于点D，求线段BD的长．（2）C为坐标轴上的点，且使得三角形ABC是以AB为底边的等腰三角形，则C点的坐标为（不必写解...