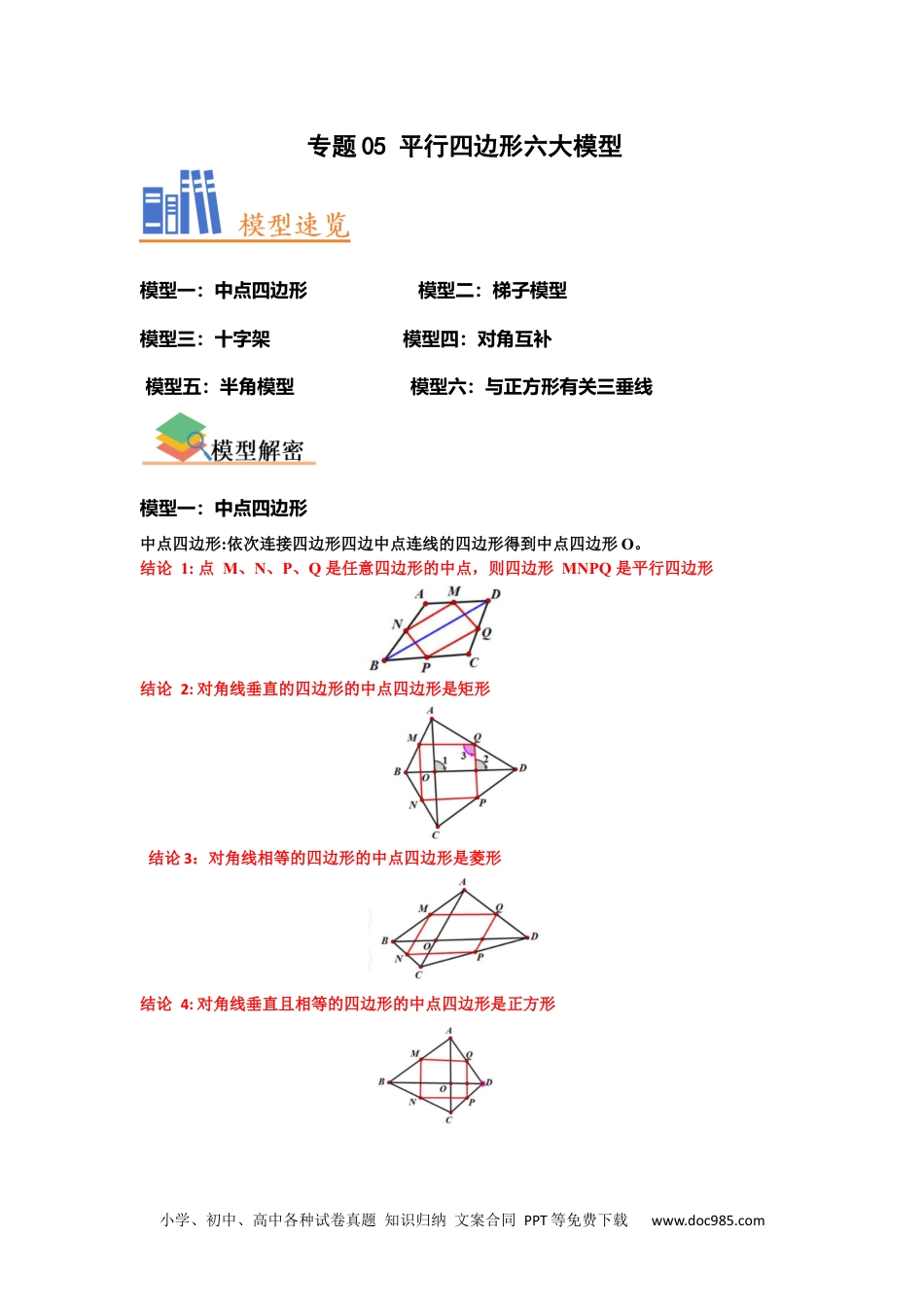
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题05平行四边形六大模型模型一：中点四边形模型二：梯子模型模型三：十字架模型四：对角互补模型五：半角模型模型六：与正方形有关三垂线模型一：中点四边形中点四边形:依次连接四边形四边中点连线的四边形得到中点四边形O。结论1:点M、N、P、Q是任意四边形的中点，则四边形MNPQ是平行四边形结论2:对角线垂直的四边形的中点四边形是矩形结论3：对角线相等的四边形的中点四边形是菱形结论4:对角线垂直且相等的四边形的中点四边形是正方形小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【典例1】（2024•长沙模拟）如图，E、F、G、H分别是四边形ABCD四条边的中点，则四边形EFGH一定是（）A．平行四边形B．矩形C．菱形D．正方形【答案】A【解答】解：如图，连接AC， E、F、G、H分别是四边形ABCD边的中点，∴HG∥AC，HG＝AC，EF∥AC，EF＝AC；∴EF＝HG且EF∥HG；∴四边形EFGH是平行四边形．故选：A．【变式1-1】（2023•阳春市二模）若顺次连接四边形ABCD各边的中点所得的四边形是菱形，则四边形ABCD的两条对角线AC，BD一定是（）A．互相平分B．互相平分且相等C．互相垂直D．相等【答案】D【解答】解： E，F，G，H分别是边AD，DC，CB，AB的中点，∴EH＝AC，EH∥AC，FG＝AC，FG∥AC，EF＝BD，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com∴EH∥FG，EF＝FG，∴四边形EFGH是平行四边形，假设AC＝BD， EH＝AC，EF＝BD，则EF＝EH，∴平行四边形EFGH是菱形，即只有具备AC＝BD即可推出四边形是菱形，故选：D．【变式1-2】（2023•铜川一模）如图，AC、BD是四边形ABCD的两条对角线，顺次连接四边形ABCD各边中点得到四边形EFGH，要使四边形EFGH为矩形，应添加的条件是（）A．AC⊥BDB．AB＝CDC．AB∥CDD．AC＝BD【答案】A【解答】解： E、F、G、H分别为AB、BC、CD、AD的中点，∴EF＝AC，EF∥AC，GH＝AC，GH∥AC，EH∥BD，∴EF＝GH，EF∥GH，∴四边形EFGH为平行四边形，当AC⊥BD时，EF⊥EH，则四边形EFGH为矩形，故选：A．【变式1-3】（2023春•宿豫区期中）顺次连接对角线相等且垂直的四边形四边中点所得的四边形一定是（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．平行四边形B．矩形C．菱形D．正方形【答案】D【解答】解： E、F、G、H分别是AB、BC、CD、AD的中点，∴EH∥FG∥BD，EF∥AC∥HG，EF＝AC，FG＝BD，∴四边形EFGH是平行四边形， AC⊥BD，AC＝BD，∴EF⊥FG，FE＝FG，∴四边形EFGH是正方形，故选：D．模型二：梯子模型如下图，一根长度一定的梯子斜靠在竖直墙面上,当梯子底端滑动时,探究梯子上某点(如中点)或梯子构成图形上的点的轨迹模型(图2),就是所谓的梯子模型。[考查方向]已知一条线段的两个端点在坐标轴上滑动,求线段最值问题。模型一:如图所示,线段AC的两个端点在坐标轴上滑动，LACB=ZAOC=90°AC的中点为P,连接OP、BP、OB,则当O、P、B三点共线时,此时线段OB最大值。小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com即已知RtAACB中AC、BC的长,就可求出梯子模型中OB的最值模型二:如图所示,矩形ABCD的顶点A、B分别在边OM、ON上,当点A在边OM上运动时,点B随之在ON上运动，且运动的过程中矩形ABCD形状保持不变，AB的中点为P,连接OP、PD、OD,则当O、P、D三点共线时,此时线段OD取最大值【典例2】如图，∠MON＝90°，矩形ABCD的顶点A、B分别在边OM、ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB＝6，BC＝2．运动过程中点D到点O的最大距离是3+．【答案】见试题解答内容【解答】解：如图：取线段AB的中点E，连接OE，DE，OD，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com AB＝6，点E是AB的中点，∠AOB＝90°，∴AE＝BE＝3＝OE， 四边形ABCD是矩形，∴AD＝BC＝2，∠DAB＝90°，∴DE＝＝， OD≤OE+DE，∴当点D，点E，点O共线时，OD的长度最大．∴点D到点O的最大距离＝OE+DE＝3+，故答案为：3+．【变式2-1】如图，在Rt△...