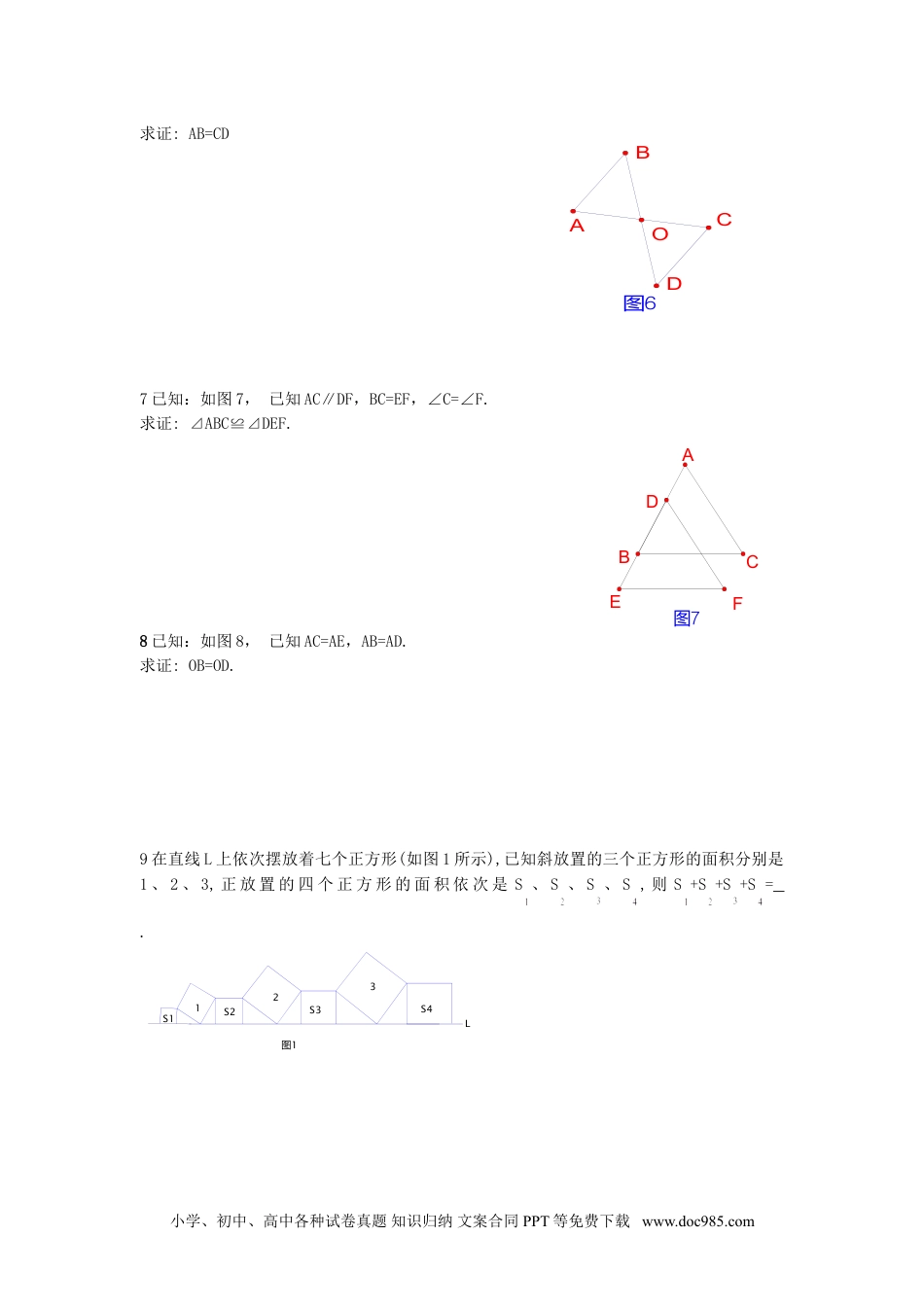
图1CABFDE勾股定理习题1已知：如图1，点A、D、B、E在同一条直线上，AD=BE,AC∥DF,BC∥EF.求证:AC=DF.2已知：如图2，BE⊥AC,DF⊥AC,垂足分别是E、F,O是BD的中点.求证:BE=DF.3已知：如图3，AB=DE,BC=EF,AF=CD.求证:AB∥DE,BC∥EF.4已知：如图4，AB=AD,AC=AE,∠BAD=∠CAE.求证:.∠B=∠D.5已知：如图5，AD=AE,点D、E在BC上，BD=CE,∠ADE=∠AED.求证:⊿ABE≌⊿ACD6已知：如图6，已知AC、BD相交于点O，AB∥CD,OA=OC.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com图5CDAEB求证:AB=CD7已知：如图7，已知AC∥DF，BC=EF，∠C=∠F.求证:⊿ABC≌⊿DEF.8已知：如图8，已知AC=AE，AB=AD.求证:OB=OD.9在直线L上依次摆放着七个正方形(如图1所示),已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S、S、S、S,则S+S+S+S=.S4S3S2S1图1L321小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com图6OABDC图7ABCFED10张老师在一次“探究性学习”课中，设计了如下表：n2345…a…b46810…c…（1）请你分别观察a、b、c与n（n＞1）之间的关系，并分别用含n的代数式表示a、b、c：a=，b=，c=；（2）猜想以a、b、c为边的三角形是否为直角三角形，并验证你的猜想.11分析：这是一道结论开放题，据题意经过分析，符合要求的点C有多个，如图2所示，，，，，，都是符合要求的点.参考答案1思路分析：要证明AC=DF，则需要证明⊿ABC≌⊿DEF.在⊿ABC和⊿DEF中，由AC∥DF可小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com得∠CAB=∠FDE,由BC∥EF可得∠CBA=∠FED,现已证两三角形的两组对应角相等，所以考虑夹边，用ASA，证明⊿ABC≌⊿DEF．由已知AD=BE可得：AD+DB=BE+DB,即AB=DE，命题得证．2思路分析：要证明BE=DF，则需要证明⊿BOE≌⊿DOF.在⊿BOE和⊿DOF中，由BE⊥AC,DF⊥AC可得∠BEO=∠DFO=90°,∠BOE=∠DOF,现已证两三角形的两组对应角相等，所以考虑其中一组对应角的对边，用AAS，证明⊿BOE≌⊿DOF．由已知O是BD的中点可得：OB=OD，条件已具备，命题得证．3思路分析：要证明AB∥DE,BC∥EF，则需要证明∠A=∠D,∠BCA=∠EFD,由此只需要证明⊿ABC≌⊿DEF.在⊿ABC和⊿DEF中，已知AB=DE,BC=EF,即两三角形的两组对应边相等，因此，只需证明边AC=DF，用SSS证明⊿ABC≌⊿DEF．由已知AF=CD，根据等式性质得：AF+CF=CD+CF,即AC=DF，命题得证．4思路分析：要证明∠B=∠D，只需要证明⊿ABC≌⊿ADE.在⊿ABC和⊿ADE中，已知AB=AD,AC=AE,即两三角形的两组对应边相等，因此，只需证明两条已知边的夹角相等，用SAS证明⊿ABC≌⊿ADE．由已知∠BAD=∠CAE，根据等式性质得：∠BAD+∠DAC=∠CAE+∠DAC，即∠BAC=∠DAE，命题得证．5思路分析：要证明⊿ABE≌⊿ACD，在⊿ABE和⊿ACD中，已知AD=AE,∠ADE=∠AED即相邻的一角一边对应相等，因此，只需证明∠ADE与∠AED的另一邻边相等即可，用SAS证明⊿ABE≌⊿ACD．由已知BD=CE可得：BD+DE=CE+DE,即BE=CD，命题得证．6思路分析：要证明AB=CD，则需要证明⊿ABO≌⊿CDO.在⊿ABO和⊿CDO中，已知OA=OC,∠AOB=∠COD即相邻的一角一边对应相等，因此，只需证明OA与OC的另一邻角相等即可，用ASA证明⊿ABO≌⊿CDO．由已知AB∥CD可得：∠A=∠C，命题得证．7思路分析：要证明⊿ABC≌⊿DEF,在⊿ABC和⊿DEF中，已知BC=EF,∠C=∠F,即相邻的一角一边对应相等，因此，只需证明已知边的对角相等（∠A=∠EDF）即可，从而用AAS证明⊿ABC≌⊿DEF．由已知AC∥DF可得：∠A=∠EDF，命题得证．8思路分析：要证明OB=OD，则需要证明⊿BOE≌⊿DOC，已知一边和它的对角相等，即由AC=AE，AB=AD可得BE=DC，对顶角∠BOE=∠DOC，从而只要证明另一组角相等（∠B=∠D）即可．要证明∠B=∠D，只需要证明⊿ABC≌⊿ADE，因为题中已知AC=AE，AB=AD，∠A是公共角，所以⊿BOE≌⊿DOC，∠B=∠D得证，从而命题得证．9分析:经过观察图形,可以看出正放着正方形面积与斜放置的正方形之间关系为:S+S=1;S+S=2;S+S=3;这样数形结合可把问题解决.解:S代表的面积为S的正方形边长的平方,S代表的面积为S的正方形边长的平方,所以S+S=斜放置的正方形面...