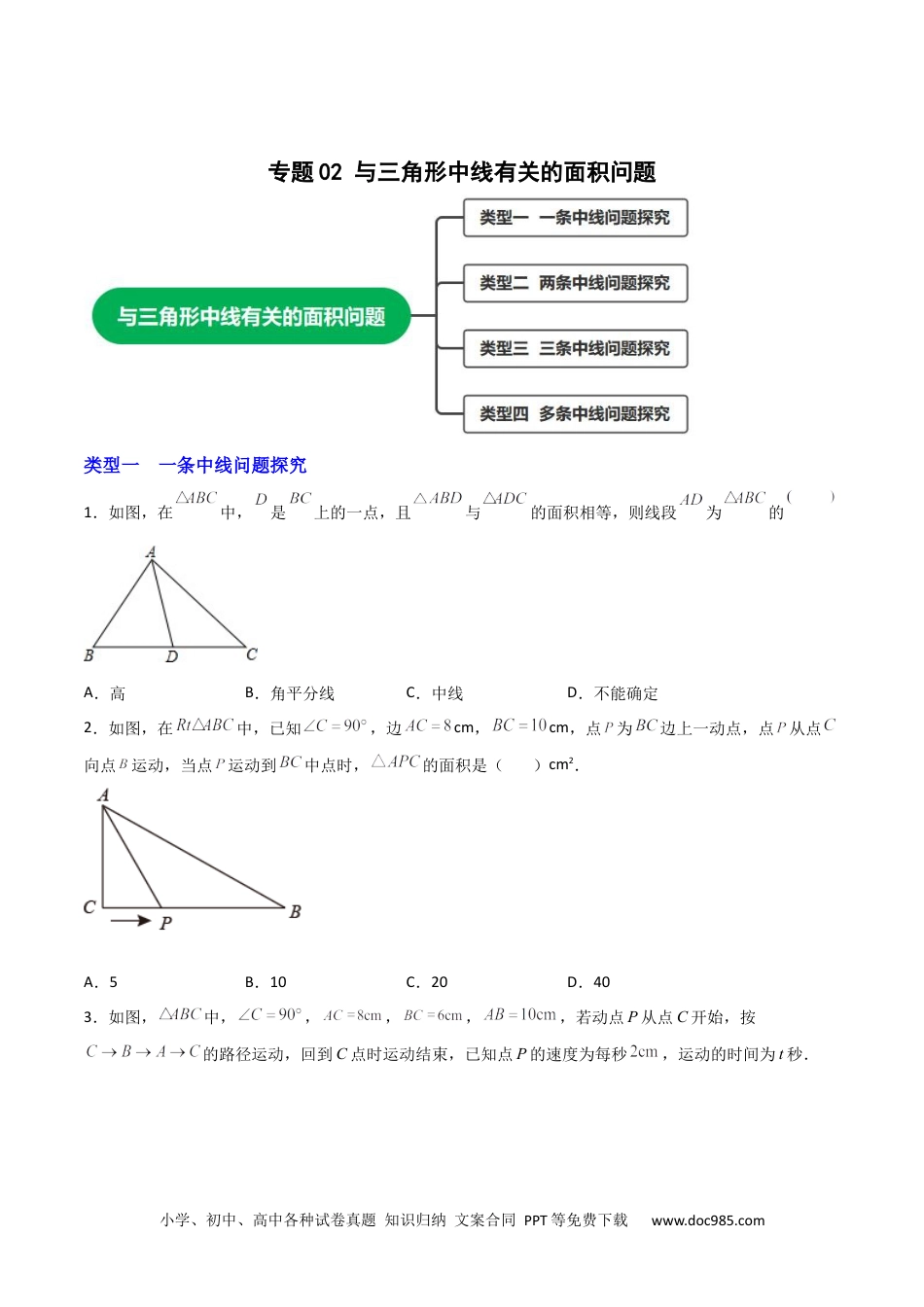
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题02与三角形中线有关的面积问题类型一一条中线问题探究1．如图，在中，是上的一点，且与的面积相等，则线段为的A．高B．角平分线C．中线D．不能确定2．如图，在中，已知，边cm，cm，点为边上一动点，点从点向点运动，当点运动到中点时，的面积是（）cm2．A．5B．10C．20D．403．如图，中，，，，，若动点P从点C开始，按的路径运动，回到C点时运动结束，已知点P的速度为每秒，运动的时间为t秒．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（1）当_____时，把的周长分成相等的两部分？（2）当_____时，把的面积分成相等的两部分？（3）当t为何值时，的面积的6？类型二两条中线问题探究4．如图，已知AD是△ABC的边BC上的中线，CE是△ADC的边AD上的中线，若△ABD的面积为16cm2，则△CDE的面积为（）A．32cm2B．16cm2C．8cm2D．4cm25．如图，在△ABC中，D、E分别是AC、BC边上的一点，AD＝2DC，BE＝EC，若△DBE的面积为1，则△ABC的面积等于（）A．4B．6C．8D．106．如图，△ABC的两条中线AM、BN相交于点O，已知△ABO的面积为4，△BOM的面积为2，则四边形MCNO的面积为（）A．4B．3小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC．4.5D．3.57．如图，△ABC的中线AD、BE相交于点P，四边形与△ABP的面积分别记为S1、S2，则S1与S2的大小关系为（）A．S1＞S2B．S1＝S2C．S1＜S2D．以上都有可能8．如图，在中，是边上的点，是边上的点，且，，若的面积为1，则的面积为（）A．B．C．D．9．如图，△ABC中，D为边BC上的一点，中线BE与线段AD交于点F，且DF＝AD，△ABD的面积为2，则△ADC的面积为___．类型三三条中线问题探究10．如图所示，在△ABC中，D、E、F分别为BC、AD、CE的中点，且S△ABC＝16cm2，则阴影部分（△BEF）的面积等于（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．2cm2B．4cm2C．6cm2D．8cm211．如图，是的中线，点、分别为、的中点，若的面积为，则的面积是______．12．如图，△ABC中，D是BC边上的一点(不与B，C重合)，点E，F是线段AD的三等分点，记△BDF的面积为S1，△ACE的面积为S2，若S1+S2=3，则△ABC的面积为______13．如图，分别是的边上的中点，连接交于点，，的面积为，设的面积为，的面积为，则_______．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com14．如图，已知△ABC，现将边BA延长至点D，使AD=AB，延长AC到点E，使CE=2AC，延长CB至点F，使BF=3BC，分别连接DE，DF，EF，得到△DEF，若△ABC的面积为2，则阴影部分的面积=_______________．15．如图，△ABC的面积是1，AD是△ABC的中线，AF＝FD，CE＝EF，则△DEF的面积为（）A．B．C．D．16．阅读下面资料：小明遇到这样一个问题：如图1，对面积为a的△ABC逐次进行以下操作：分别延长AB、BC、CA至A1、B1、C1，使得A1B2AB，B1C2BC，C1A2CA，顺次连接A1、B1、C1，得到△A1B1C1，记其面积为S1，求S1的值.小明是这样思考和解决这个问题的：如图2，连接A1C、B1A、C1B，因为A1B2AB，B1C2BC，C1A2CA，根据等高两三角形的面积比等于底之比，所以2SABC△2a，由此继续推理，从而解决了这个问题.（1）直接写出S1（用含字母a的式子表示）.请参考小明同学思考问题的方法，解决下列问题：小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（2）如图3，P为△ABC内一点，连接AP、BP、CP并延长分别交边BC、AC、AB于点D、E、F，则把△ABC分成六个小三角形，其中四个小三角形面积已在图上标明，求△ABC的面积.（3）如图4，若点P为△ABC的边AB上的中线CF的中点，求S△APE与S△BPF的比值.类型四多条中线问题探究17．如图，△ABC的面积为1，沿△ABC的中线截取的面积为，沿的中线截取的面积为．按上述方法依次截取的三角形的面积分别为，…，则所截取的三角形的面积之和为______．18．设△ABC的面积为1，如图①将边BC、AC分别2等分，BE1、AD1相交于点O，△AOB的面积记为S1；如图②将边BC...