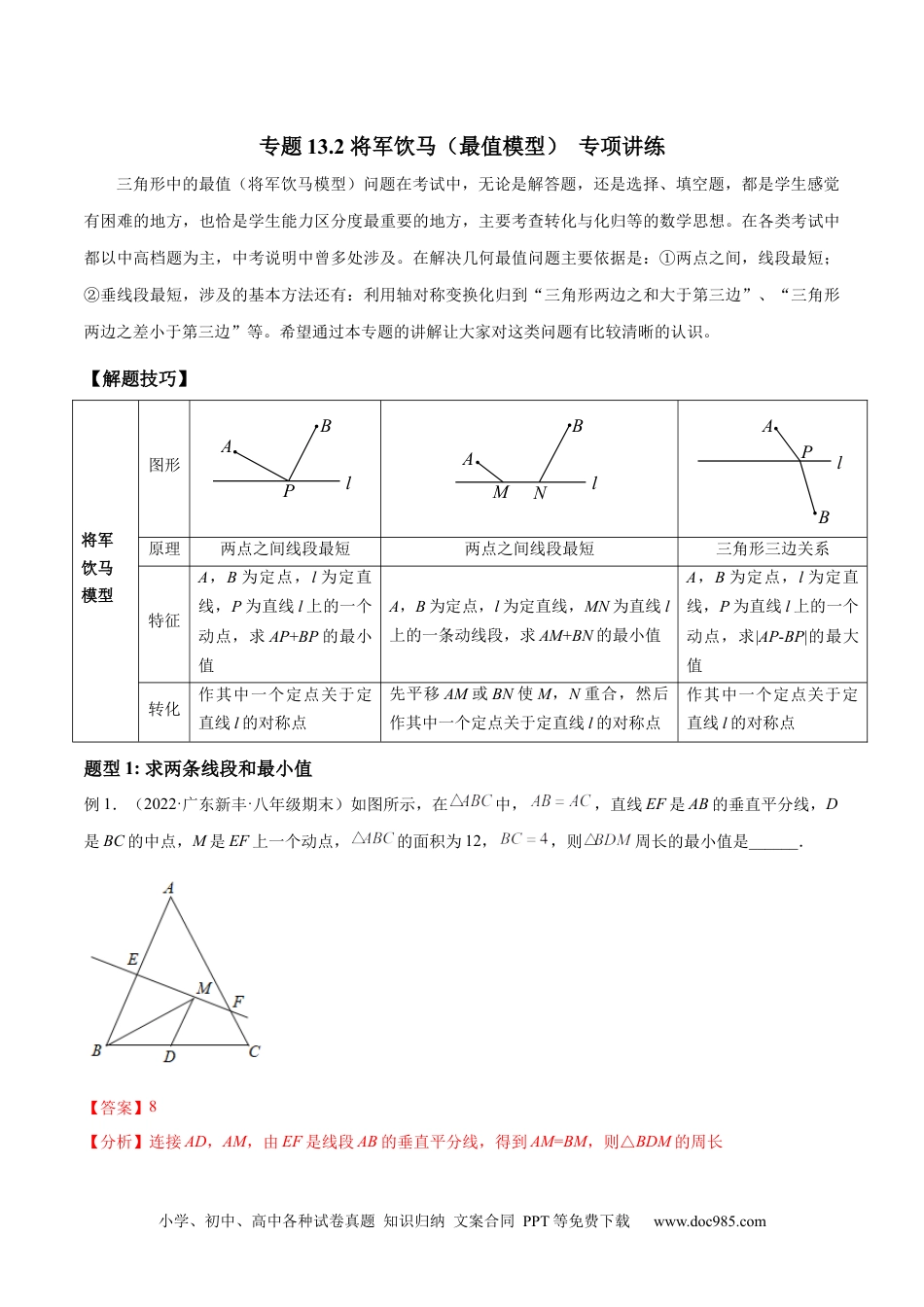
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题13.2将军饮马（最值模型）专项讲练三角形中的最值（将军饮马模型）问题在考试中，无论是解答题，还是选择、填空题，都是学生感觉有困难的地方，也恰是学生能力区分度最重要的地方，主要考查转化与化归等的数学思想。在各类考试中都以中高档题为主，中考说明中曾多处涉及。在解决几何最值问题主要依据是：①两点之间，线段最短；②垂线段最短，涉及的基本方法还有：利用轴对称变换化归到“三角形两边之和大于第三边”、“三角形两边之差小于第三边”等。希望通过本专题的讲解让大家对这类问题有比较清晰的认识。【解题技巧】将军饮马模型图形lPBANMlBAAPBl原理两点之间线段最短两点之间线段最短三角形三边关系特征A，B为定点，l为定直线，P为直线l上的一个动点，求AP+BP的最小值A，B为定点，l为定直线，MN为直线l上的一条动线段，求AM+BN的最小值A，B为定点，l为定直线，P为直线l上的一个动点，求|AP-BP|的最大值转化作其中一个定点关于定直线l的对称点先平移AM或BN使M，N重合，然后作其中一个定点关于定直线l的对称点作其中一个定点关于定直线l的对称点题型1:求两条线段和最小值例1．（2022·广东新丰·八年级期末）如图所示，在中，，直线EF是AB的垂直平分线，D是BC的中点，M是EF上一个动点，的面积为12，，则周长的最小值是______．【答案】8【分析】连接AD，AM，由EF是线段AB的垂直平分线，得到AM=BM，则△BDM的周长小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com=BD+BM+DM=AM+DM+BD，要想△BDM的周长最小，即要使AM+DM的值最小，故当A、M、D三点共线时，AM+DM最小，即为AD，由此再根据三线合一定理求解即可．【详解】解：如图所示，连接AD，AM， EF是线段AB的垂直平分线，∴AM=BM，∴△BDM的周长=BD+BM+DM=AM+DM+BD，∴要想△BDM的周长最小，即要使AM+DM的值最小，∴当A、M、D三点共线时，AM+DM最小，即为AD， AB=AC，D为BC的中点，∴AD⊥BC，，∴，∴AD=6，∴△BDM的周长最小值=AD+BD=8，故答案为：8．【点睛】本题主要考查了线段垂直平分线的性质，三线合一定理，解题的关键在于能够根据题意得到当A、M、D三点共线时，AM+DM最小，即为AD．变式1．（2022·甘肃西峰·八年级期末）如图，在等边△ABC中，E为AC边的中点，AD垂直平分BC，P是AD上的动点．若AD=6，则EP+CP的最小值为_______________．【答案】6【分析】要求EP+CP的最小值，需考虑通过作辅助线转化EP，CP的值，从而找出其最小值求解．【详解】解：作点E关于AD的对称点F，连接CF，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com △ABC是等边三角形，AD是BC边上的中垂线，∴点E关于AD的对应点为点F，∴CF就是EP+CP的最小值． △ABC是等边三角形，E是AC边的中点，∴F是AB的中点，∴CF=AD=6，即EP+CP的最小值为6，故答案为6．【点睛】本题考查等边三角形的性质和轴对称等知识，熟练掌握等边三角形和轴对称的性质是本题的关键．变式2．（2021·湖北洪山·八年级期中）如图，将△ABC沿AD折叠使得顶点C恰好落在AB边上的点M处，D在BC上，点P在线段AD上移动，若AC＝6，CD＝3，BD＝7，则△PMB周长的最小值为___．【答案】18【分析】首先明确要使得△PMB周长最小，即使得PM+PB最小，再根据翻折的性质可知PM=PC，从而可得满足PC+PB最小即可，根据两点之间线段最短确定BC即为最小值，从而求解即可．【详解】解：由翻折的性质可知，AM=AC，PM=PC，∴M点为AB上一个固定点，则BM长度固定， △PMB周长=PM+PB+BM，∴要使得△PMB周长最小，即使得PM+PB最小， PM=PC，∴满足PC+PB最小即可，显然，当P、B、C三点共线时，满足PC+PB最小，如图所示，此时，P点与D点重合，PC+PB=BC，∴△PMB周长最小值即为BC+BM，此时，作DS⊥AB于S点，DT⊥AC延长线于T点，AQ⊥BC延长线于Q点，由题意，AD为∠BAC的角平分线，∴DS=DT， ，，∴，即：，∴，解得：AB=14， AM=AC=6，∴BM=14-6=8，∴△PMB周长最小值为BC+BM=3+7+8=18，故答案为：18．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.d...