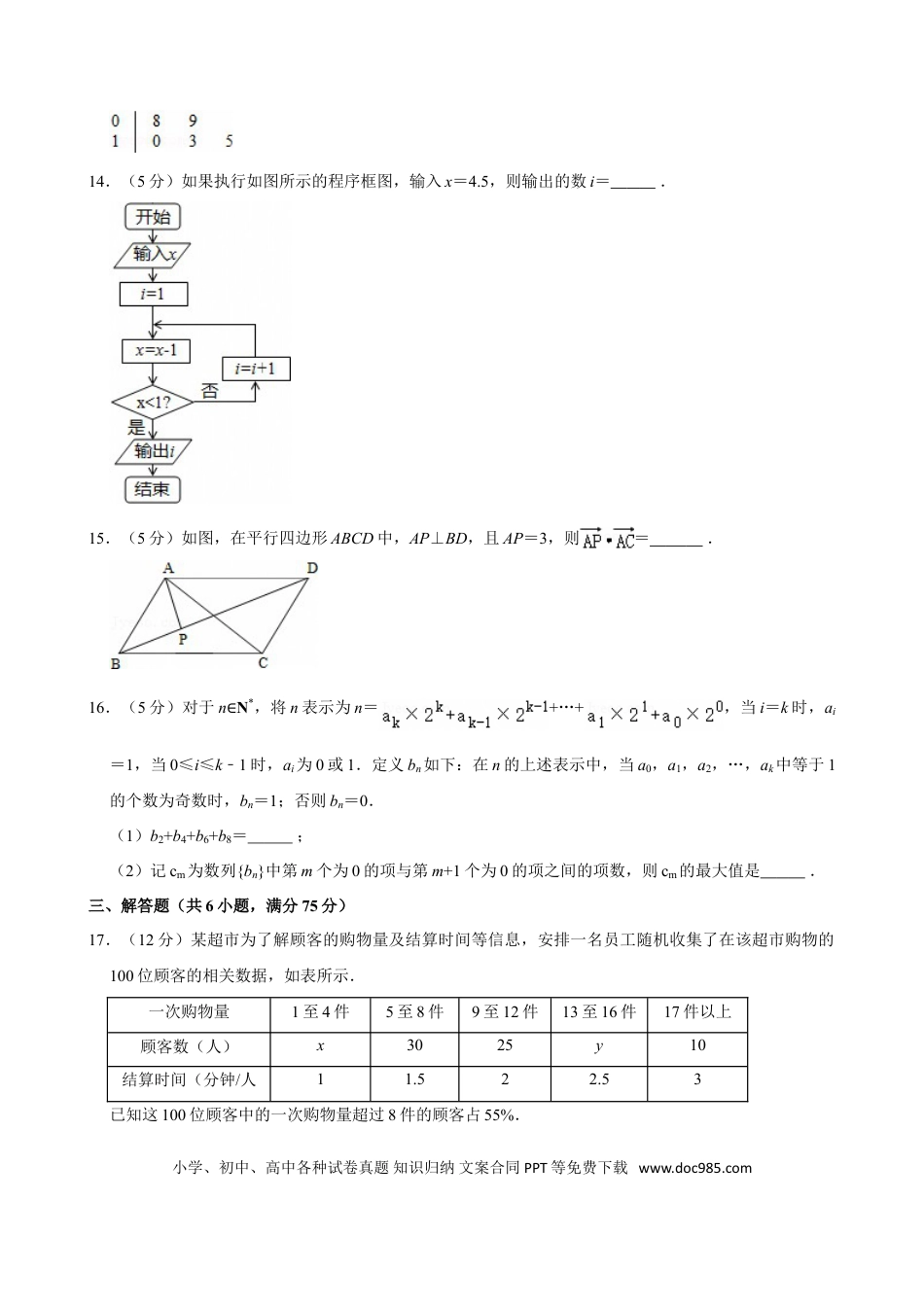
2012年湖南省高考数学试卷（文科）一、选择题（共9小题，每小题5分，满分45分）1．（5分）设集合M＝{﹣1，0，1}，N＝{x|x2＝x}，则M∩N＝（）A．{﹣1，0，1}B．{0，1}C．{1}D．{0}2．（5分）复数z＝i（i+1）（i为虚数单位）的共轭复数是（）A．﹣1﹣iB．﹣1+iC．1﹣iD．1+i3．（5分）命题“若α＝，则tanα＝1”的逆否命题是（）A．若α≠，则tanα≠1B．若α＝，则tanα≠1C．若tanα≠1，则α≠D．若tanα≠1，则α＝4．（5分）某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能是（）A．B．C．D．5．（5分）设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系i，yi）（i＝1，2，…，n），用最小二乘法建立的回归方程为＝0.85x﹣85.71（）A．若该大学某女生身高为170cm，则可断定其体重必为58.79kgB．回归直线过样本点的中心（，）C．若该大学某女生身高增加1cm，则其体重约增加0.85kgD．y与x具有正的线性相关关系小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com6．（5分）已知双曲线C：的焦距为10，点P（2，1），则C的方程为（）A．B．C．D．7．（5分）设a＞b＞1，c＜0，给出下列三个结论：①＞；②ac＜bc；③logb（a﹣c）＞loga（b﹣c）．其中所有的正确结论的序号（）A．①B．①②C．②③D．①②③8．（5分）在△ABC中，AC＝，BC＝2，则BC边上的高等于（）A．B．C．D．9．（5分）设定义在R上的函数f（x）是最小正周期2π的偶函数，f′（x）（x）的导函数，当x∈[0，0＜f（x）＜1（0，π），且x≠时，（x﹣）f′（x），则函数y＝f（x）﹣sinx在[﹣2π（）A．2B．4C．5D．8二、填空题（共7小题，满分30分）（10-11为选做题，两题任选一题，12-16为必做题）10．（5分）在极坐标系中，曲线C1：ρ（cosθ+sinθ）＝1与曲线C2：ρ＝a（a＞0）的一个交点在极轴上，则a＝．11．某制药企业为了对某种药用液体进行生物测定，需要优选培养温度，实验范围定为29℃～63℃．精确度要求±1℃．用分数法进行优选时．12．（5分）不等式x2﹣5x+6≤0的解集为．13．（5分）如图是某学校一名篮球运动员在五场比赛中所得分数的茎叶图，则该运动员在这五场比赛中得分的方差为．（注：方差+…+，其中1，x2，…，xn的平均数）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com14．（5分）如果执行如图所示的程序框图，输入x＝4.5，则输出的数i＝．15．（5分）如图，在平行四边形ABCD中，AP⊥BD，且AP＝3，则＝．16．（5分）对于n∈N*，将n表示为n＝+…+，当i＝k时，ai＝1，当0≤i≤k﹣1时，ai为0或1．定义bn如下：在n的上述表示中，当a0，a1，a2，…，ak中等于1的个数为奇数时，bn＝1；否则bn＝0．（1）b2+b4+b6+b8＝；（2）记cm为数列{bn}中第m个为0的项与第m+1个为0的项之间的项数，则cm的最大值是．三、解答题（共6小题，满分75分）17．（12分）某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如表所示．一次购物量1至4件5至8件9至12件13至16件17件以上顾客数（人）x3025y10结算时间（分钟/人11.522.53已知这100位顾客中的一次购物量超过8件的顾客占55%．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（Ⅰ）确定x，y的值，并估计顾客一次购物的结算时间的平均值；（Ⅱ）求一位顾客一次购物的结算时间不超过2分钟的概率．（将频率视为概率）18．（12分）已知函数f（x）＝Asin（ωx+φ）（x∈R，ω＞0，0＜φ＜）的部分图象如图所示．（Ⅰ）求函数f（x）的解析式；（Ⅱ）求函数g（x）＝f（x﹣）﹣f（x+）19．（12分）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，AD∥BC，AC⊥BD．（Ⅰ）证明：BD⊥PC；（Ⅱ）若AD＝4，BC＝2，直线PD与平面PAC所成的角为30°20．（13分）某公司一下属企业从事某种高科技产品的生产．该企业第一年年初有资金2000万元，将其投入生产，到当年年底资金增长了50%．预计以后每年年增长率与第一年的相同．公司要求企业从第一年开始，并将剩余资金全部投入下一年生产．设第n年年底企业上缴资金后的剩余资金...