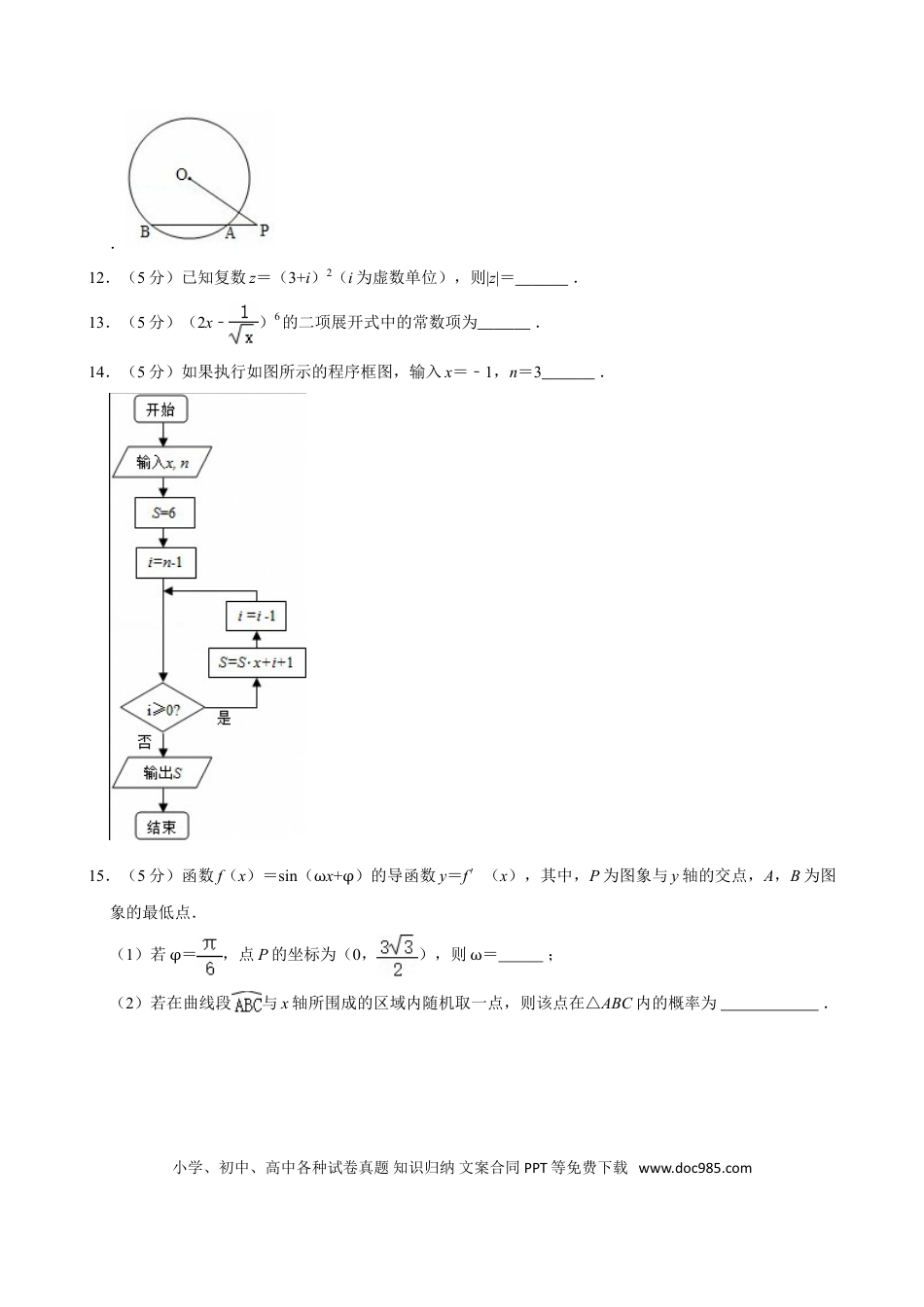
2012年湖南省高考数学试卷（理科）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）设集合M＝{﹣1，0，1}，N＝{x|x2≤x}，则M∩N＝（）A．{0}B．{0，1}C．{﹣1，1}D．{﹣1，0，1}2．（5分）命题“若α＝，则tanα＝1”的逆否命题是（）A．若α≠，则tanα≠1B．若α＝，则tanα≠1C．若tanα≠1，则α≠D．若tanα≠1，则α＝3．（5分）某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能是（）A．B．C．D．4．（5分）设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系i，yi）（i＝1，2，…，n），用最小二乘法建立的回归方程为＝0.85x﹣85.71（）A．若该大学某女生身高为170cm，则可断定其体重必为58.79kgB．回归直线过样本点的中心（，）C．若该大学某女生身高增加1cm，则其体重约增加0.85kgD．y与x具有正的线性相关关系小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com5．（5分）已知双曲线C：的焦距为10，点P（2，1），则C的方程为（）A．B．C．D．6．（5分）函数f（x）＝sinx﹣cos（x+）的值域为（）A．[﹣2，2]B．[﹣，]C．[﹣1，1]D．[﹣，]7．（5分）在△ABC中，AB＝2，AC＝3，•，则BC＝（）A．B．C．2D．8．（5分）已知两条直线l1：y＝m和l2：y＝（m＞0），l1与函数y＝|log2x|的图象从左至右相交于点A，B，l2与函数y＝|log2x|的图象从左至右相交于点C，D．记线段AC和BD在x轴上的投影长度分别为a，b，当m变化时，（）A．16B．8C．8D．4二、填空题（共8小题，考生作答7小题，满分35分，9,10,11三题任选两题作答；12～16必做题）9．在直角坐标系xoy中，已知曲线C1：（t为参数）与曲线C2：（θ为参数，a＞0）有一个公共点在x轴上，则a等于．10．（5分）不等式|2x+1|﹣2|x﹣1|＞0的解集为．11．（5分）如图，过点P的直线与圆⊙O相交于A，B两点．若PA＝1，PO＝3，则圆O的半径等于小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com．12．（5分）已知复数z＝（3+i）2（i为虚数单位），则|z|＝．13．（5分）（2x﹣）6的二项展开式中的常数项为．14．（5分）如果执行如图所示的程序框图，输入x＝﹣1，n＝3．15．（5分）函数f（x）＝sin（ωx+φ）的导函数y＝f′（x），其中，P为图象与y轴的交点，A，B为图象的最低点．（1）若φ＝，点P的坐标为（0，），则ω＝；（2）若在曲线段与x轴所围成的区域内随机取一点，则该点在△ABC内的概率为．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com16．（5分）设N＝2n（n∈N*，n≥2），将N个数x1，x2，…，xN依次放入编号为1，2，…，N的N个位置，得到排列P0＝x1x2…xN．将该排列中分别位于奇数与偶数位置的数取出，并按原顺序依次放入对应的前和后，得到排列P1＝x1x3…xN﹣1x2x4…xN，将此操作称为C变换，将P1分成两段，每段个数，得到P2，当2≤i≤n﹣2时，将Pi分成2i段，每段个数，得到Pi+1，例如，当N＝8时，P2＝x1x5x3x7x2x6x4x8，此时x7位于P2中的第4个位置．（1）当N＝16时，x7位于P2中的第个位置；（2）当N＝2n（n≥8）时，x173位于P4中的第个位置．三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．17．（12分）某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如下表所示．一次性购物量1至4件5至8件9至12件13至16件17件及以上顾客数（人）x3025y10结算时间（分钟/人）11.522.53已知这100位顾客中的一次购物量超过8件的顾客占55%．（Ⅰ）确定x，y的值，并求顾客一次购物的结算时间X的分布列与数学期望；（Ⅱ）若某顾客到达收银台时前面恰有2位顾客需结算，且各顾客的结算相互独立，求该顾客结算前的等候时间不超过2.5分钟的概率．（注：将频率视为概率）18．（12分）如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，BC＝3，AD＝5，E是CD的中点．（Ⅰ）证明：CD⊥平面PAE；（Ⅱ）若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等，求四棱锥P﹣ABCD的体积．小学、初中、...