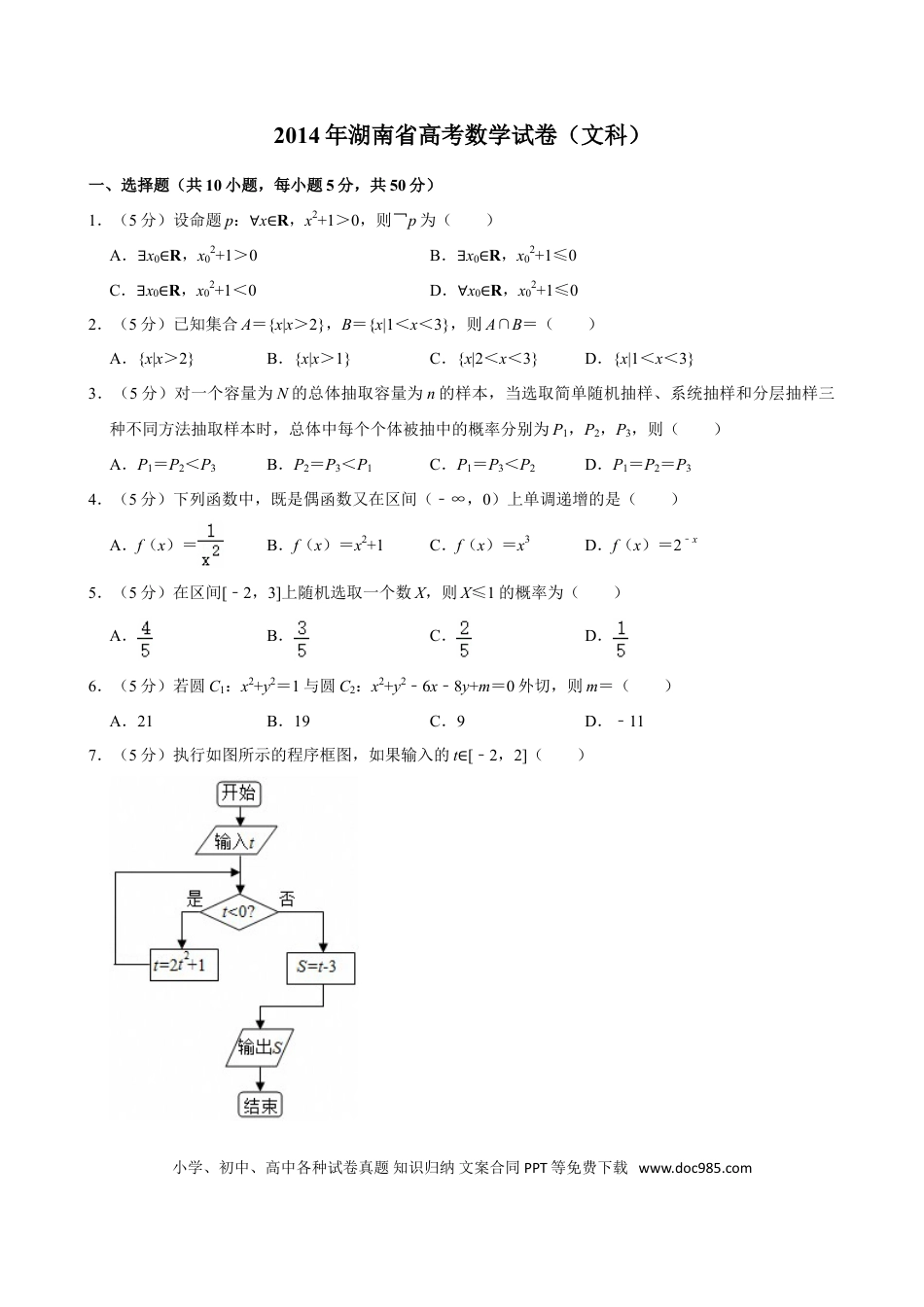
2014年湖南省高考数学试卷（文科）一、选择题（共10小题，每小题5分，共50分）1．（5分）设命题p：∀x∈R，x2+1＞0，则￢p为（）A．∃x0∈R，x02+1＞0B．∃x0∈R，x02+1≤0C．∃x0∈R，x02+1＜0D．∀x0∈R，x02+1≤02．（5分）已知集合A＝{x|x＞2}，B＝{x|1＜x＜3}，则A∩B＝（）A．{x|x＞2}B．{x|x＞1}C．{x|2＜x＜3}D．{x|1＜x＜3}3．（5分）对一个容量为N的总体抽取容量为n的样本，当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时，总体中每个个体被抽中的概率分别为P1，P2，P3，则（）A．P1＝P2＜P3B．P2＝P3＜P1C．P1＝P3＜P2D．P1＝P2＝P34．（5分）下列函数中，既是偶函数又在区间（﹣∞，0）上单调递增的是（）A．f（x）＝B．f（x）＝x2+1C．f（x）＝x3D．f（x）＝2﹣x5．（5分）在区间[﹣2，3]上随机选取一个数X，则X≤1的概率为（）A．B．C．D．6．（5分）若圆C1：x2+y2＝1与圆C2：x2+y2﹣6x﹣8y+m＝0外切，则m＝（）A．21B．19C．9D．﹣117．（5分）执行如图所示的程序框图，如果输入的t∈[﹣2，2]（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．[﹣6，﹣2]B．[﹣5，﹣1]C．[﹣4，5]D．[﹣3，6]8．（5分）一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球（）A．1B．2C．3D．49．（5分）若0＜x1＜x2＜1，则（）A．﹣＞lnx2﹣lnx1B．﹣＜lnx2﹣lnx1C．x2＞x1D．x2＜x110．（5分）在平面直角坐标系中，O为原点，A（﹣1，0），B（0，），C（3，0），动点D满足|，则|++|的取值范围是（）A．[4，6]B．[﹣1，+1]C．[2，2]D．[﹣1，+1]二、填空题（共5小题，每小题5分，共25分）11．（5分）复数（i为虚数单位）的实部等于．12．（5分）在平面直角坐标系中，曲线C：（t为参数）的普通方程为．13．（5分）若变量x，y满足约束条件，则z＝2x+y的最大值为．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com14．（5分）平面上一机器人在行进中始终保持与点F（1，0）的距离和到直线x＝﹣1的距离相等，若机器人接触不到过点P（﹣1，0），则k的取值范围是．15．（5分）若f（x）＝ln（e3x+1）+ax是偶函数，则a＝．三、解答题（共6小题，75分）16．（12分）已知数列{an}的前n项和Sn＝，n∈N*．（Ⅰ）求数列{an}的通项公式；（Ⅱ）设bn＝+（﹣1）nan，求数列{bn}的前2n项和．17．（12分）某企业有甲、乙两个研发小组，为了比较他们的研发水平，现随机抽取这两个小组往年研发新产品的结果如下：（a，b），（a，），（a，b），（，b），（，），（a，b），（a，b），（a，），（，b），（a，），（，），（a，b），（a，），（，b）（a，b）其中a，分别表示甲组研发成功和失败，b，分别表示乙组研发成功和失败．（Ⅰ）若某组成功研发一种新产品，则给该组记1分，否则记0分，并比较甲、乙两组的研发水平；（Ⅱ）若该企业安排甲、乙两组各自研发一样的产品，试估计恰有一组研发成功的概率．18．（12分）如图，已知二面角α﹣MN﹣β的大小为60°，菱形ABCD在面β内，∠BAD＝60°，E是AB的中点，垂足为O．（Ⅰ）证明：AB⊥平面ODE；（Ⅱ）求异面直线BC与OD所成角的余弦值．19．（13分）如图，在平面四边形ABCD中，DA⊥AB，EC＝，EA＝2，∠BEC＝．（Ⅰ）求sin∠CED的值；（Ⅱ）求BE的长．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com20．（13分）如图，O为坐标原点，双曲线C1：﹣＝1（a1＞0，b1＞0）和椭圆C2：+＝1（a2＞b2＞0）均过点P（，1），且以C1的两个顶点和C2的两个焦点为顶点的四边形是面积为2的正方形．（Ⅰ）求C1、C2的方程；（Ⅱ）是否存在直线l，使得l与C1交于A、B两点，与C2只有一个公共点，且|+|＝|21．（13分）已知函数f（x）＝xcosx﹣sinx+1（x＞0）．（Ⅰ）求f（x）的单调区间；（Ⅱ）记xi为f（x）的从小到大的第i（i∈N*）个零点，证明：对一切n∈N*，有++…+＜．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com