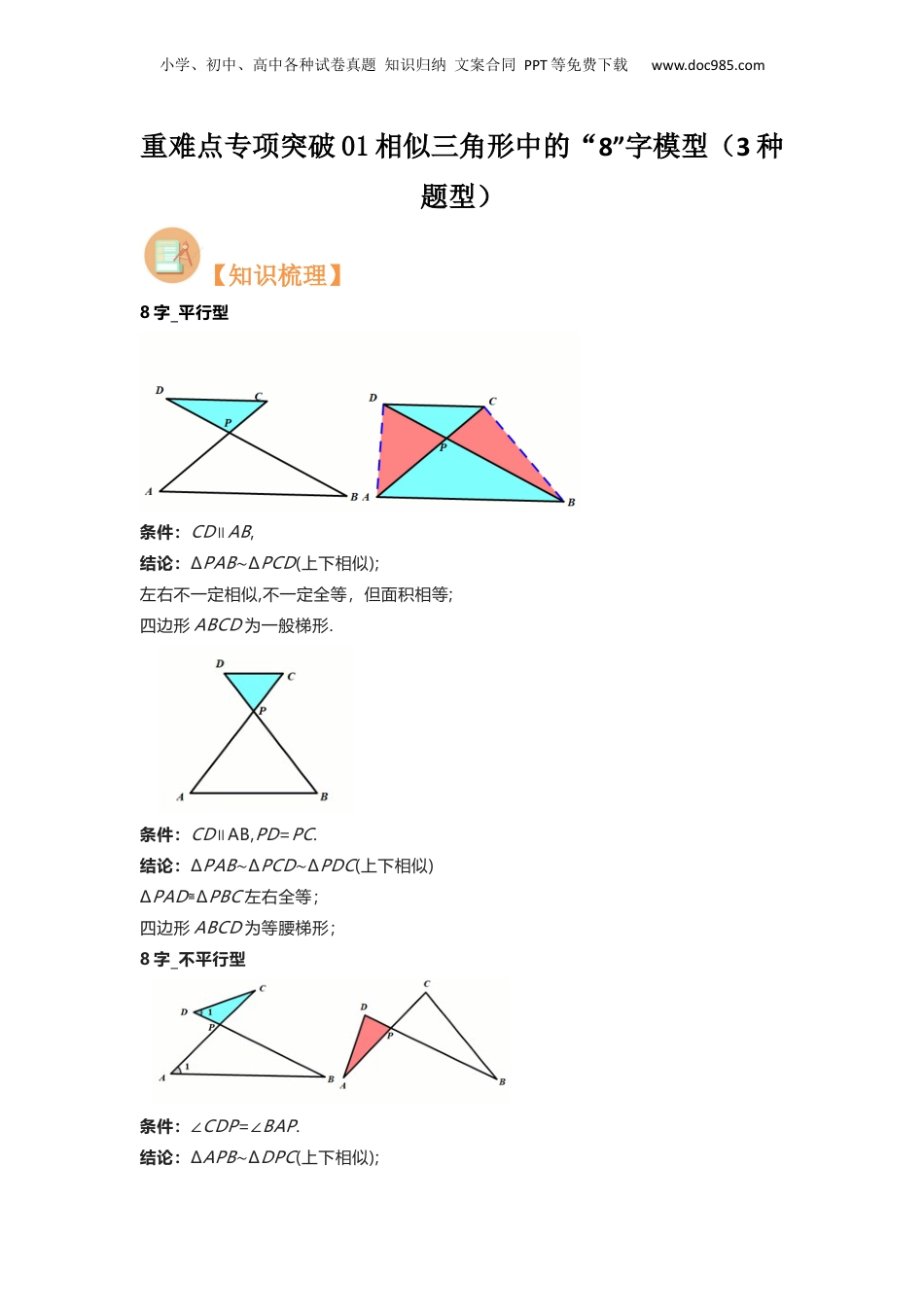
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com重难点专项突破01相似三角形中的“8”字模型（3种题型）【知识梳理】8字_平行型条件：CD∥AB,结论：ΔPAB∼ΔPCD(上下相似);左右不一定相似,不一定全等，但面积相等;四边形ABCD为一般梯形.条件：CD∥AB,PD=PC.结论：ΔPAB∼ΔPCD∼ΔPDC(上下相似)ΔPAD≅ΔPBC左右全等；四边形ABCD为等腰梯形；8字_不平行型条件：∠CDP=∠BAP.结论：ΔAPB∼ΔDPC(上下相似);小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comΔAPD∼ΔBPC(左右相似);【考点剖析】题型一：8字-平行型（1）直接利用“8”字型解题例1.如图，在平行四边形中，点在边上，若，则．【答案】．【解析】，可知，由，可知，故．【总结】初步认识相似三角形中的“8”字型．例2.如图，为对角线上任意一点．求证：．【解析】证明：四边形为平行四边形，，．根据三角形一边平行线的性质定理，则有，．【总结】初步认识相似三角形中的“8”字型，一个图形中存在往往不只一个，可用来进行等比例转化．例3.如图，在平行四边形中，的延长线上有一点，交于点，交于点．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com求证：．【解析】证明：四边形为平行四边形，，．根据三角形一边平行线的性质定理，则有：，．【总结】初步认识相似三角形中的“8”字型，一个图形中存在往往不只一个，可用来进行等比例转化．例4.如图，点在线段上，和都是等边三角形．求证：（1）；（2）．【解析】证明：（1）和是等边三角形，． 点在线段上，．，．（2）同（1）易证得，则有．和是等边三角形，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com，，．【总结】初步认识相似三角形中的“8”字型，一个图形中存在往往不只一个，可用来进行等比例转化．例5.如图，已知．，，求的长．（用、的代数式表示）．【答案】．【解析】由，则有，即，得．【总结】考查相似三角形中“8”字型的综合应用，得到比例关系．例6.如图，为平行四边形的对角线上一点，，的延长线交的延长线于点，交于点，求的值．【答案】．【解析】由，可得，即，故，由，可得：．【总结】考查相似三角形中“8”字型的综合应用，得到比例关系．例7.如图，，，，求的值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【答案】．【解析】由，得：，又，可得，故．【总结】考查相似三角形中“8”字型的综合应用，得到比例关系．（2）添加辅助线构造“8”字模型解题例8.过的顶点C任作一直线，与边AB及中线AD分别交于点F、E．求证：．【解析】过点作交于点．，；是中线，，；．【总结】题考查三角形一边的平行线知识，要学会构造平行基本模型．例9.如图，AD是的内角平分线．求证：．FEDCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【解析】过点作交的延长线于点．，是角平分线；．【总结】本题考查了三角形一边的平行线、角平分线及等腰三角形的相关知识．题型二：8字-不平行型例10.如图，∠BEC＝∠CDB，下列结论正确的是（）A．EF•BF＝DF•CFB．BE•CD＝BF•CFC．AE•AB＝AD•ACD．AE•BE＝AD•DC【分析】结合图形利用8字模型相似三角形证明△EFB∽△DFC，然后利用等角的补角相等得出∠AEC＝∠ADB，最后证明△ABD∽△ACE，利用相似三角形的对应边成比例逐一判断即可．【解答】解： ∠BEC＝∠CDB，∠EFB＝∠DFC，MDCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com∴△EFB∽△DFC，∴EFDF=FBFC，∴EF•FC＝DF•FB，故A不符合题意： △EFB∽△DFC，∴BECD=BFFC，∴BE•CF＝CD•BF，故B不符合题意； ∠BEC＝∠CDB，∠BEC+∠AEC＝180°，∠BDC+∠ADB＝180°，∴∠AEC＝∠ADB，∴△ABD∽△ACE，∴ABAC=ADAE，∴AB•AE＝AD•AC，故C符合题意；因为：AE，BE，AD，CD组不成三角形，也不存在比例关系，故D不符合题意；故选：C．【点评】本题考查了相似三角形的判定与性质，根据题目的已知条件并结合图形分析是解题的关键．【过关检测】一．选择题...