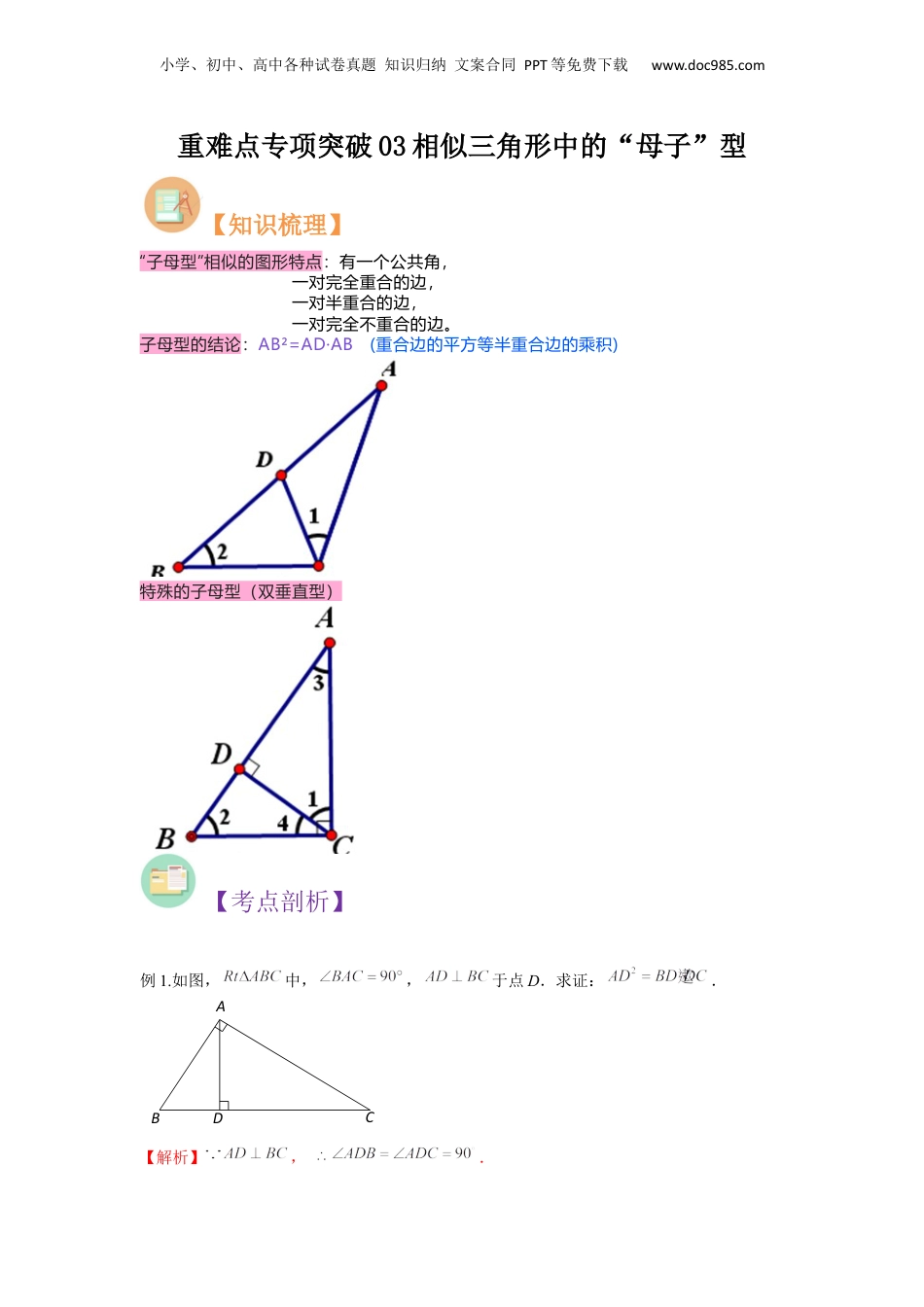
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com重难点专项突破03相似三角形中的“母子”型【知识梳理】“子母型”相似的图形特点：有一个公共角，一对完全重合的边，一对半重合的边，一对完全不重合的边。子母型的结论：AB²=AD·AB(重合边的平方等半重合边的乘积)特殊的子母型（双垂直型）【考点剖析】例1.如图，中，，于点D．求证：．【解析】，．DCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com．，，．，．．【总结】本题考查相似三角形的性质及判定等知识例2.如图，，于点，，，求的长．【答案】．【解析】，，，．根据面积法，可知，解得．又，，可得．，代入可得：．，，．代入得：．【总结】考查对于“子母三角形”的认识，初步建立可将相似三角形中可将对应边之比转化为同一三角形中边长比的思想，实际上这个这个图形中包含5个直角三角形，全部都是两相似．例3．如图，在△ABC中，点D在边AB上，点E、点F在边AC上，且DEBC，．（1）求证：DFBE；（2）如且AF＝2，EF＝4，AB＝6．求证△ADE∽△AEB．EDCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【分析】（1）由题意易得，则有，进而问题可求证；（2）由（1）及题意可知，然后可得，进而可证，最后问题可求证．【详解】解：（1） DEBC，∴， ，∴，∴DFBE；（2） AF＝2，EF＝4，∴由（1）可知，，AE=6， AB＝6，∴，∴，∴， ∠A=∠A，∴△ADE∽△AEB．【点睛】本题主要考查相似三角形的判定，熟练掌握相似三角形的判定方法是解题的关键．例4.已知：如图，四边形ABCD是平行四边形，在边AB的延长线上截取BE＝AB，点F在AE的延长线上，CE和DF交于点M，BC和DF交于点N，联结BD．（1）求证：△BND∽△CNM；（2）如果AD2＝AB•AF，求证：CM•AB＝DM•CN．【分析】（1）利用平行四边形的性质得AB=CD，AB∥CD，再证明四边形BECD为平行四边小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com形得到BD∥CE，根据相似三角形的判定方法，由CM∥DB可判断△BND∽△CNM；（2）先利用AD2=AB•AF可证明△ADB∽△AFD，则∠1=∠F，再根据平行线的性质得∠F=4∠，∠2=3∠，所以∠3=4∠，加上∠NMC=∠CMD，于是可判断△MNC∽△MCD，所以MC：MD=CN：CD，然后利用CD=AB和比例的性质即可得到结论．【详解】证明：（1） 四边形ABCD是平行四边形，∴AB=CD，AB∥CD，而BE=AB，∴BE=CD，而BE∥CD，∴四边形BECD为平行四边形，∴BD∥CE， CM∥DB，∴△BND∽△CNM；（2） AD2=AB•AF，∴AD：AB=AF：AD，而∠DAB=∠FAD，∴△ADB∽△AFD，1=∴∠∠F， CD∥AF，BD∥CE，∴∠F=4∠，∠2=3∠，3=4∴∠∠，而∠NMC=∠CMD，∴△MNC∽△MCD，∴MC：MD=CN：CD，∴MC•CD=MD•CN，而CD=AB，∴CM•AB=DM•CN．【点睛】本题考查了三角形相似的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用，寻找相似三角形的小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com一般方法是通过作平行线构造相似三角形．在运用相似三角形的性质时主要利用相似比计算线段的长．也考查了平行四边形的判定与性质．例5.如图，已知在△ABC中，BC＞AB，BD平分∠ABC，交边AC于点D，E是BC边上一点，且BE＝BA，过点A作AG∥DE，分别交BD、BC于点F、G，联结FE．（1）求证：四边形AFED是菱形；（2）求证：AB2＝BG•BC；（3）若AB＝AC，BG＝CE，联结AE，求的值．【分析】（1）由题目条件可证得△ABF≌△EBF（SAS）及△ABD≌△EBD（SAS），进而可推出AF＝FE＝ED＝DA，可得出四边形AFED是菱形．（2）根据条件可证得△ABG∽△CBA，即可证明结论．（3）由条件可得△DAE∽△ABC，由相似比可得，由BE2＝EC•BC，得到点E是BC的黄金分割点，可得出，即可得出结论．【详解】（1）证明： BD平分∠ABC，∴∠ABF＝∠EBF， BA＝BE，BF＝BF，∴△ABF≌△EBF（SAS），∴AF＝EF，同理可得△ABD≌△EBD（SAS），∴AD＝ED，∠ADB＝∠EDB， AG∥DE，∴∠AFD＝∠EDF，∴∠AFD＝∠ADF，∴AF＝AD，∴A...