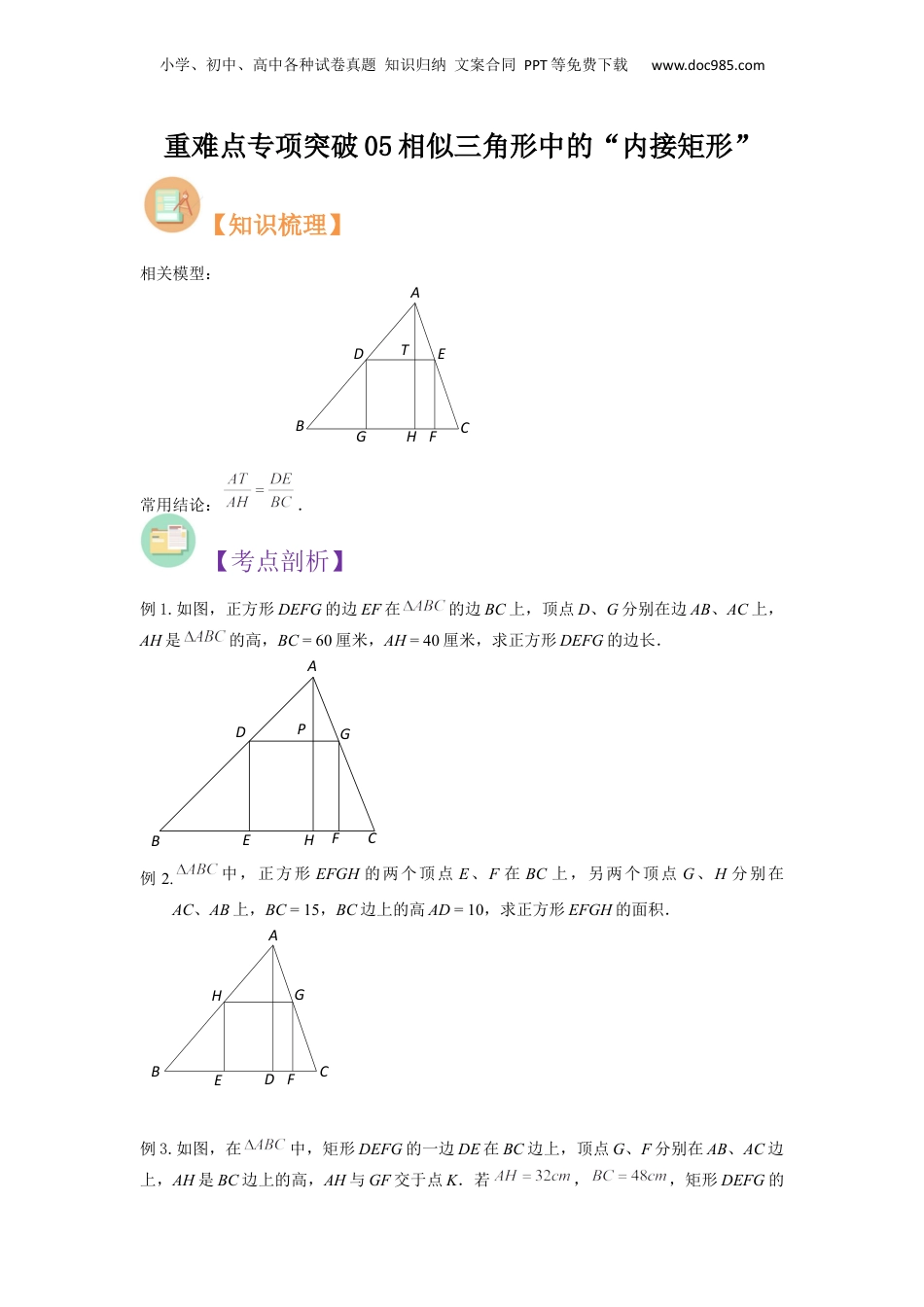
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com重难点专项突破05相似三角形中的“内接矩形”【知识梳理】相关模型：常用结论：．【考点剖析】例1.如图，正方形DEFG的边EF在的边BC上，顶点D、G分别在边AB、AC上，AH是的高，BC=60厘米，AH=40厘米，求正方形DEFG的边长．例2.中，正方形EFGH的两个顶点E、F在BC上，另两个顶点G、H分别在AC、AB上，BC=15，BC边上的高AD=10，求正方形EFGH的面积．例3.如图，在中，矩形DEFG的一边DE在BC边上，顶点G、F分别在AB、AC边上，AH是BC边上的高，AH与GF交于点K．若，，矩形DEFG的PHGFEDCBADEFGHCBATHGFEDCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com周长为76cm，求矩形DEFG的面积．例4.在锐角中，矩形DEFG的顶点D在AB边上，顶点E、F在BC边上，顶点G在AC边上，如果矩形DEFG的长为6，宽为4，设底边BC上的高为x，的面积为y，求y与x的函数关系式．例5.如图，矩形DEFG的边EF在的边BC上，顶点D、G分别在边AB、AC上，AH为BC边上的高，AH交DG于点P，已知，，设DG的长为x，矩形DEFG的面积为y，求y关于x的函数解析式及其定义域．例6.一块直角三角形木板的一条直角边AB长为1.5m，面积为1.5m2，现需把它加工成一个面积最大的正方形桌面，请甲、乙两位同学设计加工方案，甲设计方案如图（1），乙设计KHGFEDCBAPHDGFECBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com方案如图（2）．你认为哪位同学设计的方案较好？请说明理由（加工损耗忽略不计，计算结果中可保留分数）．【过关检测】一、单选题1．（2023·上海浦东新·统考二模）如图，已知正方形的顶点D、E在的边上，点G、F分别在边上，如果，的面积是32，那么这个正方形的边长是（）A．4B．8C．D．2．（2022秋·上海奉贤·九年级校考期中）如图，正方形的边在的边上，顶点D、G分别在边上，已知的边长15厘米，高为10厘米，则正方形的边长是（）A．4厘米B．5厘米C．6厘米D．8厘米二、填空题3．（2021秋·上海·九年级校考阶段练习）如图，在中，，正方形的小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com边在边上，顶点D、E分别在、上，，若的面积为36，则的长为______．4．（2021秋·上海闵行·九年级统考期中）如图，已知正方形DEFG的顶点D、E在△ABC的边BC上，顶点G、F分别在边AB、AC上，如果BC＝4，BC边上的高是6，那么这个正方形的边长是____．5．（2023·上海长宁·统考一模）如图，在中，，正方形的边在的边上，顶点、分别在边、上，如果其面积为24，那么的值为______．6．（2022秋·上海·九年级上外附中校考阶段练习）如图，矩形为的内接矩形，点G，F分别在上，是边上的高，，则矩形的面积为___________．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com7．（2022秋·上海青浦·九年级校考期中）如图，矩形内接于，，，，则边上的高的长是______8．（2022秋·上海静安·九年级校考期中）如图，已知在中，边，高，正方形的顶点F、G在边BC上，顶点E、H分别在边AB和AC上，那么这个正方形的面积等于________．9．（2022秋·上海松江·九年级校考期中）如图：正方形的边在边上，顶点D、G分别在边、上，于H，交于P，已知，，那么正方形的边长为___________．10．（2022秋·上海浦东新·九年级校考期中）如图，正方形的边在的边上，顶点、分别在边、上．已知长为40厘米，若正方形的边长为25厘米，则的高为________厘米．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com11．（2022秋·上海·九年级校考期中）如图，已知正方形的顶点、分别在的边、上，顶点、在的边上，若，，那么这个正方形的边长是________．12．（2023·上海徐汇·统考一模）如图，在中，，，，正方形内接于，点、分别在边、上，点、在斜边上，那么正方形的边长是______．13．（2022春·上海·八年级专题练习）如图，矩形DEFG的边DE在△ABC的边BC上，顶点G、F分别在边AB、AC上，已知BC＝6cm，DE＝3cm，EF＝2cm，那么边BC上的高的长是___cm．14．（2021秋·上海闵...