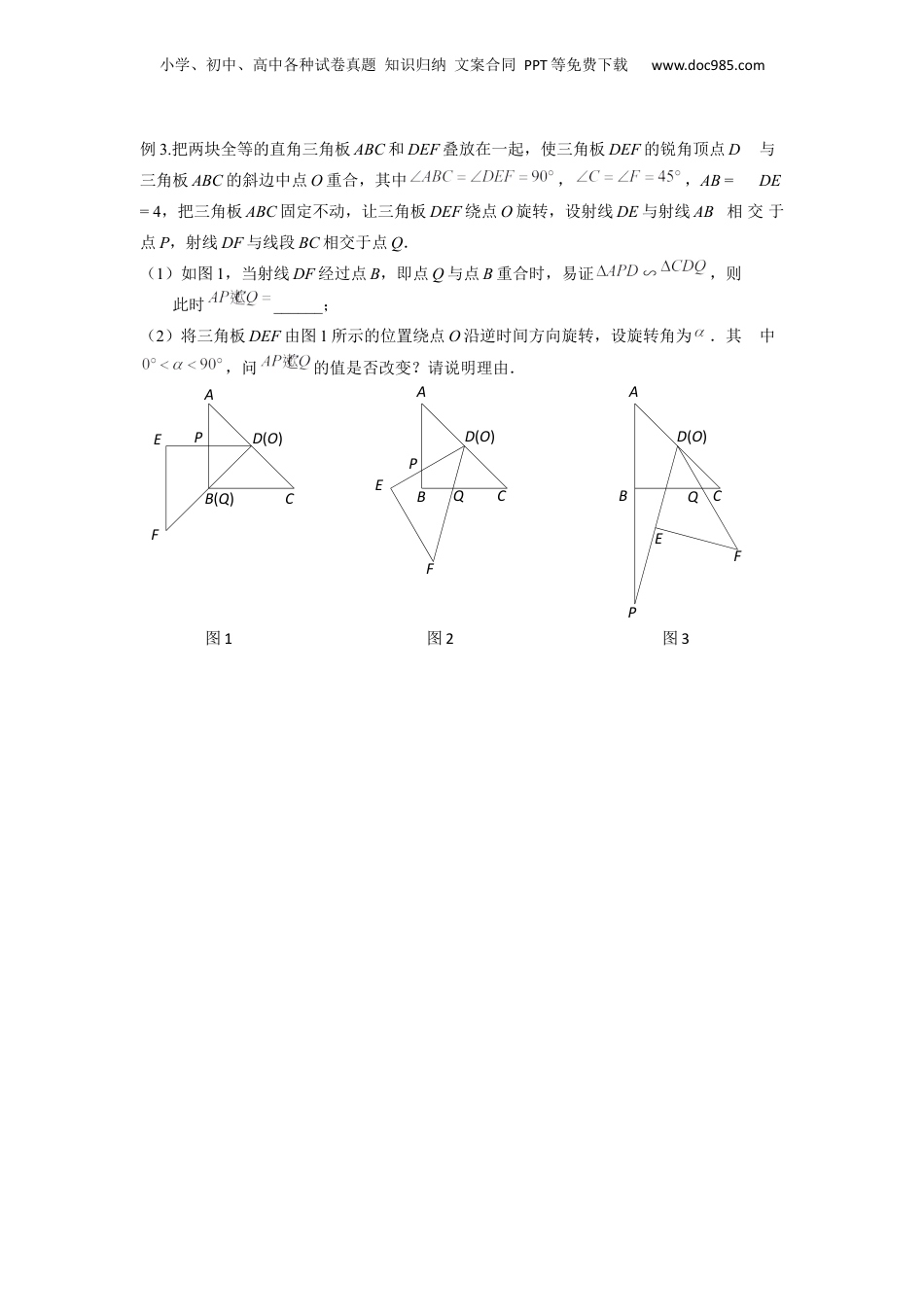
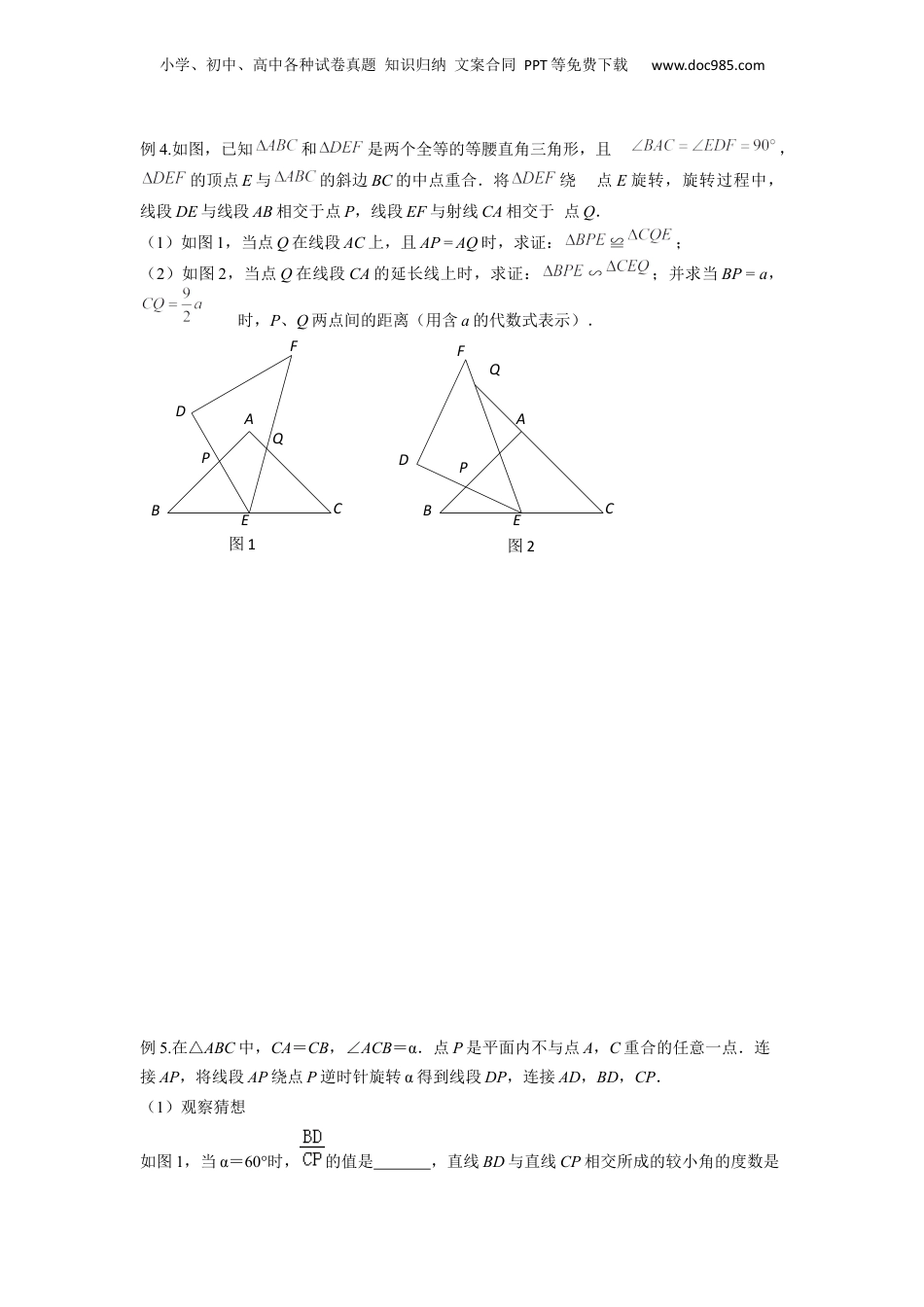
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com重难点专项突破06相似三角形中的“手拉手”旋转模型【知识梳理】“手拉手”旋转型模型展示：如图，若△ABC∽△ADE，则△ABD∽△ACE.[来.Com]【考点剖析】例1.如图，直角梯形ABCD中，，AD//BC，BC=CD，E为梯形内一点，且，将绕点C旋转90°使BC与DC重合，得到，联结EF交CD于M．已知BC=5，CF=3，则DM:MC的值为（）A．B．C．D．例2、如图，D为△ABC内一点，E为△ABC外一点，且∠ABC＝∠DBE，∠3＝∠4.求证：(1)△ABD∽△CBE；(2)△ABC∽△DBE.MFEDCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com例3.把两块全等的直角三角板ABC和DEF叠放在一起，使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合，其中，，AB=DE=4，把三角板ABC固定不动，让三角板DEF绕点O旋转，设射线DE与射线AB相交于点P，射线DF与线段BC相交于点Q．（1）如图1，当射线DF经过点B，即点Q与点B重合时，易证∽，则此时______；（2）将三角板DEF由图1所示的位置绕点O沿逆时间方向旋转，设旋转角为．其中，问的值是否改变？请说明理由．图3图2图1FEFEQPQD(O)CBAD(O)CBAPPED(O)CB(Q)AF小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com例4.如图，已知和是两个全等的等腰直角三角形，且，的顶点E与的斜边BC的中点重合．将绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．（1）如图1，当点Q在线段AC上，且AP=AQ时，求证：≌；（2）如图2，当点Q在线段CA的延长线上时，求证：∽；并求当BP=a，时，P、Q两点间的距离（用含a的代数式表示）．例5.在△ABC中，CA＝CB，∠ACB＝α．点P是平面内不与点A，C重合的任意一点．连接AP，将线段AP绕点P逆时针旋转α得到线段DP，连接AD，BD，CP．（1）观察猜想如图1，当α＝60°时，的值是，直线BD与直线CP相交所成的较小角的度数是Q图2图1QPPFEDCBAFEDCBA小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com．（2）类比探究如图2，当α＝90°时，请写出的值及直线BD与直线CP相交所成的小角的度数，并就图2的情形说明理由．（3）解决问题当α＝90°时，若点E，F分别是CA，CB的中点，点P在直线EF上，请直接写出点C，P，D在同一直线上时的值．【过关检测】一．填空题（共1小题）1．（2022秋•黄浦区期末）如图，在矩形ABCD中，过点D作对角线AC的垂线，垂足为E，过点E作BE的垂线，交边AD于点F，如果AB＝3，BC＝5，那么DF的长是．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com二．解答题（共7小题）2．（2022秋•杨浦区期中）如图，已知在Rt△ABC中，∠ACB＝90°，点D在边AC上，联结BD，以BD为斜边作等腰直角三角形BDE（点E在直线BD右侧），联结CE．（1）如果∠A＝45°，求证：△ABD∽△CBE；（2）如果BC＝12，CD＝5，求线段CE的长．3．（2021春•徐汇区校级期末）如图，∠1＝∠2，AD＝AE，∠B＝∠ACE，且B、C、D三点在一条直线上，若∠B＝60°．（1）△BAD与△CAE是否全等，请说明理由；（2）△ABC是否是等边三角形，如果是．请说明理由；（3）CE＝AC+CD是否成立，如果成立请说明理由．4．（2022•静安区二模）如图①，已知梯形ABCD中，AD∥BC，∠A＝90°，AB＝，AD＝6，BC＝7，点P是边AD上的动点，联结BP，作∠BPF＝∠ADC，设射线PF交线段BC于E，交射线DC于F．（1）求∠ADC的度数；（2）如果射线PF经过点C（即点E、F与点C重合，如图②所示），求AP的长；（3）设AP＝x，DF＝y，求y关于x的函数解析式，并写出定义域．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com5．（2023•静安区校级一模）在等腰直角△ABC中，∠C＝90°，AC＝4，点D为射线CB上一动点（点D不与点B、C重合），以AD为腰且在AD的右侧作等腰直角△ADF，∠ADF＝90°，射线AB与射线FD交于点E，联结BF．（1）如图所示，当点D在线段CB上时，①求证：△ACD∽△ABF；②设CD＝x，tan∠BFD＝y，求y关于x的函数解析式，并写出x的取值范围；（2）当AB＝2BE时，求CD的长．小学、初中、高中各种试...