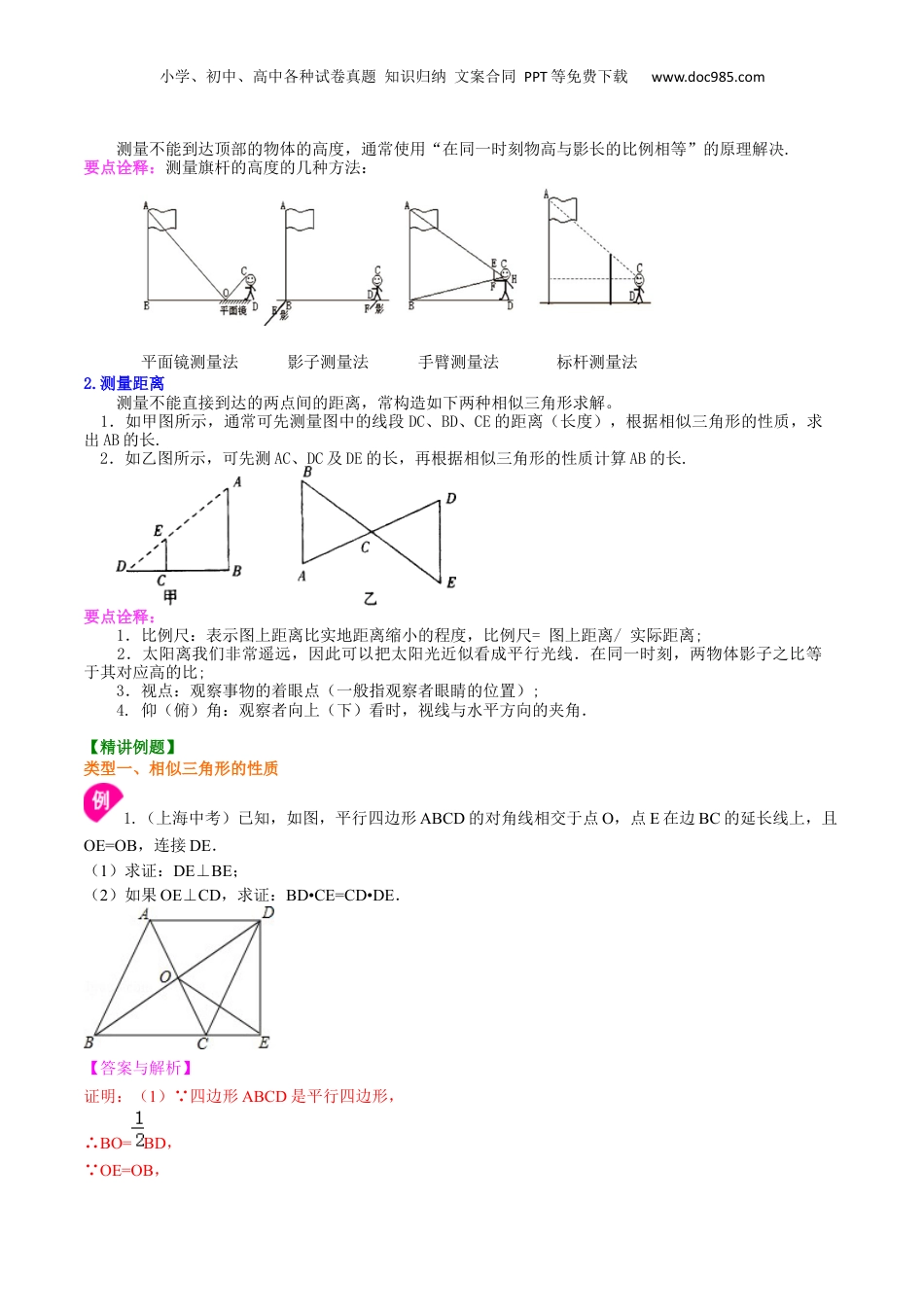
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题06相似三角形的性质（基础）【目标导向】1、探索相似三角形的性质，能运用性质进行有关计算；2、通过典型实例认识现实生活中物体的相似，能运用图形相似的知识解决一些简单的实际问题（如何把实际问题抽象为数学问题）.【知识点精讲梳理】要点一、相似三角形的性质1．相似三角形的对应角相等，对应边的比相等.2.相似三角形中的重要线段的比等于相似比.相似三角形对应高，对应中线，对应角平分线的比都等于相似比.要点诠释：要特别注意“对应”两个字，在应用时，要注意找准对应线段.3.相似三角形周长的比等于相似比∽，则由比例性质可得：4.相似三角形面积的比等于相似比的平方∽，则分别作出与的高和，则21122=1122ABCABCBCADkBCkADSkSBCADBCAD△△要点诠释：相似三角形的性质是通过比例线段的性质推证出来的.要点二、相似三角形的应用1.测量高度小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com测量不能到达顶部的物体的高度，通常使用“在同一时刻物高与影长的比例相等”的原理解决.要点诠释：测量旗杆的高度的几种方法：平面镜测量法影子测量法手臂测量法标杆测量法2.测量距离测量不能直接到达的两点间的距离，常构造如下两种相似三角形求解。1．如甲图所示，通常可先测量图中的线段DC、BD、CE的距离（长度），根据相似三角形的性质，求出AB的长.2．如乙图所示，可先测AC、DC及DE的长，再根据相似三角形的性质计算AB的长.要点诠释：1．比例尺：表示图上距离比实地距离缩小的程度，比例尺=图上距离/实际距离;2．太阳离我们非常遥远，因此可以把太阳光近似看成平行光线．在同一时刻，两物体影子之比等于其对应高的比;3．视点：观察事物的着眼点（一般指观察者眼睛的位置）;4.仰（俯）角：观察者向上（下）看时，视线与水平方向的夹角．【精讲例题】类型一、相似三角形的性质1.（上海中考）已知，如图，平行四边形ABCD的对角线相交于点O，点E在边BC的延长线上，且OE=OB，连接DE．（1）求证：DE⊥BE；（2）如果OE⊥CD，求证：BD•CE=CD•DE．【答案与解析】证明：（1） 四边形ABCD是平行四边形，∴BO=BD， OE=OB，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com∴OE=BD，∴∠BED=90°，∴DE⊥BE；（2） OE⊥CD∴∠CEO+∠DCE=∠CDE+∠DCE=90°，∴∠CEO=∠CDE， OB=OE，∴∠DBE=∠CDE， ∠BED=∠BED，∴△BDE∽△DCE，∴，∴BD•CE=CD•DE．【总结升华】本题综合性较强，考查了相似三角形、直角三角形以及平行四边形相关知识，而熟记定理是解题的关键．举一反三【变式】（铜仁市）如图，在平行四边形ABCD中，点E在边DC上，DE：EC=3：1，连接AE交BD于点F，则△DEF的面积与△BAF的面积之比为（）A．3：4B．9：16C．9：1D．3：1【答案】B．提示： 四边形ABCD为平行四边形，∴DC∥AB，∴△DFE∽△BFA， DE：EC=3：1，∴DE：DC=1=3：4，∴DE：AB=3：4，∴S△DFE：S△BFA=9：16．故选：B．2.（本溪）如图，△ABC中，AC=6，AB=4，点D与点A在直线BC的同侧，且∠ACD=∠ABC，CD=2，点E是线段BC延长线上的动点，当△DCE和△ABC相似时，线段CE的长为．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【思路点拨】根据题目中的条件和三角形的相似，可以求得CE的长，本题得以解决．【答案】3或．【解析】解： △DCE∽△ABC，∠ACD=∠ABC，AC=6，AB=4，CD=2，∴∠A=∠DCE，∴或即或解得，CE=3或CE=故答案为：3或．【总结升华】本题考查相似三角形的性质，解题的关键是明确题意，找出所求问题需要的条件，利用三角形的相似解答．举一反三：【变式】有同一三角形地块的甲、乙两地图，比例尺分别为1∶200和1∶500，求：甲地图与乙地图的相似比和面积比.【答案】设原地块为△ABC，地块在甲图上为△A1B1C1，在乙图上为△A2B2C2.∴△ABC∽△A1B1C1∽△A2B2C2且，，∴，∴.类型二、相似三角形的应用3.如图，我们想要测量河两岸相对应两点A、B之间的距离(即河宽)，你有什么方法？小...