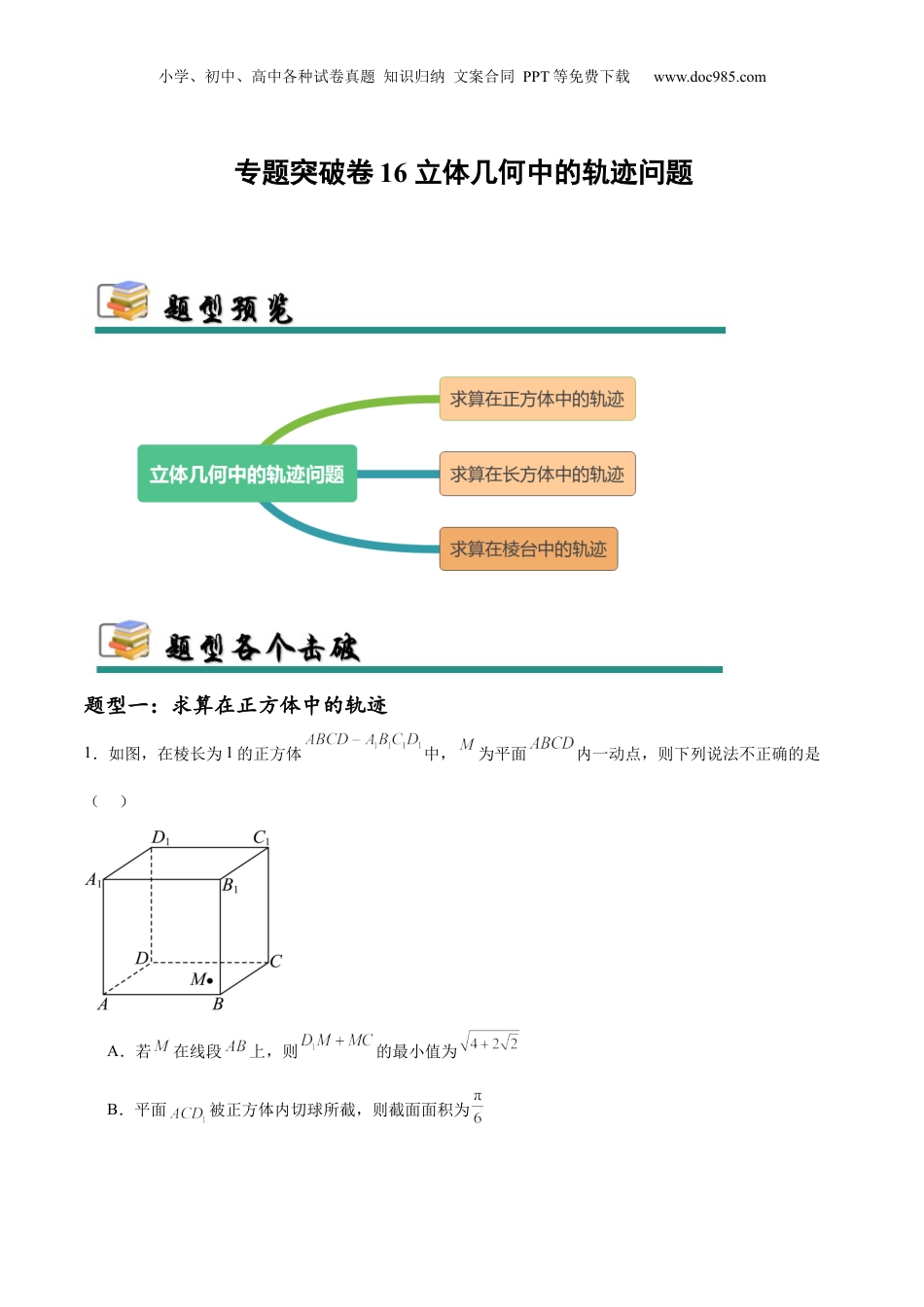
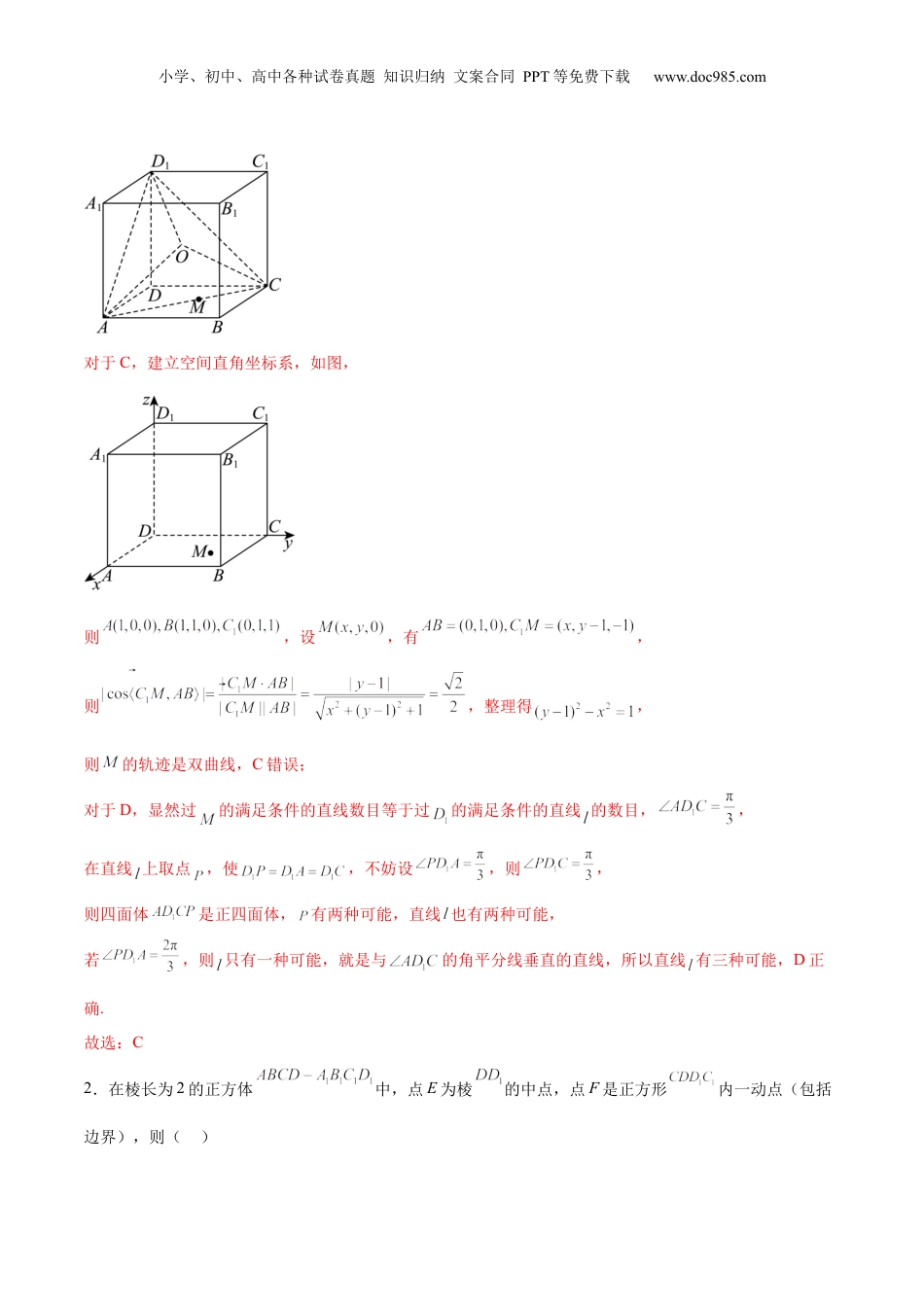
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题突破卷16立体几何中的轨迹问题题型一：求算在正方体中的轨迹1．如图，在棱长为1的正方体中，为平面内一动点，则下列说法不正确的是（）A．若在线段上，则的最小值为B．平面被正方体内切球所截，则截面面积为小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC．若与所成的角为，则点的轨迹为椭圆D．对于给定的点，过有且仅有3条直线与直线所成角为【答案】C【分析】把矩形与正方形置于同一平面，求出长判断A；求出内切球球心到平面，求出截面小圆半径判断B；建立空间直角坐标系，利用异面直线夹角建立方程判断C；利用异面直线所成角的意义转化判断D.【详解】对于A，正方体的对角面是矩形，把矩形与正方形置于同一平面，且在直线两侧，连接，则，当且仅当为与的交点时取等号，A正确；对于B，令正方体内切球球心为，连接，为正方体的中心，，，正半径，正三棱锥底面上的高，又球的半径为，则被截得的圆的半径为，面积为，B正确；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com对于C，建立空间直角坐标系，如图，则，设，有，则，整理得，则的轨迹是双曲线，C错误；对于D，显然过的满足条件的直线数目等于过的满足条件的直线的数目，，在直线上取点，使，不妨设，则，则四面体是正四面体，有两种可能，直线也有两种可能，若，则只有一种可能，就是与的角平分线垂直的直线，所以直线有三种可能，D正确.故选：C2．在棱长为2的正方体中，点E为棱的中点，点F是正方形内一动点（包括边界），则（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．三棱锥的体积为定值B．若平面，则点F的轨迹长度是C．当点Q在直线上运动时，的最小值是D．若点F是棱的中点，则平面截正方体所得截面的周长为【答案】AB【分析】对A：由平面平行可得点到平面的距离为定值，结合体积公式即可得；对B：借助线面平行的判定定理与性质定理与面面平行的性质定理可得平面平面，计算即可得点F的轨迹长度；对C：将沿翻折到与在同一个平面，借助两点之间线段最短计算即可得；对D：画出截面图形后计算即可得.【详解】对于A：平面平面，则点到平面的距离为定值2，则，故A正确；对于B：如图1，分别取中点，连接，则，且，又，，故且，所以四边形是平行四边形，所以，因为平面平面，所以平面，同理，有平面，因为且都在面，所以平面平面，因为平面平面，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以点的轨迹是线段，其长度为，故B正确；对于C，把沿翻折到与在同一个平面(如图2所示)，连接，则是的最小值，其中是边长为的等边三角形，是直角边为2的等腰直角三角形，由对称性得，即的最小值是，故C错误；对于D：如图3，由B选项知，四边形就是平面截正方体所得截面的图形，其周长为，故D错误.故选：AB.3．已知正方体的棱长为1，点满足，其中，，则（）A．当时，则的最小值为B．过点在平面内一定可以作无数条直线与垂直C．若与所成的角为，则点的轨迹为双曲线小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comD．当，时，正方体经过点、、的截面面积的取值范围为【答案】ACD【分析】对A，将平面展开到与同一平面，由两点间线段最短得解；对B，当在时，过点只能作一条直线与垂直，可判断；对CD，以点D为坐标原点建立空间直角坐标系，设出点P坐标，利用向量的坐标运算即可判断.【详解】对于A，当时，，所以点在线段上，如图，将三角形与矩形沿展成平面图形如下所示，则线段即为的最小值，利用余弦定理可知，所以，即的最小值为，故A正确；对于B，当在时，过点在平面内只可以作一条直线与垂直，故B错误；对于C，以D为原点，分别以为x轴，y轴，z轴建立空间直角坐标系，则，得，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com，整理得，为双曲线方程，故C正确．对于D，当时，，故点在线段上运动,正方体经过点、、的截面为平行四边形，以为坐标原点，建立如图所示的空间直角坐标系...