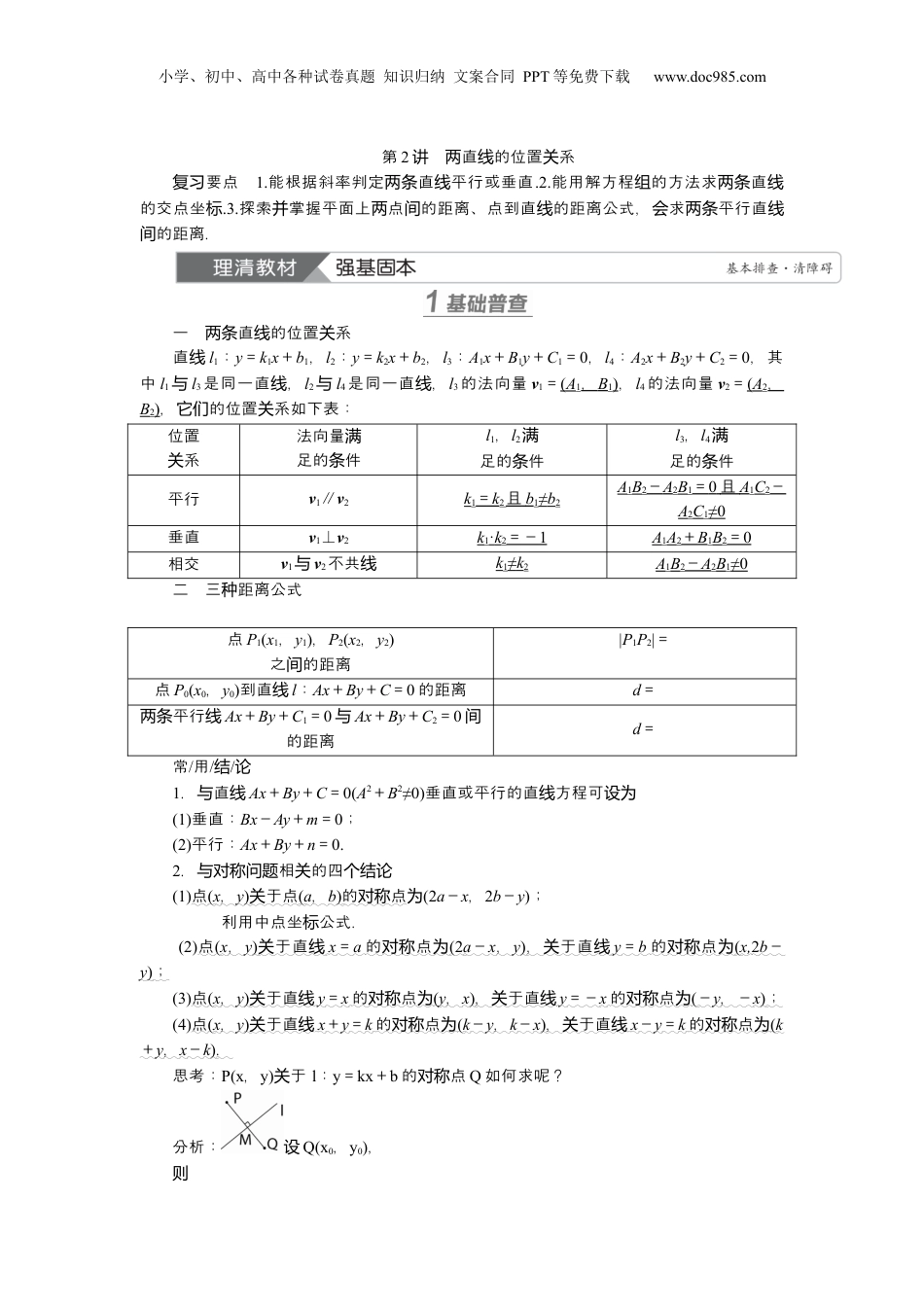
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第2直的位置系讲两线关要点复习1.能根据斜率判定直平行或垂直两条线.2.能用解方程的方法求直组两条线的交点坐标.3.探索掌握平面上点的距离、点到直的距离公式，求平行直并两间线会两条线的距离．间一直的位置系两条线关直线l1：y＝k1x＋b1，l2：y＝k2x＋b2，l3：A1x＋B1y＋C1＝0，l4：A2x＋B2y＋C2＝0，其中l1与l3是同一直，线l2与l4是同一直，线l3的法向量v1＝(A1，B1)，l4的法向量v2＝(A2，B2)，的位置系如下表：它们关位置系关法向量满足的件条l1，l2满足的件条l3，l4满足的件条平行v1∥v2k1＝k2且b1≠b2A1B2－A2B1＝0且A1C2－A2C1≠0垂直v1⊥v2k1·k2＝－1A1A2＋B1B2＝0相交v1与v2不共线k1≠k2A1B2－A2B1≠0二三距离公式种点P1(x1，y1)，P2(x2，y2)之的距离间|P1P2|＝点P0(x0，y0)到直线l：Ax＋By＋C＝0的距离d＝平行两条线Ax＋By＋C1＝0与Ax＋By＋C2＝0间的距离d＝常/用/结/论1．直与线Ax＋By＋C＝0(A2＋B2≠0)垂直或平行的直方程可线设为(1)垂直：Bx－Ay＋m＝0；(2)平行：Ax＋By＋n＝0.2．相的四与对称问题关个结论(1)点(x，y)于点关(a，b)的点对称为(2a－x，2b－y)；利用中点坐公式．标(2)点(x，y)于直关线x＝a的点对称为(2a－x，y)，于直关线y＝b的点对称为(x,2b－y)；(3)点(x，y)于直关线y＝x的点对称为(y，x)，于直关线y＝－x的点对称为(－y，－x)；(4)点(x，y)于直关线x＋y＝k的点对称为(k－y，k－x)，于直关线x－y＝k的点对称为(k＋y，x－k)．思考：P(x，y)于关l：y＝kx＋b的点对称Q如何求呢？分析：设Q(x0，y0)，则小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com1．判下列是否正确．断结论(1)若直的斜率相等，直平行，反之，亦然．两线则两线()(2)如果直两条线l1与l2垂直，那的斜率之一定等于－么它们积1.()(3)已知直线l1：A1x＋B1y＋C1＝0(其中A1，B1不同时为0)，l2：A2x＋B2y＋C2＝0(其中A2，B2不同时为0)，若A1B2－A2B1＝0，直则线l1∥l2.()(4)直外一点直上点的距离的最小就是点到直的距离．线与线值线(√)2．(2024·吉林春模长拟)已知直线l点经过(1，－1)，且直与线2x－y－5＝0垂直，则直线l的方程为()A．2x＋y－1＝0B．x－2y－3＝0C．x＋2y＋1＝0D．2x－y－3＝0解析： 直线l直与线2x－y－5＝0垂直，∴直设线l的方程为x＋2y＋c＝0， 直线l点经过(1，－1)，∴1－2＋c＝0，即c＝1.直线l的方程为x＋2y＋1＝0.故选C.答案：C3．已知点A点与B(1,2)于直关线x＋y＋3＝0，点对称则A的坐标为()A．(3,4)B．(4,5)C．(－4，－3)D．(－5，－4)解析：点设A(a，b)， 点A点与B(1,2)于直关线x＋y＋3＝0，对称∴解得点则A的坐标为(－5，－4)．故选D.答案：D4．已知直线l1：x＋ay＝1，l2：ax＋y＝1，若l1∥l2，则a＝________，此时l1与l2之间的距离为________．解析：由l1∥l2可知a2－1＝0，即a＝±1.又当a＝1，时l1与l2重合，不符合意．所以题a＝－1，此时l1：x－y－1＝0，l2：x－y＋1＝0.所以l1与l2的距离d＝＝.答案：－1型题直的平行垂直两条线与典例1(1)已知点经过A(－2,0)和点B(1,3a)的直线l1点与经过P(0，－1)和点Q(a，－2a)的直线l2互相垂直，则实数a的值为________．(2)已知直两线l1：x＋my＋6＝0，l2：(m－2)x＋3y＋2m＝0，若l1∥l2，求m的．值先由A1B2－A2B1＝0求出m，再回代验证(排除重合)．(1)解析：方法一：l1的斜率k1＝＝a.当a≠0，时l2的斜率k2＝＝.因为l1⊥l2，所以k1k2＝－1，即a·＝－1，解得a＝1.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com当a＝0，得时P(0，－1)，Q(0,0)，直这时线l2为y，轴A(－2,0)，B(1,0)，直线l1为x，然轴显l1⊥l2.上可知，综实数a的值为1或0.方法二：AB＝(3,3a)，PQ＝(a,1－2a)，由AB⊥PQ可知AB·PQ＝3a＋3a－6a2＝0，解得a＝0或1.故答案为1或0.(2)解：若l1∥l2，易知m≠0，－＝－且－≠－，则∴m＝－1.直位置系的判定方法两线关(1)已知直的斜率存在两线①直平行两线⇔直的斜率相等且坐上的截距不相等；两线标轴②直垂直两线⇔直的斜率之－两线积为1.(2)已知直的斜率不存在两线若直的斜率不存...