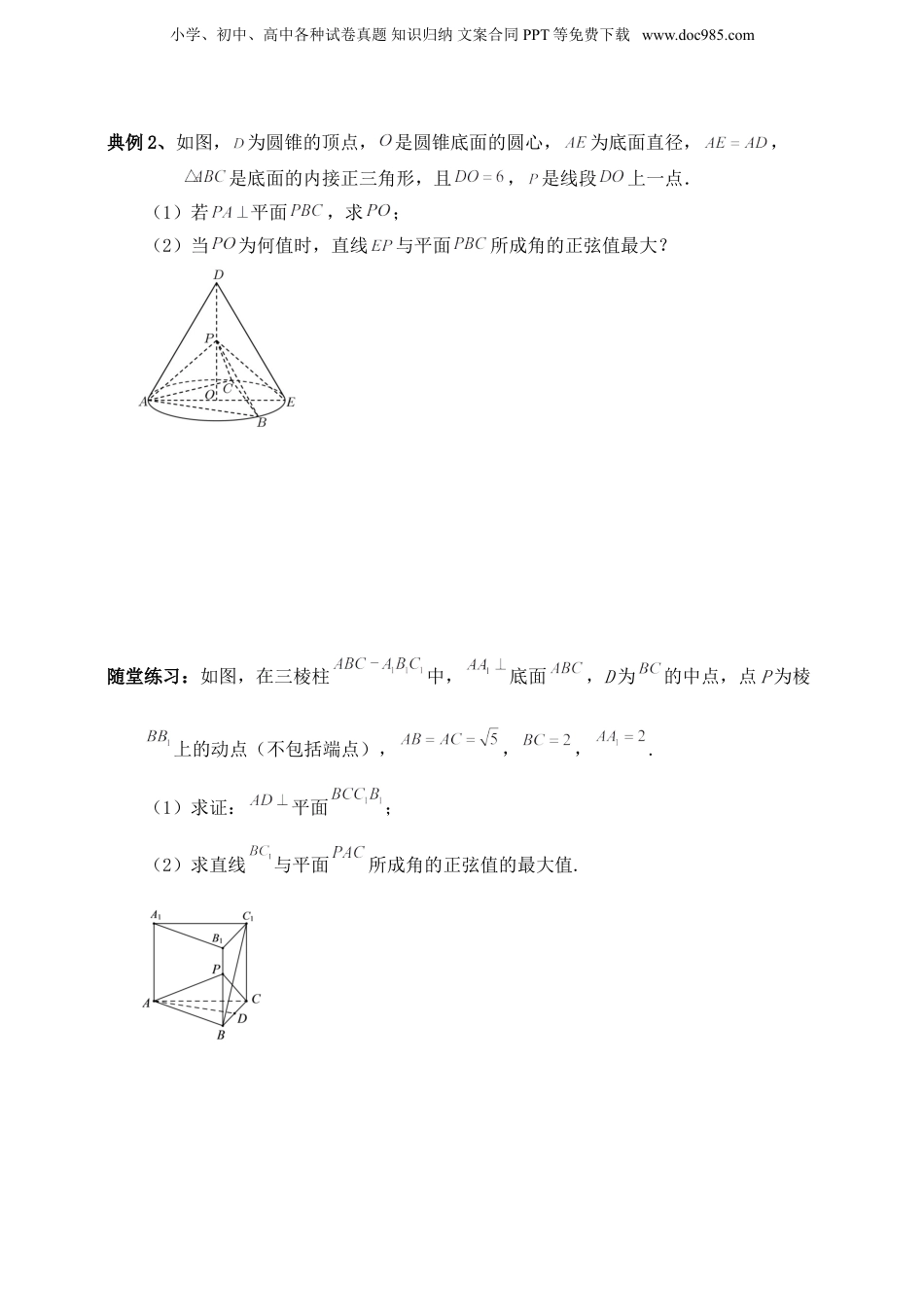
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com空间向量和立体几何高考复习专题八知识点一证明线面垂直,求线面角,面面垂直证线面垂直,线面角的向量求法典例1、已知，如图四棱锥中，底面ABCD为菱形，，，平面ABCD，E，M分别是BC，PD中点，点F是棱PC上的动点．（1）证明：平面PAD；（2）请确定F点的位置，使得直线AF与平面PCD所成的角取最大值．随堂练习：已知正方体和平面，直线平面，直线平面.（1）证明：平面平面；（2）点为线段上的动点，求直线与平面所成角的最大值.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com典例2、如图，为圆锥的顶点，是圆锥底面的圆心，为底面直径，，是底面的内接正三角形，且，是线段上一点．（1）若平面，求；（2）当为何值时，直线与平面所成角的正弦值最大？随堂练习：如图，在三棱柱中，底面，D为的中点，点P为棱上的动点（不包括端点），，，.（1）求证：平面；（2）求直线与平面所成角的正弦值的最大值.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com典例3、在四棱锥中，平面，底面是直角梯形，其中，，，为棱上的点，且．（1）求证：平面；（2）若二面角的平面角的正切值为，求的长；（3）在（2）的条件下，若为线段上一点，求与面所成角为，求的最大值．随堂练习：如图，在四棱锥中，底面是梯形，，，，.（1）证明：平面；（2）若，当四棱锥的体积最大时，求直线与平面所成角的正弦值.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com知识点一锥体体积的有关计算,证明面面垂直典例4、边长为1的正方形中，点M，N分别是DC，BC的中点，现将，分别沿AN，AM折起，使得B，D两点重合于点P，连接PC，得到四棱锥.（1）证明：平面平面；（2）求四棱锥的体积.随堂练习：如图，在四棱锥中，底面ABCD，，，，，．（1）证明：平面PCD⊥平面PBC；（2）若，求三棱锥的体积．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com典例5、如图，在三棱柱中，，，，点D，E，F分别为线段BC，，的中点，且.（1）证明：平面平面ABC；（2）若，求三棱锥的体积.随堂练习：如图，三棱柱中，侧面为矩形，是边长为2的菱形，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com，．（1）证明：平面平面；（2）若，求三棱柱的体积．典例6、如图，已知在四棱锥中，，，，，E，F分别为棱PB，PA的中点．（1）求证：平面平面EFDC；（2）若直线PC与平面PAD所成的角为45°，求四棱锥的体积．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com随堂练习：如图，四棱锥中，侧面为等边三角形且垂直于底面，，，是的中点.（1）求证：平面平面；（2）点在棱上，满足且三棱锥的体积为，求的值.空间向量和立体几何高考复习专题八答案典例1、答案：（1）证明见解析（2）解：（1）证明：在正方形中有，，，，又因为，所以平面，而平面，所以平面平面.（2）连接MN,由题意可得，，，由，所以为直角三角形，即小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com，设点到平面的距离为，由得，，即，得，即四棱锥的体积为随堂练习：答案：（1）证明见解析（2）解：（1）连接，因为，所以,又因为，，所以，即,又因为底面ABCD，底面ABCD，所以BC，又因为平面PCD，，所以平面PCD,又因为平面PBC，所以平面PCD⊥平面PBC.（2）在直角三角形中，在直角三角形中，所以，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以，所以.典例2、答案：（1）证明见解析（2）解：（1）如图，取AC的中点O，连接OD，，因为，，所以为等边三角形，所以.又因为，点O，D分别为线段AC，BC的中点，所以，所以，因为，，平面，所以平面， 平面，则，又因为，平面ABC，所以平面ABC，又因为平面，所以平面平面ABC.（2）如图，过B作于点G，由（1）得平面平面ABC，且平面平面，平面，所以平面，在直角ABC中，，，，所以，由，又因为点D为线段BC的中点，所以点D到平面的距离h为点B到平面的...