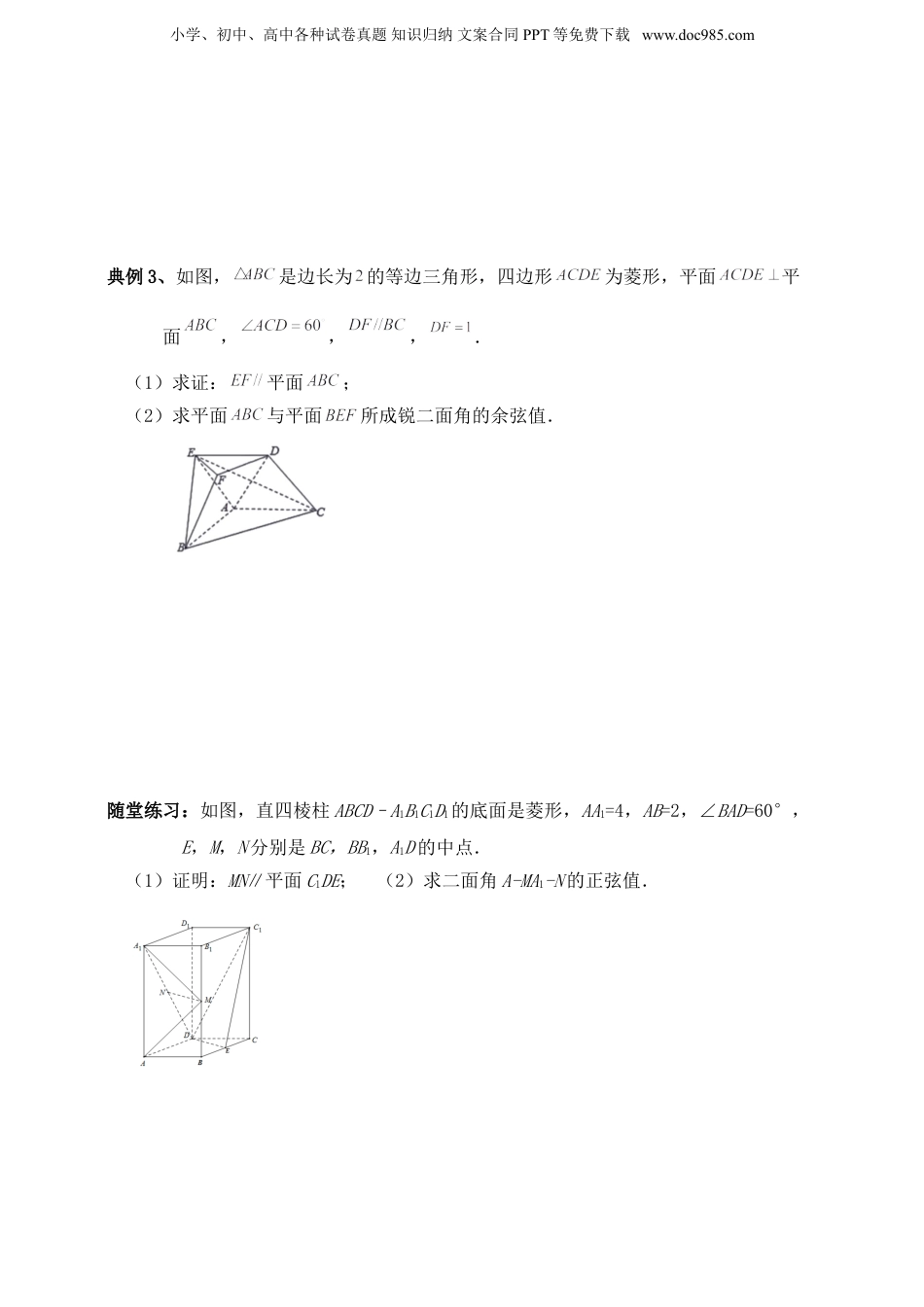
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com空间向量和立体几何高考复习专题十四知识点一证明线面平行,面面角的向量求法典例1、如图，是圆的直径，点是圆上异于的点，直线平面，分别是，的中点.（1）记平面与平面的交线为，求证：直线平面；（2）若，点是的中点，求二面角的正弦值.随堂练习：如图，三棱柱中侧棱与底面垂直，且，，，M，N，P，D分别为，BC，，的中点.（1）求证：面；（2）求平面PMN与平面所成锐二面角的余弦值.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com典例2、如图所示的几何体中，，，都是等腰直角三角形，，且平面平面，平面平面．（1）求证：平面；（2）求平面与平面夹角的余弦值．随堂练习：如图，在四棱锥中，平面，，为等边三角形，．（1）求证：平面，且平面．（2）已知，，求平面与平面所成锐二面角的余弦值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com典例3、如图，是边长为的等边三角形，四边形为菱形，平面平面，，，．（1）求证：平面；（2）求平面与平面所成锐二面角的余弦值．随堂练习：如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E，M，N分别是BC，BB1，A1D的中点．（1）证明：MN∥平面C1DE；（2）求二面角A-MA1-N的正弦值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com知识点二证明线面垂直,线面垂直证明线线垂直,线面角的向量求法典例4、如图，在四棱锥中，底面是正方形，平面，，点是的中点.（1）求证：；（2）求直线与平面所成角的正弦值.随堂练习：如图，在直角中，PO⊥OA，PO=2OA，将绕边PO旋转到的位置，使，得到圆锥的一部分，点C为的中点．（1）求证：；（2）设直线PC与平面PAB所成的角为，求．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com典例5、在四棱锥中，底面ABCD为直角梯形，，，，E为的中点，点P在平面内的投影F恰好在直线上．（1）证明：．（2）求直线与平面所成角的正弦值．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com随堂练习：如图，在中，，，为的中点，，.现将沿翻折至，得四棱锥.（1）证明：；（2）若，求直线与平面所成角的正切值典例6、如图，在七面体中，四边形是菱形，其中，，，是等边三角形，且.（1）证明：；（2）求直线与平面所成角的正弦值.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com随堂练习：如图，在四棱锥中，平面，，且，，，点在上．（1）求证：；（2）若二面角的大小为，求与平面所成角的正弦值．空间向量和立体几何高考复习专题十四答案典例1、答案：（1）证明见解析（2）解：（1）因为分别是的中点所以，又因为平面，平面所以平面又平面，平面与平面的交线为，所以，而平面，平面，所以平面小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（2）如图，因为是圆的直径，点是的中点，所以，因为直线平面所以所以以为原点，直线，，分别为轴，轴，轴，建立空间直角坐标系，则，，所以，设平面的法向量，则，即令，则得因为直线平面所以为平面的法向量所以所以二面角的正弦值为随堂练习：答案：（1）证明见解析（2）解：（1）解法一：以点A为坐标原点，AB､AC､所在直线分别为x､y､z轴建立空间直角坐标系，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com则，，，，.取向量为平面的一个法向量，，∴，∴.又 平面，∴平面.解法二： P，D分别为，的中点，∴，且平面，平面，∴平面， D，N分别为，BC的中点，∴，且平面，平面，∴平面，又，∴平面平面，又 平面PDN，∴平面.以点A为坐标原点，AB､AC､所在直线分别为x，y，z轴建立空间直角坐标系，则，，，，.∴，,取向量为平面的一个法向量，设平面PMN的法向量为，则，即，令，则，，则，∴，由图示可知平面PMN与平面的夹角为锐角，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com∴平面PMN与平面所成锐二面角的余弦值...