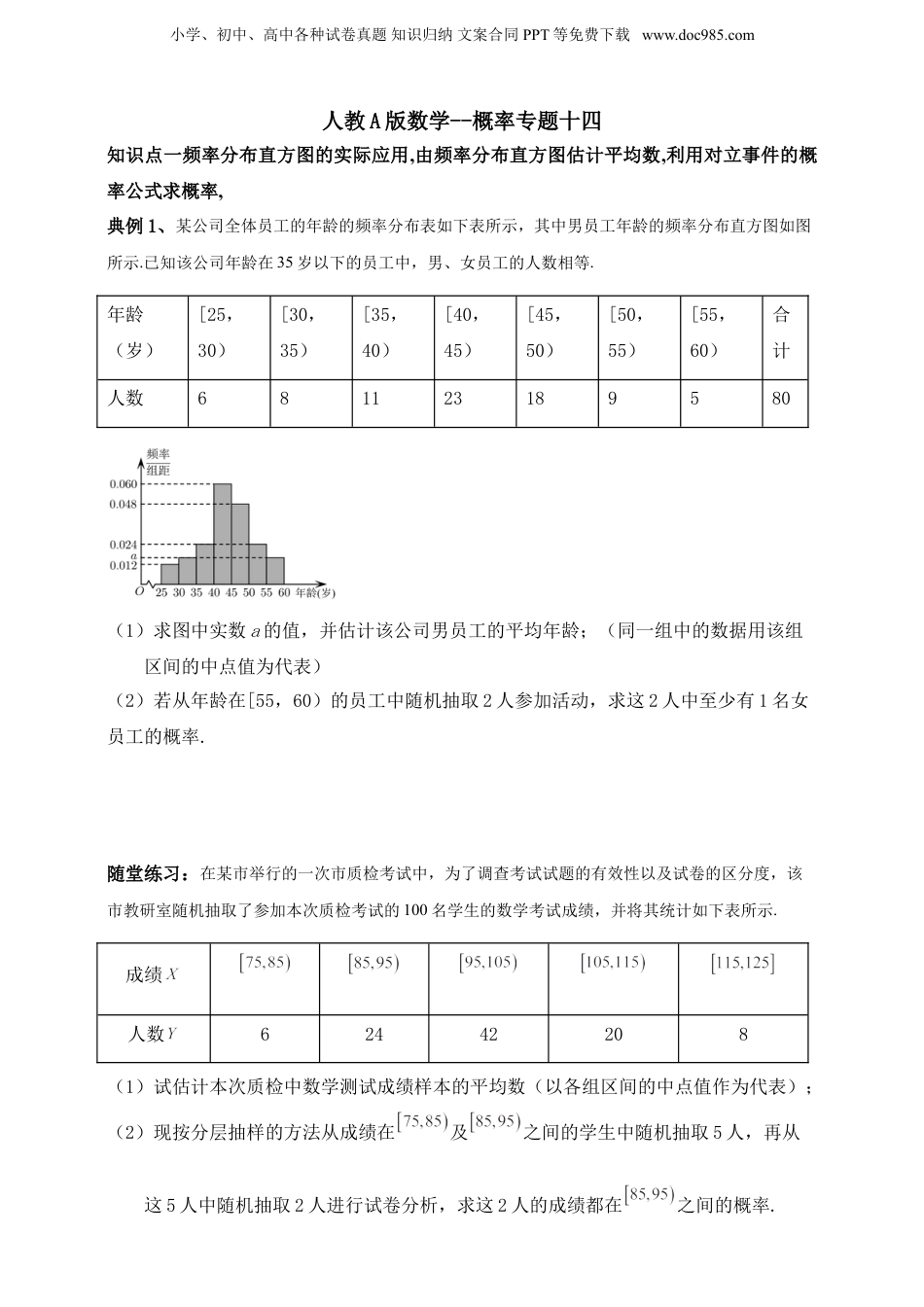
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com人教A版数学--概率专题十四知识点一频率分布直方图的实际应用,由频率分布直方图估计平均数,利用对立事件的概率公式求概率,典例1、某公司全体员工的年龄的频率分布表如下表所示，其中男员工年龄的频率分布直方图如图所示.已知该公司年龄在35岁以下的员工中，男、女员工的人数相等.年龄（岁）[25，30）[30，35）[35，40）[40，45）[45，50）[50，55）[55，60）合计人数681123189580（1）求图中实数a的值，并估计该公司男员工的平均年龄；（同一组中的数据用该组区间的中点值为代表）（2）若从年龄在[55，60）的员工中随机抽取2人参加活动，求这2人中至少有1名女员工的概率.随堂练习：在某市举行的一次市质检考试中，为了调查考试试题的有效性以及试卷的区分度，该市教研室随机抽取了参加本次质检考试的100名学生的数学考试成绩，并将其统计如下表所示.成绩人数62442208（1）试估计本次质检中数学测试成绩样本的平均数（以各组区间的中点值作为代表）；（2）现按分层抽样的方法从成绩在及之间的学生中随机抽取5人，再从这5人中随机抽取2人进行试卷分析，求这2人的成绩都在之间的概率.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com典例2、2022年，是中国共产主义青年团成立100周年，为引导和带动青少年重温共青团百年光辉历程，某校组织全体学生参加共青团百年历史知识竞赛，现从中随机抽取了100名学生的成绩组成样本，并将得分分成以下6组：[40，50）、[50，60）、[60，70）、、[90，100]，统计结果如图所示：（1）试估计这100名学生得分的平均数（同一组中的数据用该组区间中点值代表）；（2）试估计这100名学生得分的中位数（结果保留两位小数）；（3）现在按分层抽样的方法在[80，90）和[90，100]两组中抽取5人，再从这5人中随机抽取2人参加这次竞赛的交流会，试求两组各有一人被抽取的概率.随堂练习：某校组织学生观看“太空授课”，激发了学生的学习热情.学校组织1000名学生进行科学探索知识竞赛，成绩分成5组：，，，，，得到如图所示的频率分布直方图.若图中未知的数据a，b，c成等差数列，成绩落在区间内的人数为400.（1）求出直方图中a，b，c的值；（2）估计中位数（精确到0.1）和平均数（同一组中的数据用该组区间的中点值代小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com替）；（3）若从得分在区间内的学生中抽取2人编号为A，B，从得分在区间内的学生中抽取6人编号为1，2，3，4，5，6，组成帮助小组，从1，2，3，4，5，6中选3个人帮助A，余下的3个人帮助B，求事件“1，2帮助A”的概率.典例3、《中共中央国务院关于深入打好污染防治攻坚战的意见》提出“构建智慧高效的生态环境管理信息化体系”，下一步，需加快推进5G、物联网、大数据、云计算等新信息技术在生态环境保护领域的建设与应用，实现生态环境管理信息化、数字化、智能化．某科技公司开发出一款生态环保产品，已知该环保产品每售出1件预计利润为0.4万元，当月未售出的环保产品，每件亏损0.2万元．根据市场调研，该环保产品的市场月需求量在内取值，将月需求量区间平均分成5组，画出频率分布直方图如下．（1）请根据频率分布直方图，估计该环保产品的市场月需求量的平均值和方差．（2）若该环保产品的月产量为185件，x（单位：件，，）表示该产品一个月内的市场需求量，y（单位：万元）表示该公司生产该环保产品的月利润．①将y表示为x的函数；②以频率估计概率，标准差s精确到1，根据频率分布直方图估计且y不少于68万元的概率．随堂练习：新冠肺炎疫情期间，某地为了了解本地居民对当地防疫工作的满意度，从本小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com地居民中随机抽取若干居民进行评分（满分为100分），根据调查数据制成如下频率分布直方图，已知评分在的居民有660人.（1）求频率分布直方图中的值及所调查的总人数；（2）从频率分布直方图中，估计本次评测分数的中位数和平均数（精确到0.1）；（3）为了今后更好地完成当地的防疫工作，政府部...