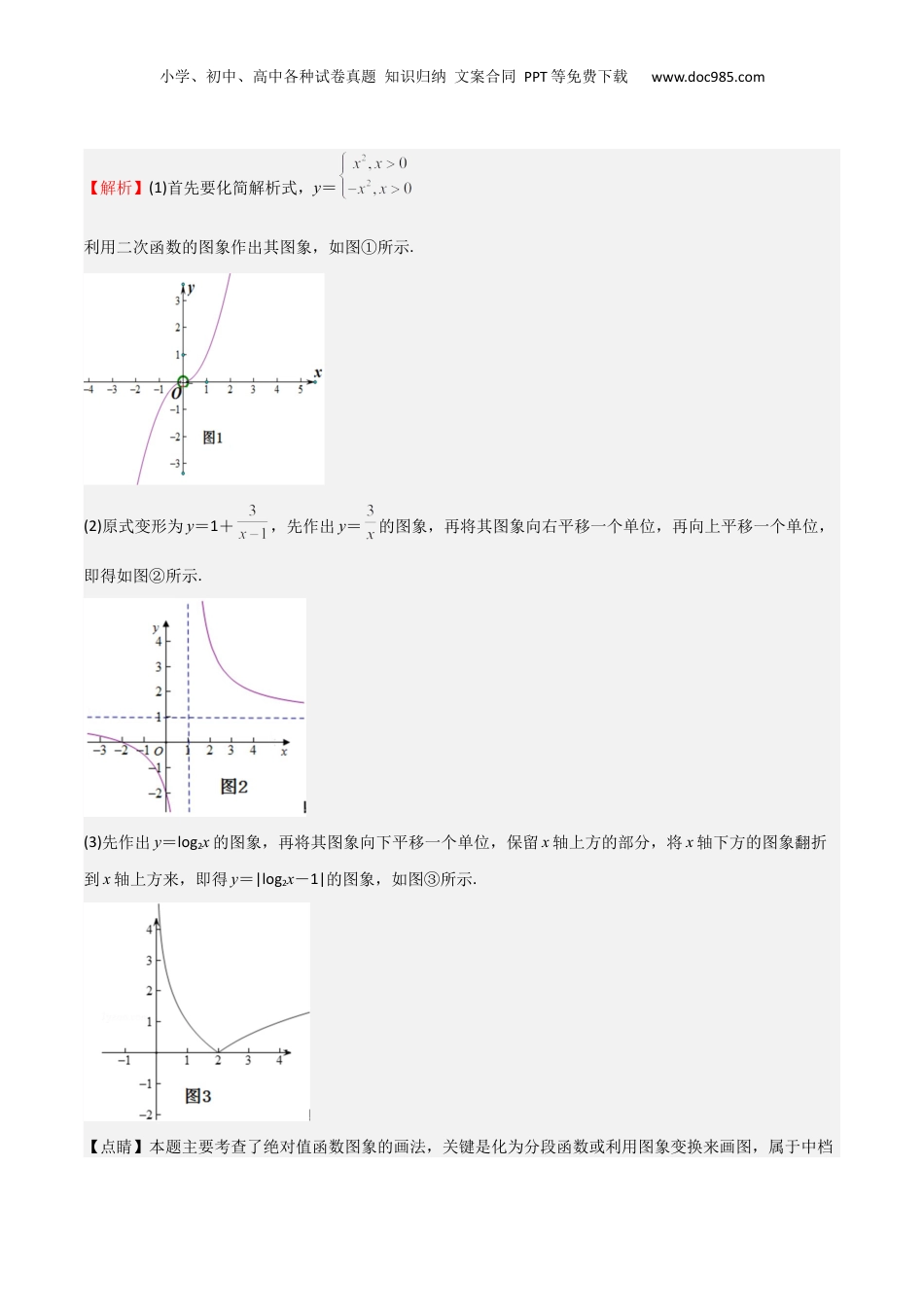
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题09函数的图像函数的零点（八大题型+模拟精练）目录：01画函数的变换图像02识别函数的图像03函数图像变换的应用04求函数的零点及个数05二分法求函数的零点06根据函数的零点求参数07函数零点的其他应用08补函数的应用（一）：几类不同增长的函数模型、函数的实际应用01画函数的变换图像1．（2024高三·全国·专题练习）作出下列函数的图象：(1)；(2)；(3)y＝|log2x－1|；【答案】（1）见解析；（2）见解析；（3）见解析.【分析】(1)去绝对值化简成分段函数，画出图象即可．(2)原式变形为y＝1＋，先作出y＝的图象，再结合图象变换，即可得出结论．(3)先作出y＝log2x的图象，结合图象变换，即可得出结论．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【解析】(1)首先要化简解析式，y＝利用二次函数的图象作出其图象，如图①所示.(2)原式变形为y＝1＋，先作出y＝的图象，再将其图象向右平移一个单位，再向上平移一个单位，即得如图②所示.(3)先作出y＝log2x的图象，再将其图象向下平移一个单位，保留x轴上方的部分，将x轴下方的图象翻折到x轴上方来，即得y＝|log2x－1|的图象，如图③所示.【点睛】本题主要考查了绝对值函数图象的画法，关键是化为分段函数或利用图象变换来画图，属于中档小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com题．02识别函数的图像2．（2023·湖南岳阳·模拟预测）函数的图象为（）A．B．C．D．【答案】D【分析】利用特殊点法与图象平移即可得解.【解析】因为，所以当时，，故排除ABC，又的图象可由函数的图象向右平移一个单位得到，则D正确.故选：D.3．（2024·湖北·模拟预测）函数的图象大致为（）A．B．C．D．【答案】A【分析】根据时的单调性可排除BC；再由奇偶性可排除D.小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com【解析】，因为当时，都为增函数，所以，在上单调递增，故B，C错误；又因为，所以不是奇函数，即图象不关于原点对称，故D错误.故选：A4．（2024·宁夏固原·一模）已知函数的部分图像如图所示，则的解析式可能为（）A．B．C．D．【答案】A【分析】利用在上的值排除B，利用奇偶性排除排除C，利用在上的单调性排除D，从而得解.【解析】对于B，当时，，易知，，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com则，不满足图象，故B错误；对于C，，定义域为，又，则的图象关于轴对称，故C错误；对于D，当时，，由反比例函数的性质可知，在上单调递减，故D错误；检验选项A，满足图中性质，故A正确.故选：A.03函数图像变换的应用5．（2024·四川南充·二模）已知函数，则函数的图象（）A．关于点对称B．关于点对称C．关于点对称D．关于点对称【答案】A【分析】首先判断函数为奇函数，再根据函数平移规则判断即可.【解析】函数的定义域为，又，所以为奇函数，则函数的图象关于原点对称，又的图象是由的图象向右平移个单位，再向上平移个单位得到，小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com所以函数的图象关于点对称.故选：A6．（22-23高二上·河南·阶段练习）直线过函数图象的对称中心，则的最小值为（）A．9B．8C．6D．5【答案】A【分析】先利用函数图象平移与奇函数的性质求得的对称中心，从而得到，再利用基本不等式“1”的妙用即可得解.【解析】函数的图象，可由的图象向右平移1个单位，再向上2个单位得到，又的定义域为，，所以是奇函数，则其对称中心为，故的对称中心为，所以，即，所以，当且仅当，即时,等号成立，所以的最小值为.故选：A.7．（2022高三·全国·专题练习）已知二次函数的图象的顶点坐标是，且截轴所得线段的长度小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com是4，将函数的图象向右平移2个单位长度，得到抛物线，则抛物线与轴的交点是（）A．B．C．D．【答案】B【分析】利用二次函数的性质，结合待定系数法求得，再利用平移的特征求得，从而得解.【解析】因为...