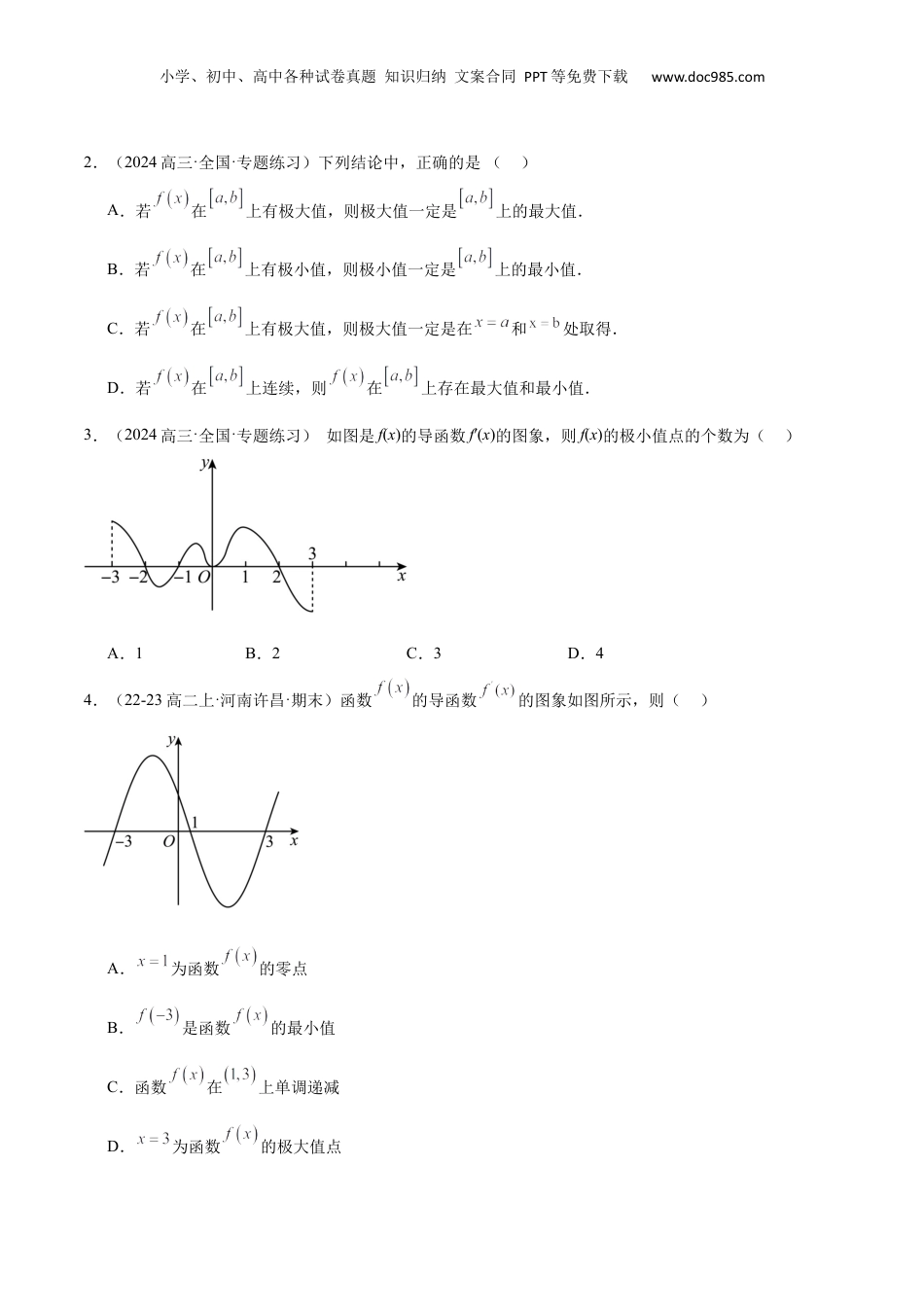
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题15导数与函数的极值、最值（十一大题型+模拟精练）目录：01函数极值的辨析02求已知函数的极值03根据极值求参数04函数（导函数）图像与极值的关系05由导数求函数的最值06已知函数最值求参数07根据极值点求参数08由导数求函数的最大值（含参）09恒成立问题10零点问题11导数的综合应用01函数极值的辨析1．（2024高三·全国·专题练习）下列函数中，存在极值的函数为（）A．B．C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2．（2024高三·全国·专题练习）下列结论中，正确的是（）A．若在上有极大值，则极大值一定是上的最大值．B．若在上有极小值，则极小值一定是上的最小值．C．若在上有极大值，则极大值一定是在和处取得．D．若在上连续，则在上存在最大值和最小值．3．（2024高三·全国·专题练习）如图是f(x)的导函数f′(x)的图象，则f(x)的极小值点的个数为（）A．1B．2C．3D．44．（22-23高二上·河南许昌·期末）函数的导函数的图象如图所示，则（）A．为函数的零点B．是函数的最小值C．函数在上单调递减D．为函数的极大值点小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com02求已知函数的极值5．（2024·黑龙江·模拟预测）已知函数．(1)当时，求在点处的切线方程；(2)讨论的单调性，并求出的极小值．6．（23-24高二下·湖南·期中）已知函数为奇函数．(1)求的值；(2)当时，求的单调区间和极值．03根据极值求参数7．（22-23高二下·北京·期中）若函数恰好有两个极值，则实数a的取值范围是（）A．B．C．D．8．（2023·贵州遵义·三模）已知函数在处取得极值0，则（）A．-1B．0C．1D．29．（21-22高三下·广西·阶段练习）已知函数在其定义域的一个子区间上有极值，则实数a的取值范围是（）A．B．C．D．04函数（导函数）图像与极值的关系10．（23-24高二下·江西赣州·阶段练习）已知函数的导函数的图象如图所示，则下列说法错误的是（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．函数在上单调递增B．函数至少有2个极值点C．函数在上单调递减D．函数在处取得极大值11．（23-24高二下·四川广元·期中）函数的导函数的图象如图所示，则下列判断中正确的是（）A．在上单调递减B．在上单调递减C．在上存在极小值点D．在上有最大值05由导数求函数的最值12．（23-24高二下·四川成都·期中）已知函数，，若，则的最小值为（）A．B．C．D．13．（2024·江西鹰潭·二模）已知函数，，则下列命题不正确的是（）A．有且只有一个极值点B．在上单调递增小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comC．存在实数，使得D．有最小值14．（23-24高二下·北京海淀·期中）关于函数，下列结论错误的是（）A．的解集是B．是极小值，是极大值C．没有最小值，也没有最大值D．有最大值，没有最小值06已知函数最值求参数15．（23-24高二下·四川内江·阶段练习）已知在区间上有最小值，则实数的取值范围是（）A．B．C．D．16．（23-24高二下·四川遂宁·阶段练习）若函数在区间上存在最值，则的取值范围是（）A．B．C．D．或17．（23-24高二下·湖北武汉·阶段练习）设函数，若，且的最小值为，则的值为（）A．B．C．D．07根据极值点求参数18．（23-24高二上·江苏盐城·期末）已知函数的导函数，若是函数的极大值点，则实数的取值范围是（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．19．（23-24高三上·河南南阳·期末）若函数有两个不同的极值点，则实数a的取值范围为（）A．B．C．D．20．（22-23高三下·江西赣州·阶段练习）已知函数存在两个极值点，则以下结论正确的为（）A．B．C．若，则D．08由导数求函数的最大值（含参）21．（23-24高二下·海南省直辖县级单位·阶段练习）已知函数，其中．(1)当时，求的单调区间；(2)当时，函数在区间上的最小值．22．（2024·山西吕梁·二模）已知函数.(1)当时，求的单调区间和极值；(2)求在区间...