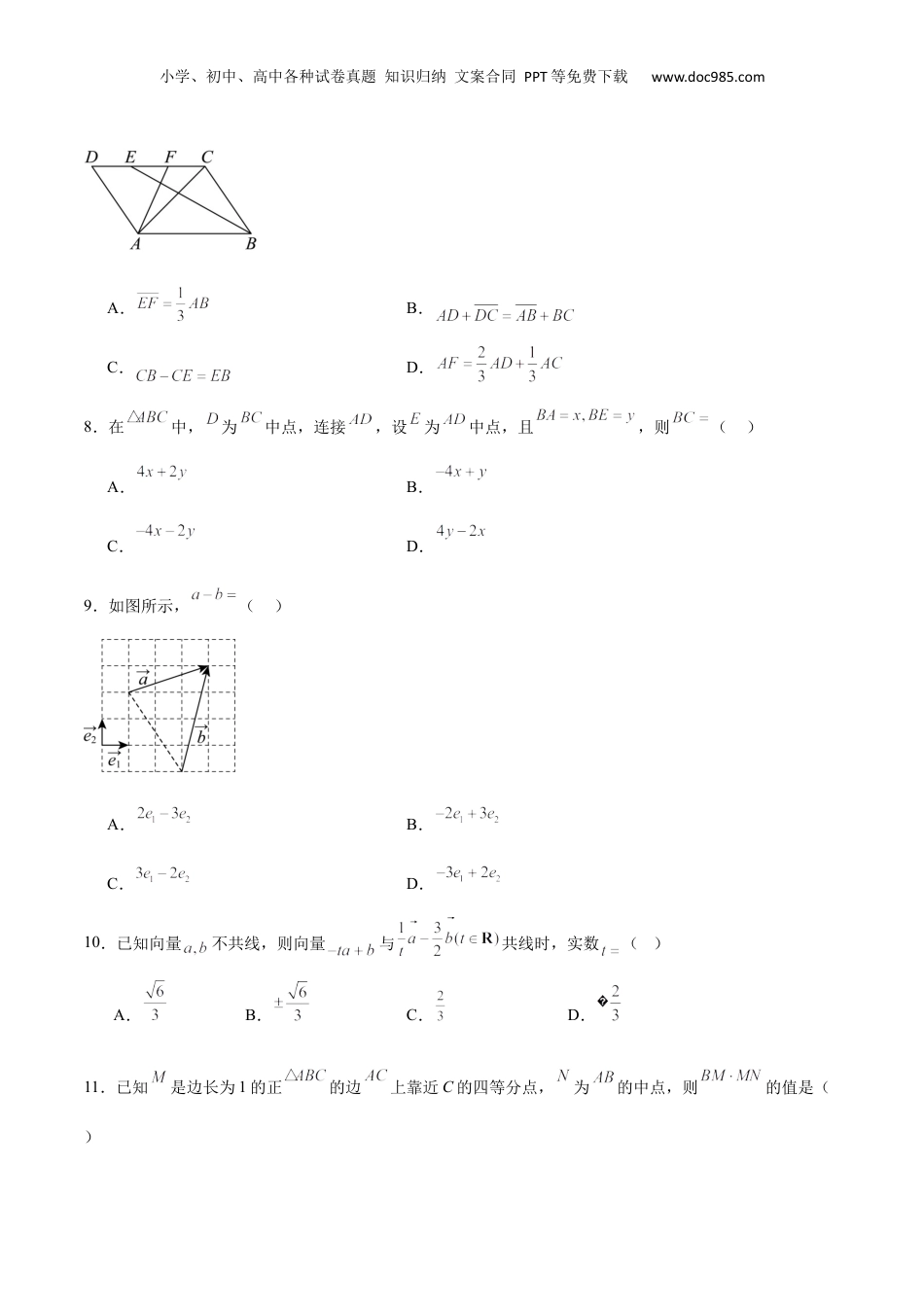
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题16平面向量及其应用（六大题型+模拟精练）目录：01平面向量的有关概念02平面向量的线性运算03平面向量的数量积04平面向量的基本定理与坐标表示05平面向量的综合应用06三角形的“心”的向量表示01平面向量的有关概念1．下列说法错误的是（）．A．零向量没有方向B．两个相等的向量若起点相同，则终点必相同C．只有零向量的模等于0D．向量与的长度相等2．若向量与为非零向量，下列命题中正确的是（）A．若，则B．C．若非零向量，则与的方向相同小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comD．若，则3．与向量平行的所有单位向量为（）A．B．C．D．或4．已知两个单位向量，的夹角是，则.02平面向量的线性运算5．在中，是的中点，在上，且，则（）A．B．C．D．6．如图所示，在中，为BC边上的三等分点，若，，为AD中点，则（）A．B．C．D．7．如图，在平行四边形中，E、F分别是边上的两个三等分点，则下列选项错误的是（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．8．在中，为中点，连接，设为中点，且，则（）A．B．C．D．9．如图所示，（）A．B．C．D．10．已知向量不共线，则向量与共线时，实数（）A．B．C．D．11．已知是边长为1的正的边上靠近C的四等分点，为的中点，则的值是（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．12．在中，且，则错误的选项为（）A．B．C．D．03平面向量的数量积13．在中，内角所对的边分别为，是的中点，，则．14．在中，，P是线段AD上的动点（与端点不重合），设，则的最小值是.15．已知向量满足，，则（）A．－2B．C．D．616．已知平面向量，均为单位向量，若，则向量，的夹角（）A．B．C．D．17．若向量与的夹角为锐角，则实数的取值范围是.18．已知是单位向量，且在上的投影向量为，则与的夹角为（）A．B．C．D．19．已知向量，，，若与的夹角为，且⊥，则实数的值为（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．20．在矩形中，，，E为的中点，F为的中点，Q为边上的动点（包括端点），则的取值范围为．21．已知是圆O：的直径，M，N是圆O上两点，且，则的最小值为（）A．0B．-2C．-4D．22．在平行四边形中，，点为该平行四边形所在平面内的任意一点，则的最小值为（）A．6B．8C．10D．1204平面向量的基本定理与坐标表示23．设、是不共线的两个非零向量，则下列四组向量不能作为基底的是（）A．和B．与C．与D．与24．在中，内角A，B，C所对的边分别为，，.向量，若，则角的大小为（）A．B．C．D．25．已知向量，的夹角为，，，在中，，，，则（）A．2B．C．D．6小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com26．已知向量，若不超过，则的取值范围为（）A．B．C．D．27．如图，在等腰梯形中，，则.28．如图，点是的重心，点是边上一点，且，，则（）A．B．C．D．29．如图，边长为2的等边三角形的外接圆为圆O，P为圆O上任一点，若，则的最大值为（）A．B．2C．D．130．如图，四边形是边长为1的正方形，延长CD至E，使得．动点P从点A出发，沿正方形的边按逆时针方向运动一周回到A点，，则的取值范围为．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com31．已知菱形边长为1，且为线段的中点，若在线段上，且，则，点为线段上的动点，过点作的平行线交边于点，过点做的垂线交边于点，则的最小值为.05平面向量的综合应用32．在中，，，则的形状为（）A．等腰直角三角形B．三边均不相等的三角形C．等边三角形D．等腰（非直角）三角形33．已知圆锥的底面半径为2，点P为底面圆周上任意一点，点Q为侧面（异于顶点和底面圆周）上任意一点，则的取值范围为（）A．B．C．D．34．已知圆的半径为1，过圆外一点作一条切线与圆相切于点，，为圆上一个动点，则的取值范围为（）A．B．C．D．35．如图所示，O点在内部，分别是边的中点，且有，则的面积与的面积的...