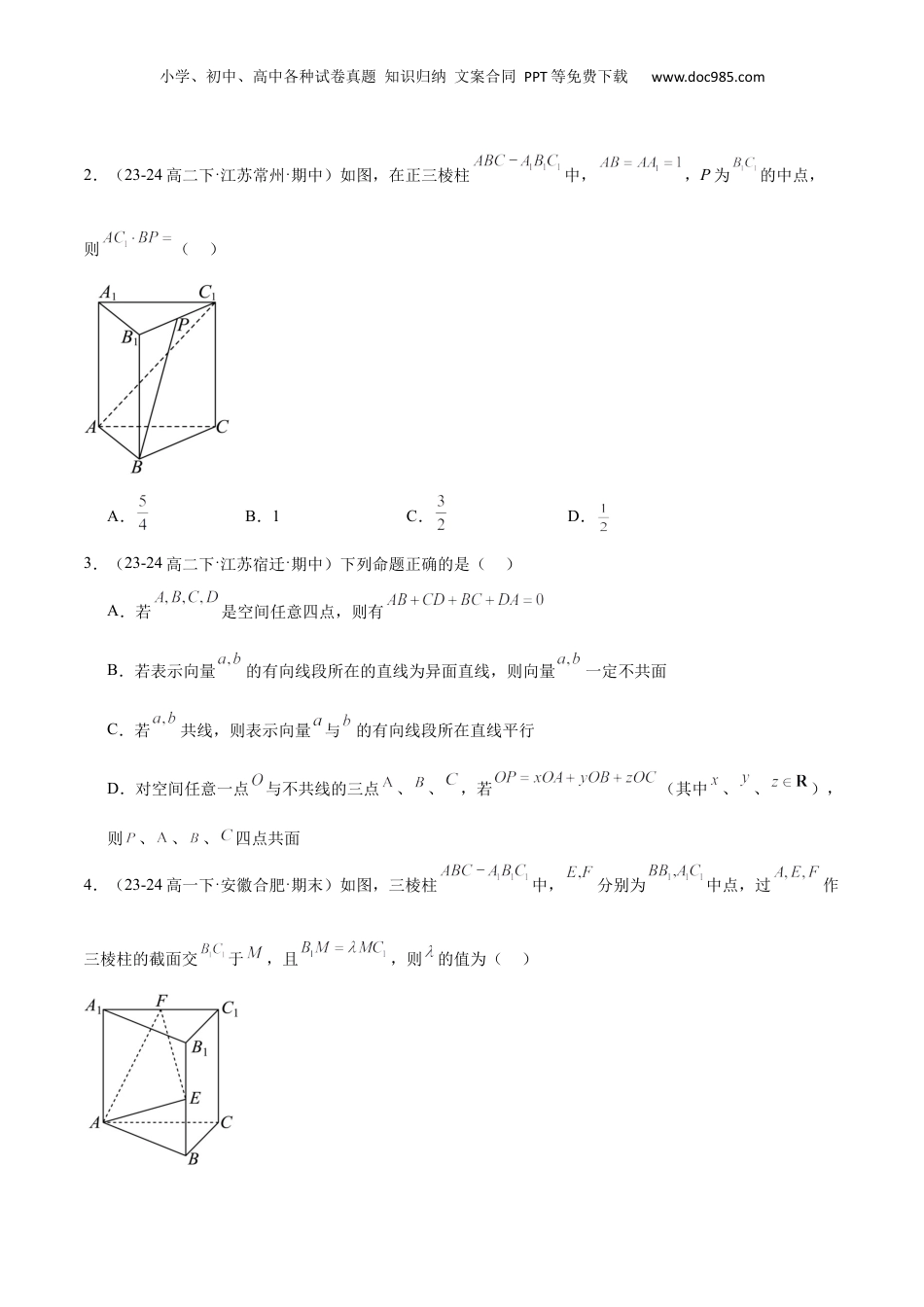
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题20空间向量与立体几何（八大题型+模拟精练）目录：01空间向量的线性运算02空间向量的数量积03空间向量的基本定理04空间向量的坐标表示05利用空间向量判断位置关系06利用空间向量求角度07利用空间向量求距离08空间向量与立体几何解答题01空间向量的线性运算1．（2024高三·全国·专题练习）如图，在空间四边形中，，分别是，的中点，则（）A．B．C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com2．（23-24高二下·江苏常州·期中）如图，在正三棱柱中，，P为的中点，则（）A．B．1C．D．3．（23-24高二下·江苏宿迁·期中）下列命题正确的是（）A．若是空间任意四点，则有B．若表示向量的有向线段所在的直线为异面直线，则向量一定不共面C．若共线，则表示向量与的有向线段所在直线平行D．对空间任意一点与不共线的三点、、，若（其中、、），则、、、四点共面4．（23-24高一下·安徽合肥·期末）如图，三棱柱中，分别为中点，过作三棱柱的截面交于，且，则的值为（）小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.comA．B．C．D．102空间向量的数量积5．（23-24高二下·湖北·期末）空间向量在上的投影向量为（）A．B．C．D．6．（23-24高二下·福建龙岩·期中）如图，在斜三棱柱中，，，，则（）A．48B．32C．D．7．（23-24高二下·福建漳州·期末）正方体的棱长为，是正方体外接球的直径，为正方体表面上的动点，则的取值范围是（）A．B．C．D．8．（2024·河南新乡·二模）已知圆锥的底面半径为，高为1，其中为底面圆心，是底面圆的一条直径，若点在圆锥的侧面上运动，则的最小值为（）A．B．C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com03空间向量的基本定理9．（24-25高二上·上海·课后作业）如图，在四面体OABC中，，，，若，且∥平面ABC，则实数（）A．B．C．D．10．（22-23高二上·江西南昌·期末）已知点在确定的平面内，是平面外任意一点，实数满足，则的最小值为（）A．B．C．1D．211．（23-24高二下·江苏淮安·阶段练习）以等腰直角三角形斜边上高为折痕，把和折成的二面角.若，，则最小值为（）A．B．C．D．04空间向量的坐标表示12．（2023·河南·模拟预测）已知空间向量，若共面，则实数（）A．1B．2C．3D．4小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com13．（23-24高二下·福建莆田·期末）在三棱锥中，，，两两垂直，且.若为该三棱锥外接球上的一点，则的最大值为（）A．2B．4C．D．14．（23-24高二下·福建·期中）在棱长为2的正方体中，若点P是棱上一点(含顶点)，则满足的点P的个数为（）A．8B．12C．18D．2405利用空间向量判断位置关系15．（23-24高二下·甘肃·期中）已知平面外的直线l的方向向量为，平面的一个法向量为，则（）A．l与斜交B．C．D．16．（23-24高三下·湖南衡阳·阶段练习）空间四边形中分别为的点（不含端点）.四边形为平面四边形且其法向量为.下列论述错误项为（）A．，则//平面B．，则平面C．，则四边形为矩形.D．，则四边形为矩形.17．（23-24高二下·江苏扬州·阶段练习）正方体的棱长为1，动点在线段上，动点小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com在平面上，且平面，线段长度的取值范围是（）A．B．C．D．18．（2024·宁夏吴忠·模拟预测）在正方体中，点为线段上的动点，直线为平面与平面的交线，现有如下说法①不存在点，使得平面②存在点，使得平面③当点不是的中点时，都有平面④当点不是的中点时，都有平面其中正确的说法有（）A．①③B．③④C．②③D．①④06利用空间向量求角度19．（23-24高二下·福建厦门·期末）在四面体中，，，，，则与所成角的余弦值为（）A．B．C．D．小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com20．（2024·陕西·模拟预测）在平行六面体中，已知，，则下列选项中错误的一项是（）A．直线与BD所成的角为90°B．线段的长度...