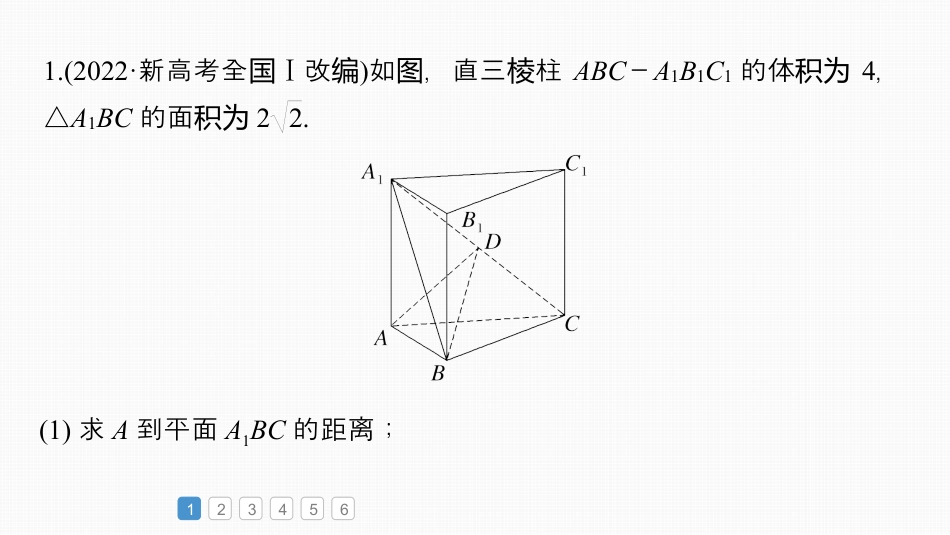
必刷大题14空间向量与立体几何第七章立体几何与空间向量1234561.(2022·新高考全国Ⅰ改编)如，直三柱图棱ABC－A1B1C1的体积为4，△A1BC的面积为22.(1)求A到平面A1BC的距离；123456点设A到平面A1BC的距离为h，因直三柱为棱ABC－A1B1C1的体积为4，所以＝13S△ABC·AA11AABCV1111433ABCABCV，又△A1BC的面积为22，1113AABCABCVSh△＝13×22h＝43，所以h＝2，即点A到平面A1BC的距离为2.123456(2)设D为A1C的中点，AA1＝AB，平面A1BC⊥平面ABB1A1，求平面ABD平面与BCD角的正弦夹值.123456取A1B的中点E，接连AE，则AE⊥A1B.因平面为A1BC⊥平面ABB1A1，平面A1BC∩平面ABB1A1＝A1B，AE⊂平面ABB1A1，所以AE⊥平面A1BC，又BC⊂平面A1BC，所以AE⊥BC.又AA1⊥平面ABC，BC⊂平面ABC，所以AA1⊥BC.123456因为AA1∩AE＝A，AA1，AE⊂平面ABB1A1，所以BC⊥平面ABB1A1，又AB⊂平面ABB1A1，所以BC⊥AB.以B坐原点，分以为标别BC→，BA→，BB1—→的方向为x，y，z的正方向，建立如所示轴图的空直角坐系，间标由(1)知，AE＝2，所以AA1＝AB＝2，A1B＝22.123456因为△A1BC的面积为22，所以22＝12·A1B·BC，所以BC＝2，则BD→＝(1,1,1)，BA→＝(0,2,0).所以A(0,2,0)，B(0,0,0)，C(2,0,0)，A1(0，2,2)，D(1,1,1)，E(0,1,1)，平面设ABD的法向量为n＝(x，y，z)，则n·BD→＝0，n·BA→＝0，即x＋y＋z＝0，2y＝0，123456又平面BDC的一法向量个为AE→＝(0，－1，1)，令x＝1，得n＝(1,0，－1).所以cos〈AE→，n〉＝AE→·n|AE→|·|n|＝－12×2＝－12.平面设ABD平面与BCD的角夹为θ，则sinθ＝1－cos2〈AE→，n〉＝32，所以平面ABD平面与BCD角的正弦夹值为32.2.如，四图棱锥P－ABCD的底面正方形，为PA⊥平面ABCD，M是PC的中点，PA＝AB.123456(1)求：证AM⊥平面PBD；123456由意知，题AB，AD，AP垂直，以两两A坐原点，为标AB，AD，AP所在直分线别为x、轴y、轴z，建立空直角坐系，轴间标如，图平面设PBD的法向量为n＝(x，y，z)，设PA＝AB＝2，则P(0,0,2)，B(2,0,0)，D(0,2,0)，C(2,2,0)，M(1,1,1)，PB→＝(2,0，－2)，PD→＝(0,2，－2)，AM→＝(1,1,1)，则n·PB→＝2x－2z＝0，n·PD→＝2y－2z＝0，取x＝1，得n＝(1,1,1)， AM→＝n，∴AM⊥平面PBD.(2)直设线AM平面与PBD交于O，求：证AO＝2OM.123456123456如，接图连AC交BD于点E，则E是AC的中点，接连PE， AM∩平面PBD＝O，∴O∈AM且O∈平面PBD， AM⊂平面PAC，∴O∈平面PAC，又平面PBD∩平面PAC＝PE，∴O∈PE，123456∴AM，PE的交点就是O，接连ME， M是PC的中点，∴PA∥ME，PA＝2ME，∴△PAO∽△EMO，∴AO＝2OM.∴PAME＝AOOM＝21，1234563.如，在四图棱锥P－ABCD中，PA⊥平面ABCD，AB∥CD，PA＝AB＝2CD＝2，∠ADC＝90°，E，F分别为PB，AB的中点.(1)求：证CE∥平面PAD；123456接连EF(略图)， E，F分别为PB，AB的中点，∴EF∥PA， EF⊄平面PAD，PA⊂平面PAD，∴EF∥平面PAD， AB∥CD，AB＝2CD，∴AF∥CD，且AF＝CD.∴四形边ADCF平行四形，即为边CF∥AD， CF⊄平面PAD，AD⊂平面PAD，∴CF∥平面PAD， EF∩CF＝F，EF，CF⊂平面EFC，∴平面PAD∥平面EFC，CE⊂平面EFC，则CE∥平面PAD.123456(2)求点B到平面PCF的距离.123456 ∠ADC＝90°，AB∥CD，∴AB⊥AD，CF⊥AB，又PA⊥平面ABCD，∴PA⊥CF，又PA∩AB＝A，∴CF⊥平面PAB，∴CF⊥PF.设CF＝x，则S△AFC＝12×1×x＝x2，S△PFC＝12×5×x＝52x，点设A到平面PCF的距离为h，由VP－AFC＝VA－PFC，得13×x2×2＝13×5x2×h，则h＝255.123456 点F为AB的中点，∴点B到平面PCF的距离等于点A到平面PCF的距离，为255.1234564.(2022·全乙卷国)如，四面体图ABCD中，AD⊥CD，AD＝CD，∠ADB＝∠BDC，E为AC的中点.(1)明：平面证BED⊥平面ACD；123456因为AD＝CD，E为AC的中点，所以AC⊥DE.在△ADB和△CDB中，因为AD＝CD，∠ADB＝∠CDB，DB＝DB，所以△ADB≌△CDB，所以AB＝BC.因为E为AC的中点，所以AC⊥BE.又BE∩DE＝E，BE，DE⊂平面BED，所以AC⊥平面BED，又AC⊂平面ACD，所以平面BED⊥平面ACD.123456(2)设AB＝BD＝2，∠ACB＝60°，点F在BD上，当△AFC的面积最小，求时CF平面与ABD所...