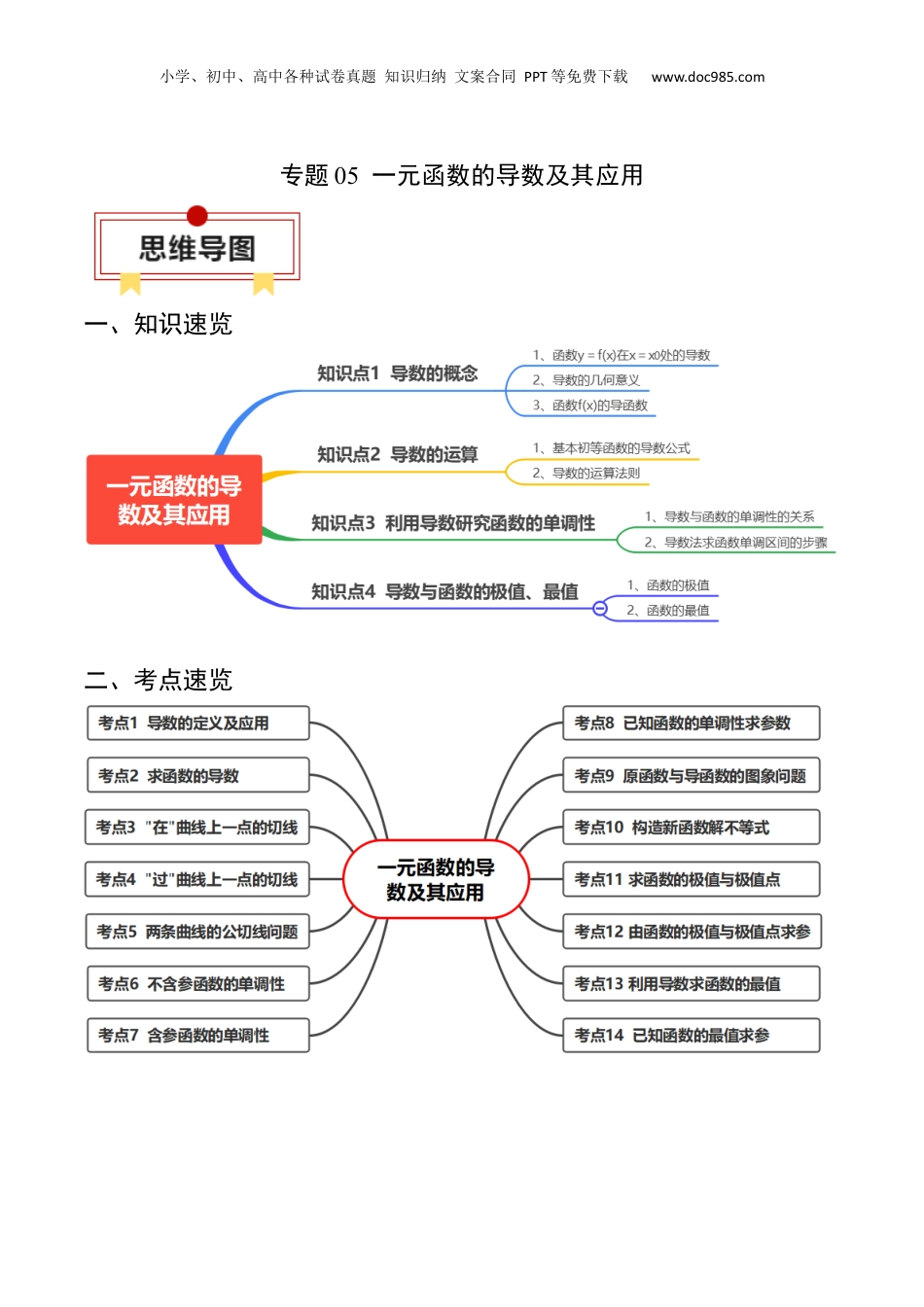
小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com专题05一元函数的导数及其应用一、知识速览二、考点速览小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com知识点1导数的概念1、函数y＝f(x)在x＝x0处的导数一般地，称函数y＝f(x)在x＝x0处的瞬时变化率＝lim为函数y＝f(x)在x＝x0处的导数，记作f′(x0)或y′|x＝x0，即f′(x0)＝lim＝lim．2、导数的几何意义函数f(x)在点x0处的导数f′(x0)的几何意义是在曲线y＝f(x)上点P(x0，y0)处的切线的斜率(瞬时速度就是位移函数s(t)对时间t的导数)．相应地，切线方程为y－y0＝f′(x0)(x－x0)．3、函数f(x)的导函数：称函数f′(x)＝lim为f(x)的导函数．知识点2导数的运算1、基本初等函数的导数公式原函数导函数f(x)＝c(c为常数)f′(x)＝0f(x)＝xn(n∈Q*)f′(x)＝nxn－1f(x)＝sinxf′(x)＝cos_xf(x)＝cosxf′(x)＝－sin_xf(x)＝ax(a>0且a≠1)f′(x)＝axln_af(x)＝exf′(x)＝exf(x)＝logax(x>0，a>0且a≠1)f′(x)＝f(x)＝lnx(x>0)f′(x)＝2、导数的运算法则(1)[f(x)±g(x)]′＝f′(x)±g′(x)．(2)[f(x)·g(x)]′＝f′(x)g(x)＋f(x)g′(x)．(3)′＝(g(x)≠0)．知识点3利用导数研究函数的单调性1、导数与函数的单调性的关系在某个区间内，如果，那么函数在这个区间内单调递增；如果，那么函数在这个区间内单调递减．【注意】（1）在某区间内（）是函数在此区间上为增（减）函数的充分不必要条件；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com（2）可导函数在上是增(减)函数的充要条件是对∀x∈(a，b)，都有（）且在上的任何子区间内都不恒为零．2、导数法求函数单调区间的步骤（1）确定函数fx的定义域；（2）求fx（通分合并、因式分解）；（3）解不等式0fx，解集在定义域内的部分为单调递增区间；（4）解不等式0fx，解集在定义域内的部分为单调递减区间．知识点4导数与函数的极值、最值1、函数的极值（1）函数的极小值：函数y＝f(x)在点x＝a的函数值f(a)比它在点x＝a附近其他点的函数值都小，f′(a)＝0；而且在点x＝a附近的左侧f′(x)＜0，右侧f′(x)＞0，则点a叫做函数y＝f(x)的极小值点，f(a)叫做函数y＝f(x)的极小值．（2）函数的极大值：函数y＝f(x)在点x＝b的函数值f(b)比它在点x＝b附近其他点的函数值都大，f′(b)＝0；而且在点x＝b附近的左侧f′(x)＞0，右侧f′(x)＜0，则点b叫做函数y＝f(x)的极大值点，f(b)叫做函数y＝f(x)的极大值．2、函数的最值（1）在闭区间[a，b]上连续的函数f(x)在[a，b]上必有最大值与最小值．（2）若函数f(x)在[a，b]上单调递增，则f(a)为函数的最小值，f(b)为函数的最大值；若函数f(x)在[a，b]上单调递减，则f(a)为函数的最大值，f(b)为函数的最小值．一、求曲线“在”与“过”某点的切线1、求曲线“在”某点处的切线方程步骤第一步（求斜率）：求出曲线在点00,xfx处切线的斜率0()fx第二步（写方程）：用点斜式000()()()yfxfxxx第三步（变形式）：将点斜式变成一般式。2、求曲线“过”某点处的切线方程步骤第一步：设切点为00,Qxfx；小学、初中、高中各种试卷真题知识归纳文案合同PPT等免费下载www.doc985.com第二步：求出函数()yfx在点0x处的导数0()fx；第三步：利用Q在曲线上和0()PQfxk，解出0x及0()fx；第四步：根据直线的点斜式方程，得切线方程为000()()()yfxfxxx．【典例1】（2023·陕西西安·西安市大明宫中学校考模拟预测）已知函数，则曲线在点处的切线方程为（）A．B．C．D．【典例2】（2023·西藏日喀则·统考一模）已知直线是曲线在点处的切线方程，则【典例3】（2023·云南·校联考模拟预测）曲线过坐标原点的切线方程为.【典例4】（2023·陕西宝鸡·统考二模）若过点可作曲线的三条切线，则的取值范围是（）A．B．C．D．二、含参函数单调性讨论依据（1）导函数有无零点讨论（或零点有无意义）；（2）导函数的零点在不在定义域或区间内；（3）导函数多个零点时大小的讨论。【典例1】（2023·全国·高三对口高考）已知函数，求函数的单调区...